Proposition 11: To draw a straight line at right angles to a given straight line from a given point on it.

Proof.
Let this straight line be $AB$ and the given point be $C$.

Let a point $D$ be taken at random on the line $AB$.

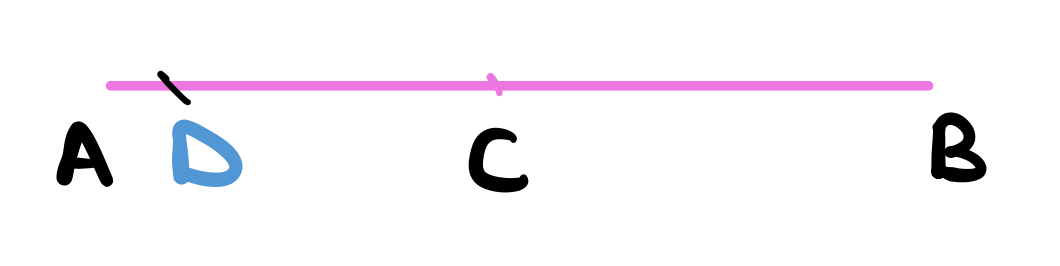
Use proposition 3 to cut a line equal to $CE$ equal to $CD$.

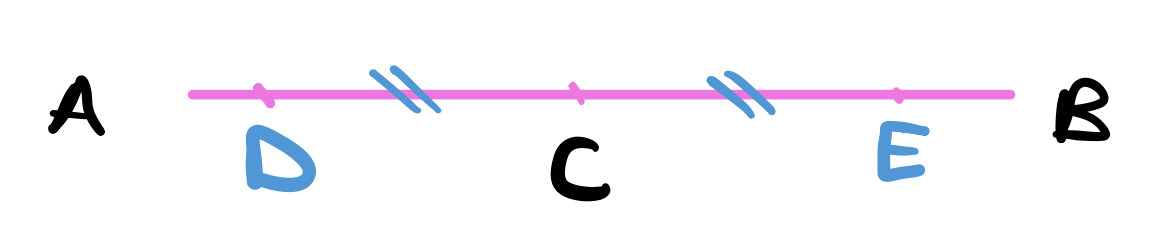
Use proposition 1 to construct an equilaterals triangle from the base $DE$.

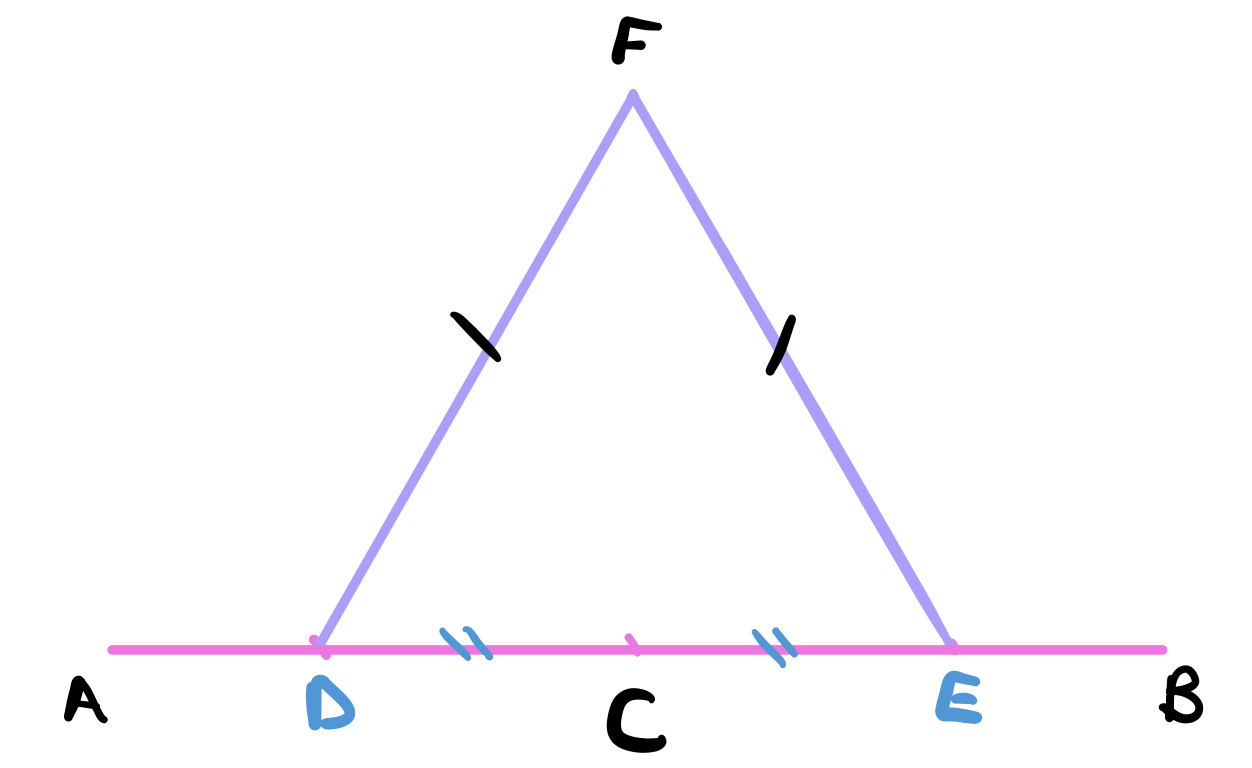
Draw a straight line between the points $C$ and $F$ using postulate 1

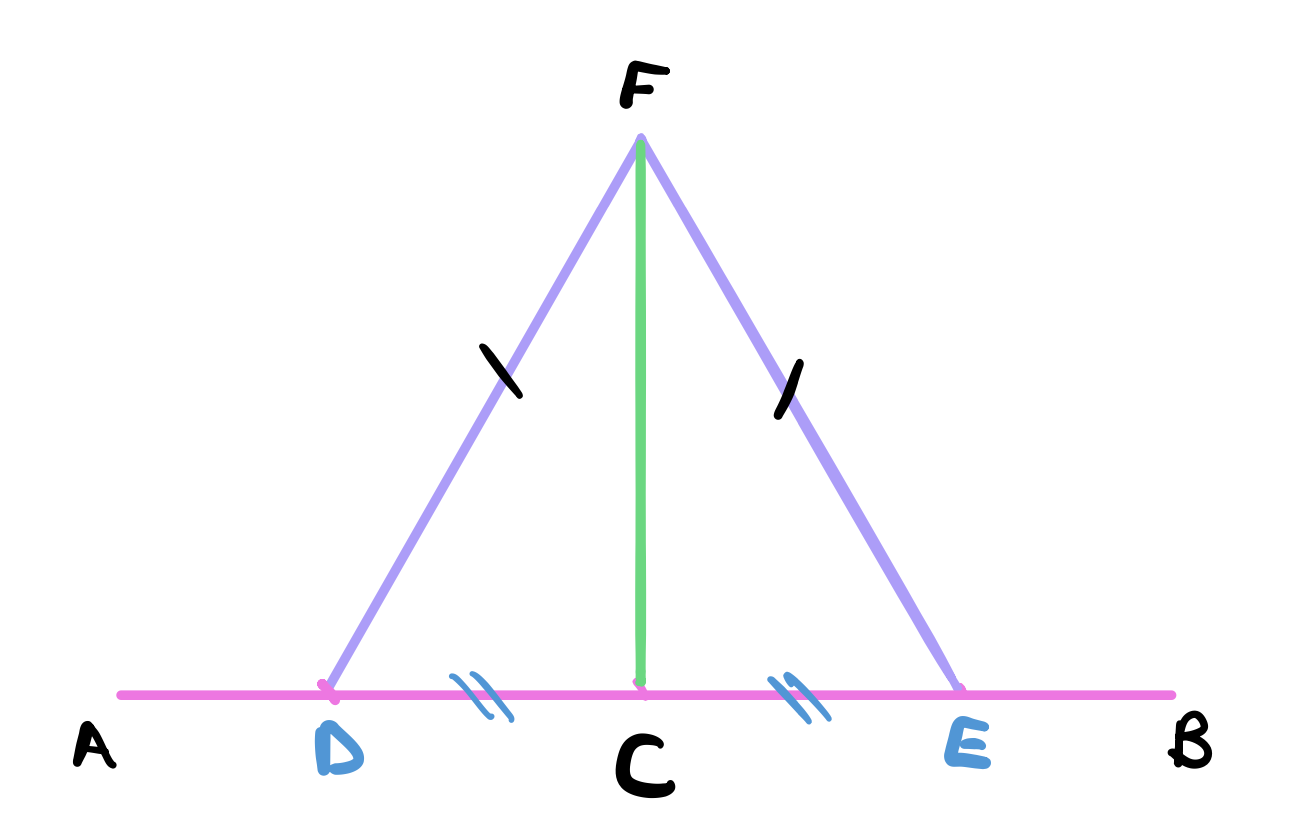
The claim is that the line $FC$ has been drawn at right angles to the given line $AB$.

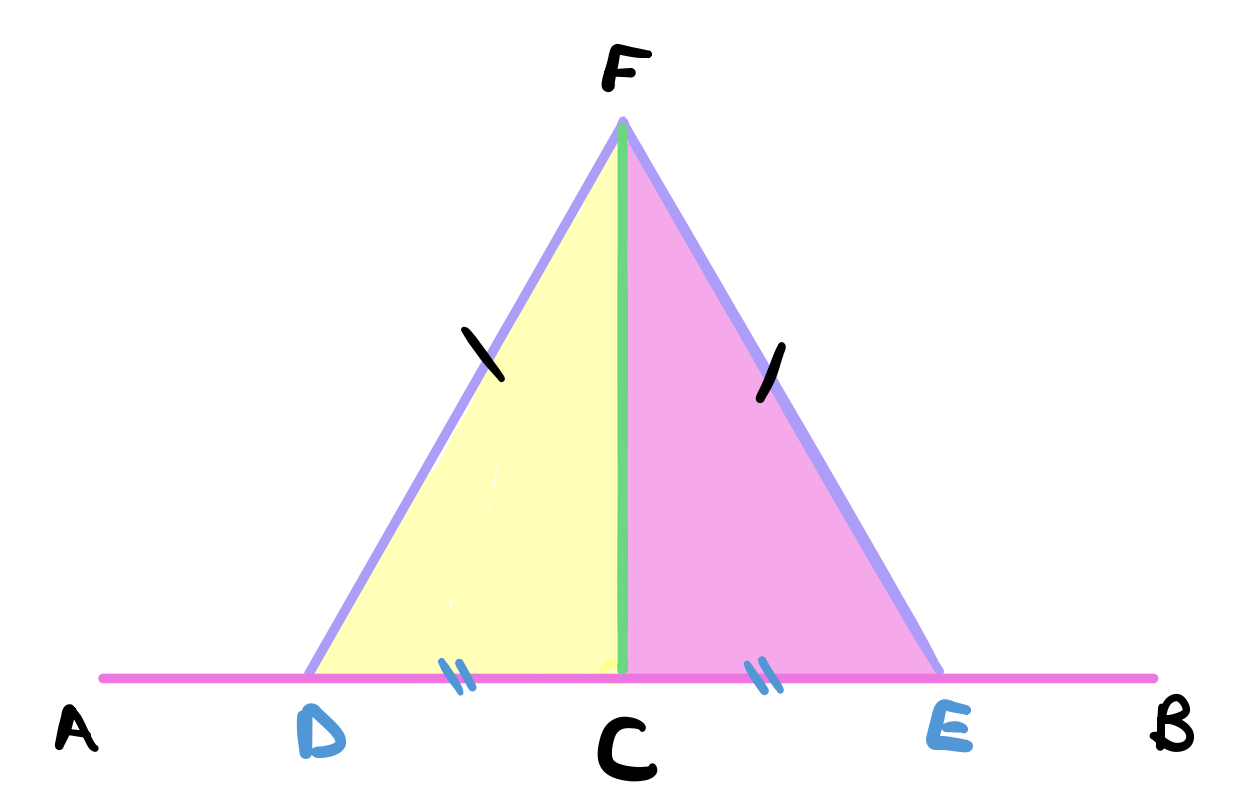
To see this, notice that in the triangles $FDC$ and $FCE$, the side $FC$ is a common side. $FD=FE$ and $DC = CE$ by construction. Therefore, we conclude by proposition 8 that the angles $\angle FCD$ and $\angle FCE$ are equal.

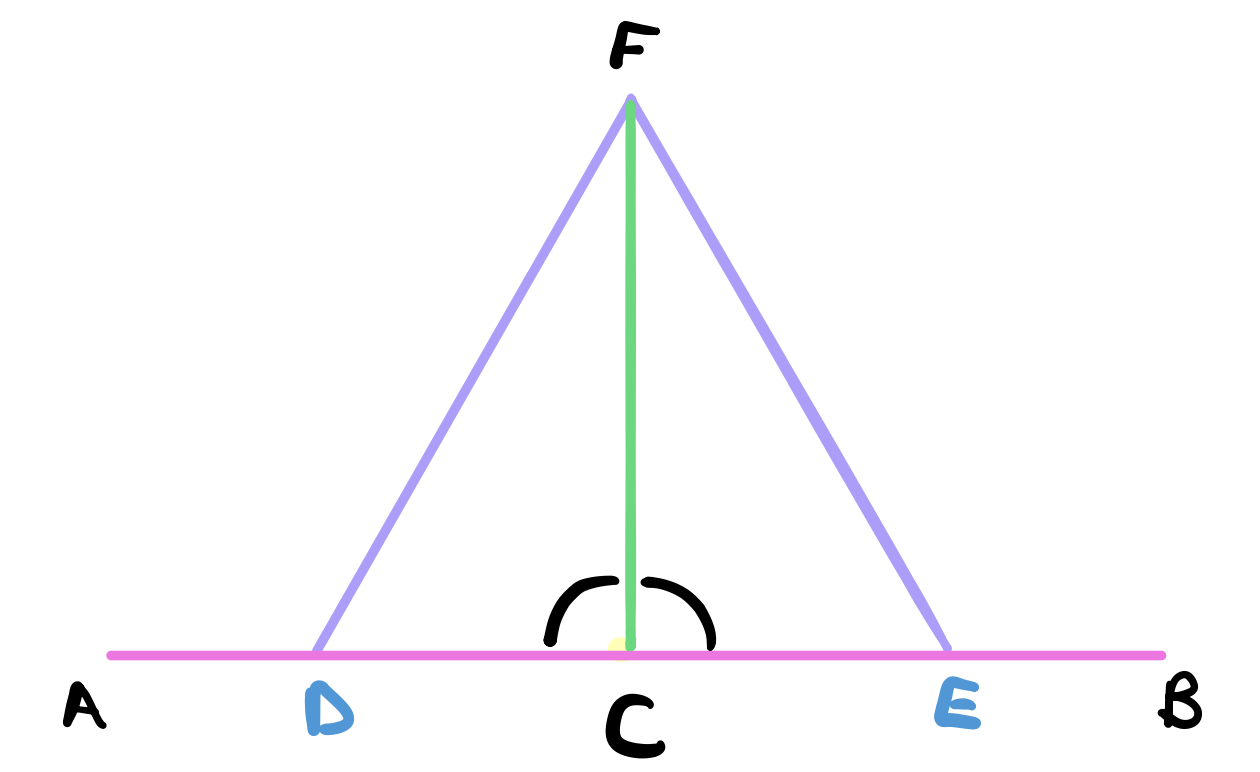
Recall that definition 10. says that if we have a straight line set up on a straight line such that the adjacent angles are equal to each other then each of the equal angles is right. Therefore we can conclude that the angles $\angle FCD$ and $\angle FCE$ are both right and so the drawn line $FC$ is drawn at right angles to the given line $AB$ as required.

Thoughts: -