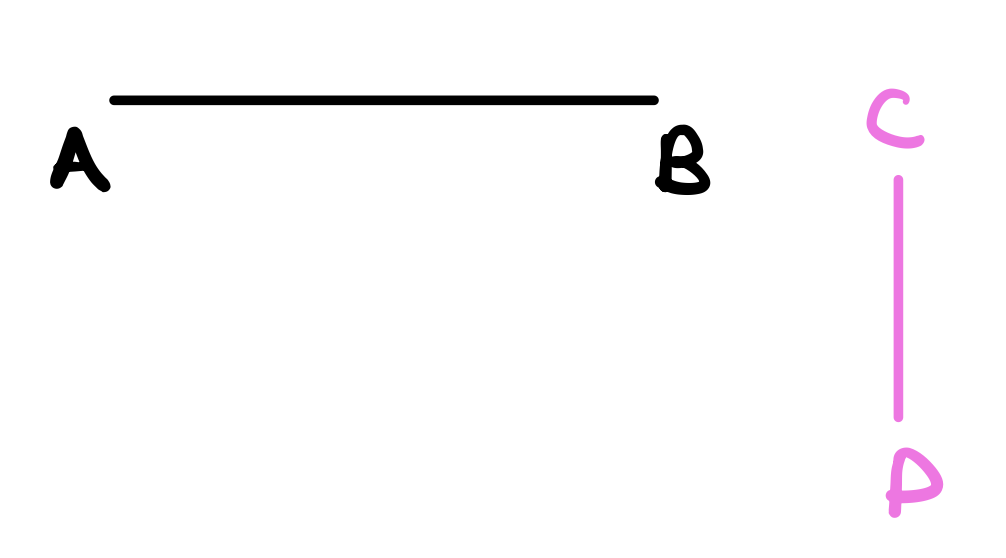
Proposition 3: “To cut off from the greater of two given unequal straight lines a straight line equal to the less.” In other words, given two unqual lines. Let \(AB\) be the greater one and \(CD\) the smaller one. Cut from \(AB\) a line equal to \(CD\).
Proof.
Let the greater line be \(AB\) and the smaller line be \(CD\).
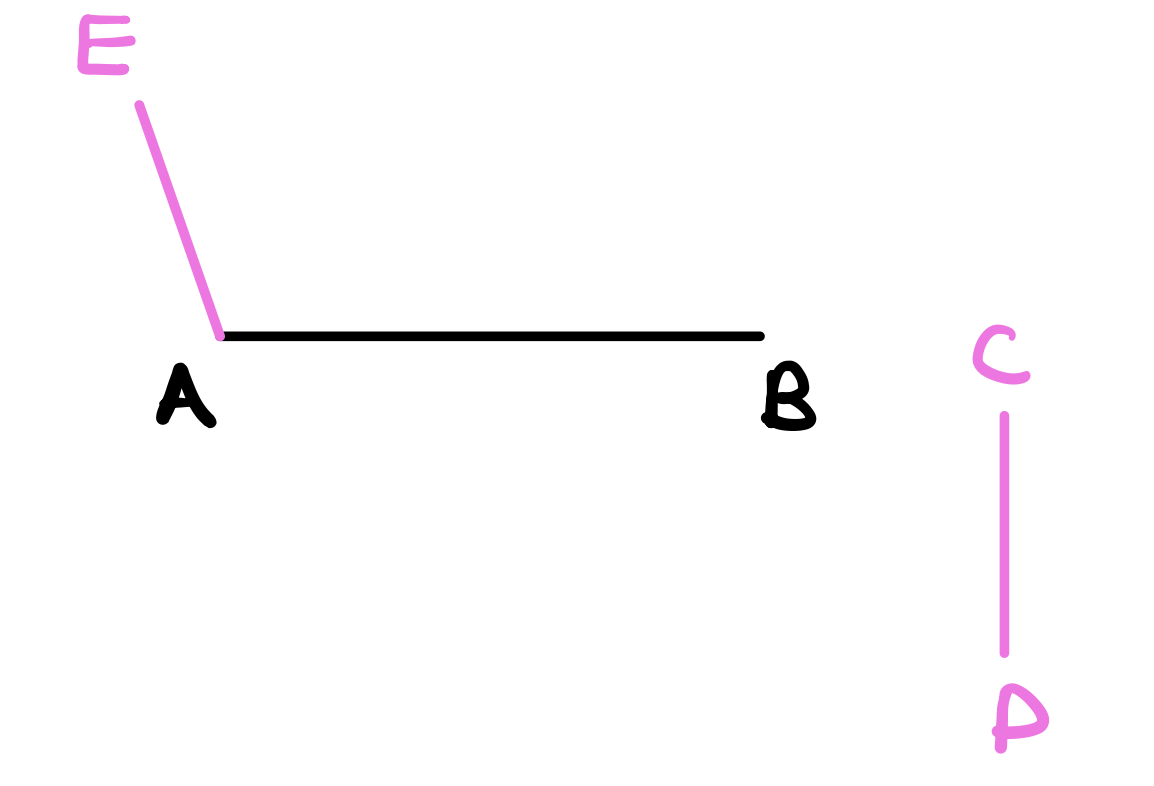
Use proposition 2 to describe a line starting at \(A\) that is equal in length to line \(CD\).
Now, describe a circle with center at point \(A\) and radius of length \(AE\) using postulate 3.
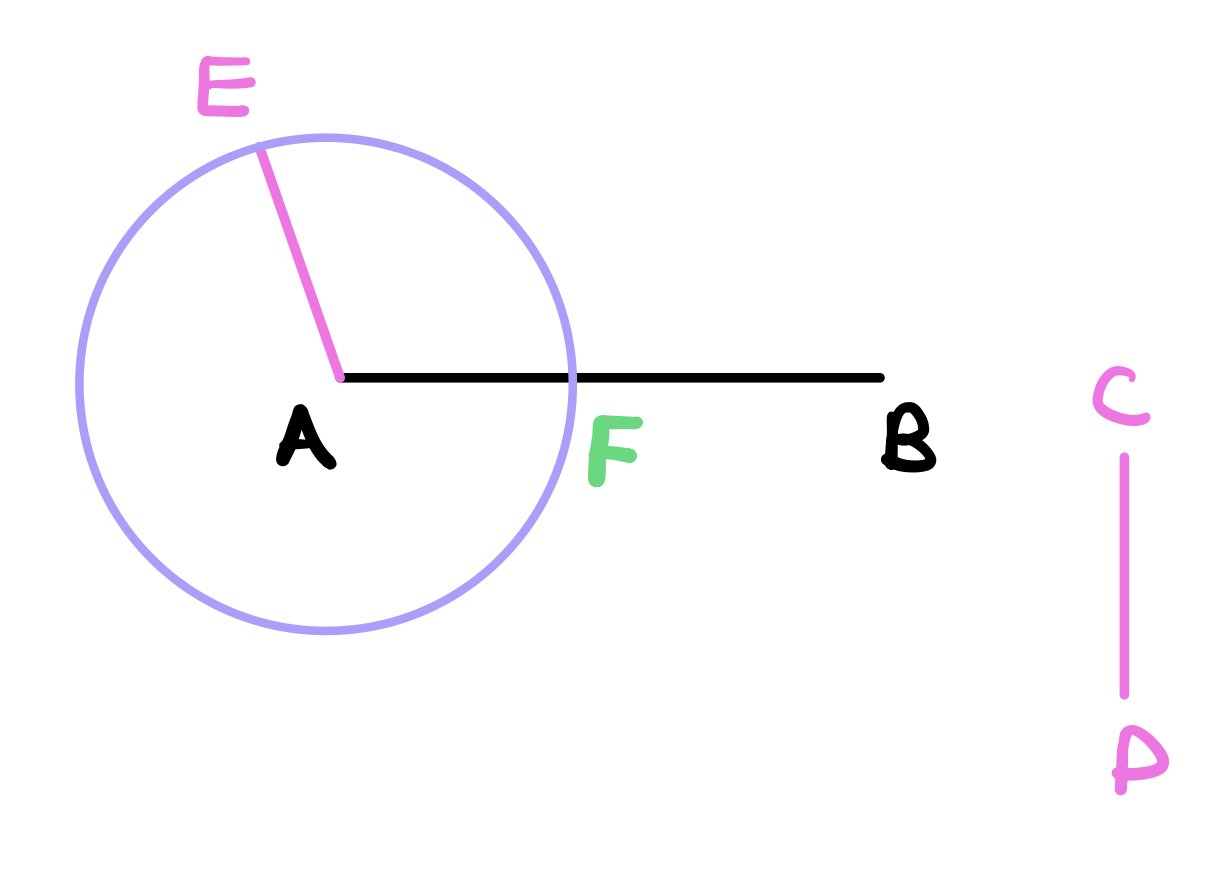
The claim is that \(AF\) is equal to \(CD\). To see this, we know that \(EA = AF\) by definition 15. We also know that \(EA = CD\) by construction. Therefore \(AF = CD\) by axiom 1 (Magnitudes which are equal to the same are equal to each other).
Thoughts: I guess we wanted to prove that we can cut up a line such that a portion of that line is equal to a given line. I’m very early in the book and not sure where I see this is going.
References: