Proposition 2: “From a given point, to draw a straight line equal to a given finite straight line”. In other words, given a point \(A\) and another finite straight line \(CB\), draw a line equal to \(CB\) at \(A\).
Proof.
Let the given point be \(A\) and the given finite line be \(CB\).
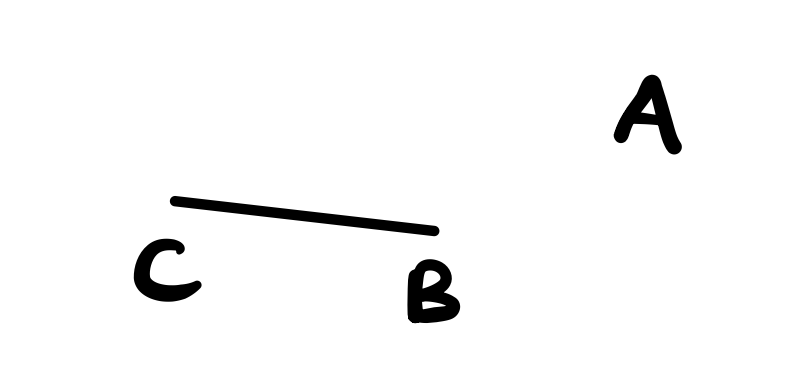
Use postule 1 to draw a line between \(A\) and one of the end points say \(B\).
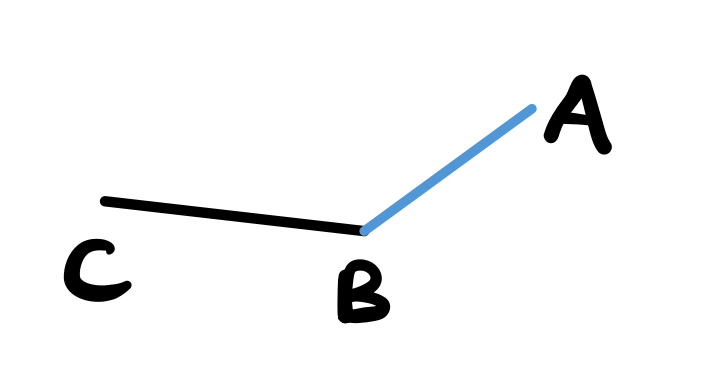
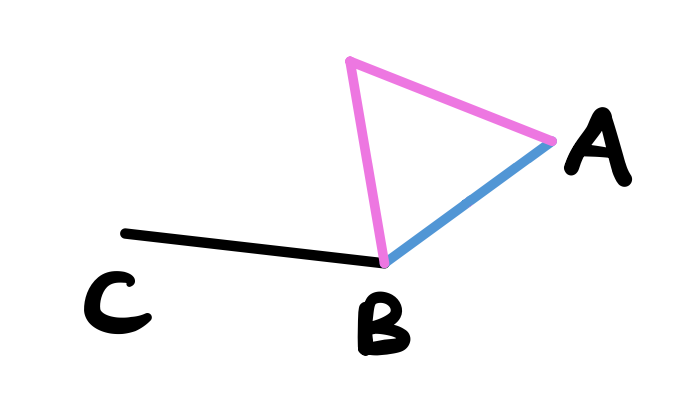
Next, use proposition 1 to draw an equilateral triangle from the drawn line \(AB\).
Next, describe a circle with center \(B\) and radius \(CB\) using postulate 3
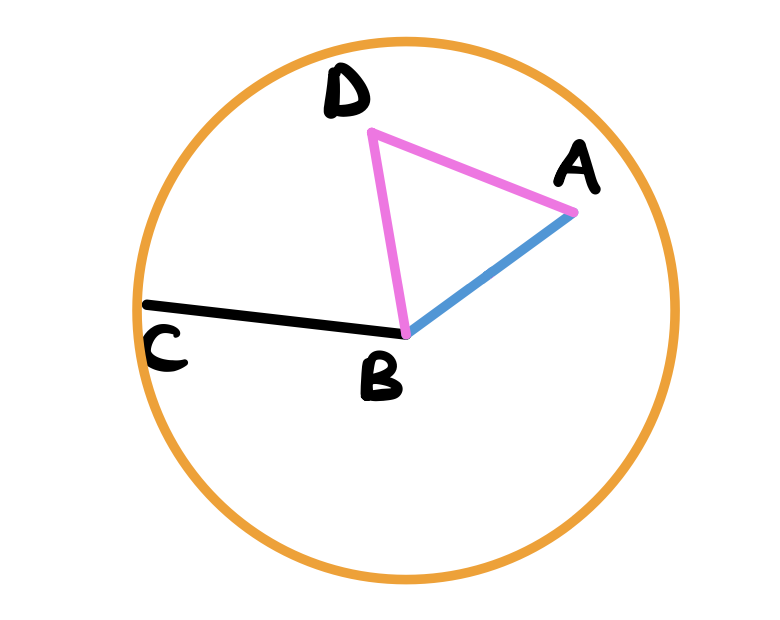
Extend the line DB all the way till intersects the circle at \(E\) using postulate 2.
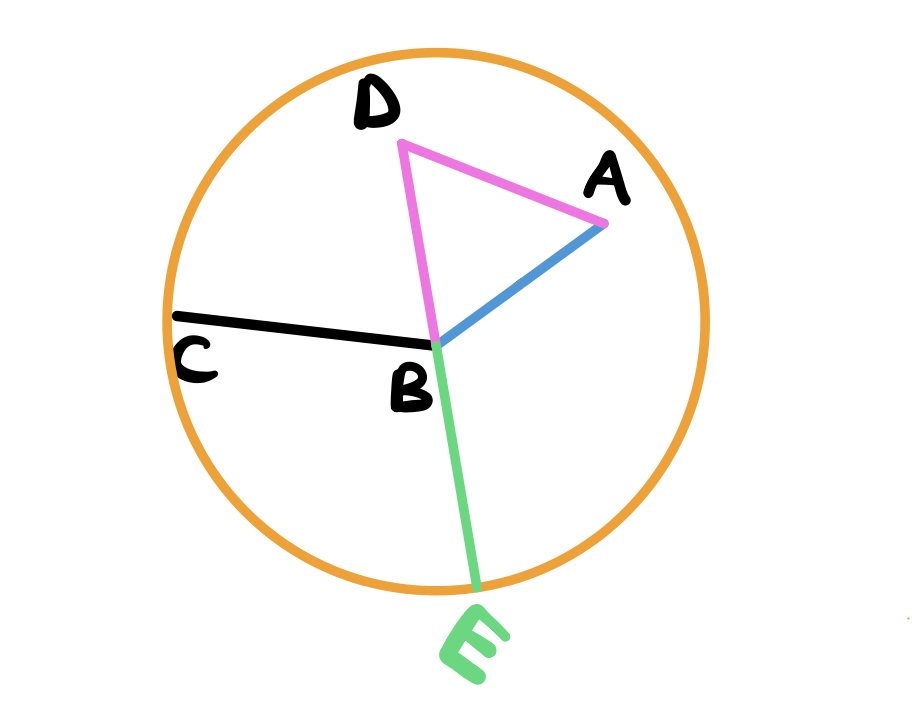
Now describe another circle with center \(D\) and radius \(DE\) (postulate 3).
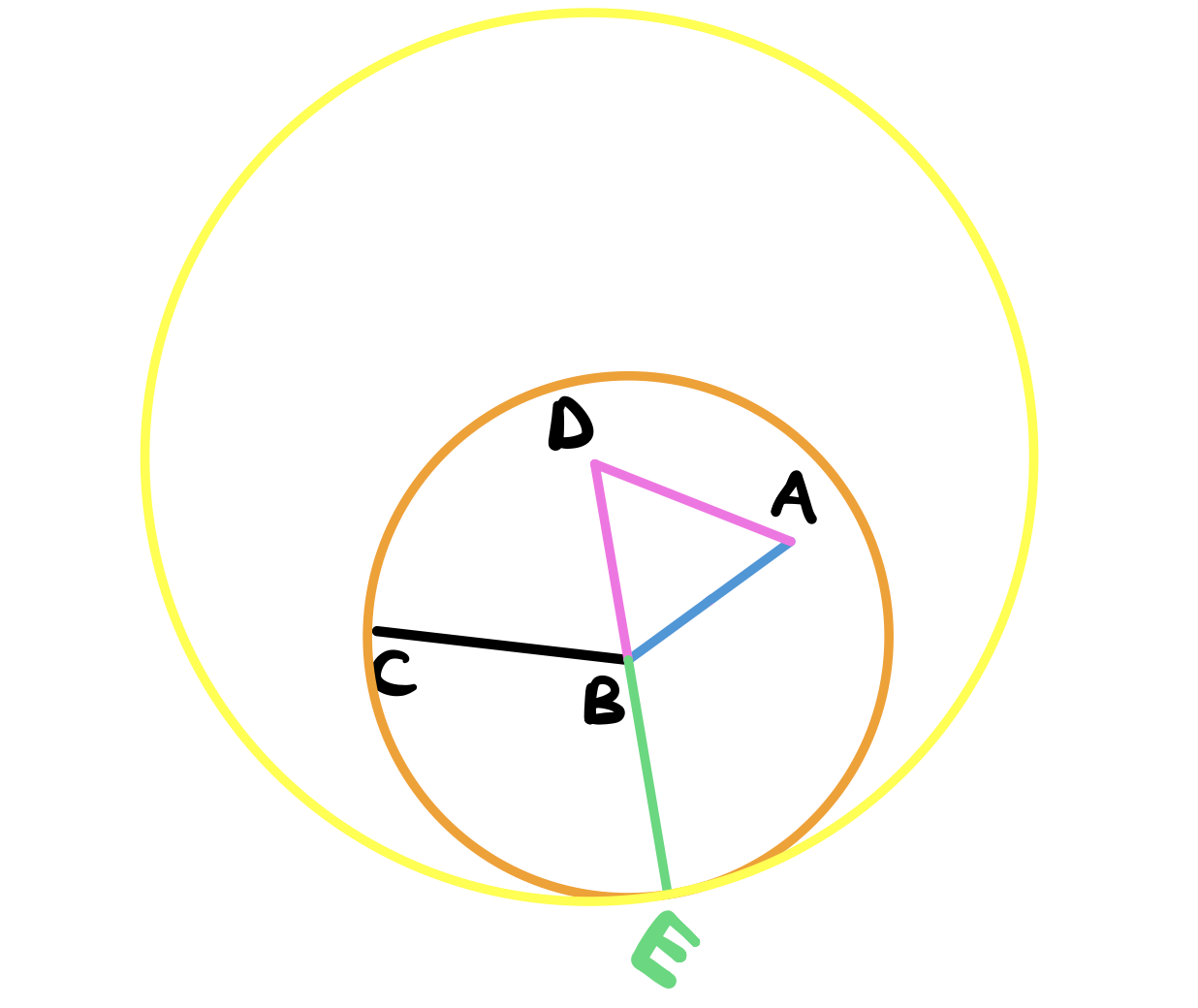
Extend the line DA until it intersects the circle at \(F\).
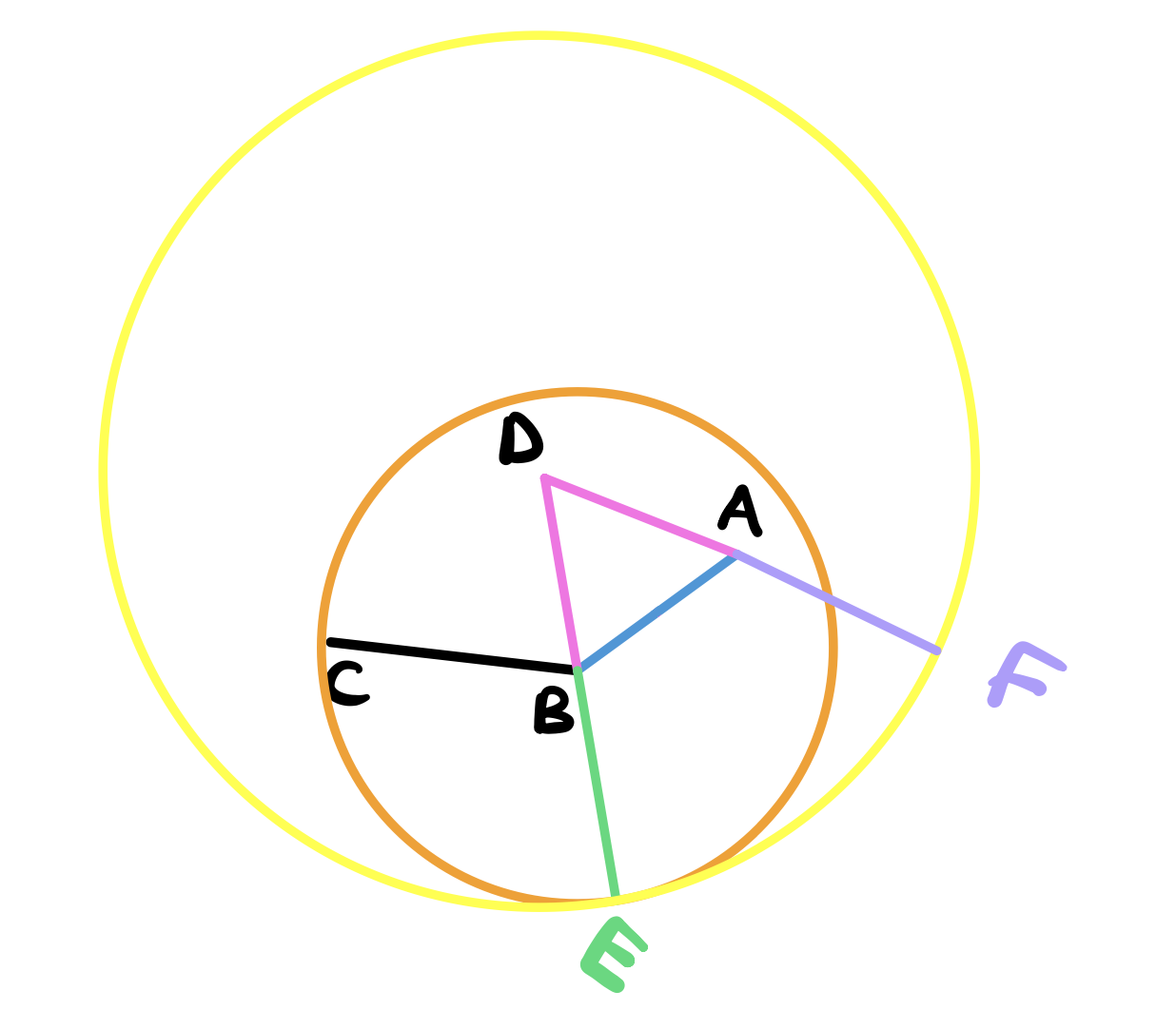
The claim is that \(AF = BC\) which is what we want. To see this, we know that \(DF=DE\) by definition 15. We know that \(DA = DB\) by construction. Therefore, \(BE = AF\) by common notion 3. But \(CB = BE\) by definition 15 and so \(CB = AF\) (common notion 3) as required.
References: