Proposition 1: To construct an equilateral triangle on a given finite straight line.
Proof.
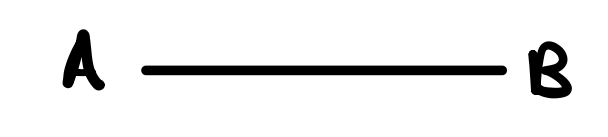
Let the finit straight line be \(AB\) above. By postulate 3, describe a cricle with center \(A\).
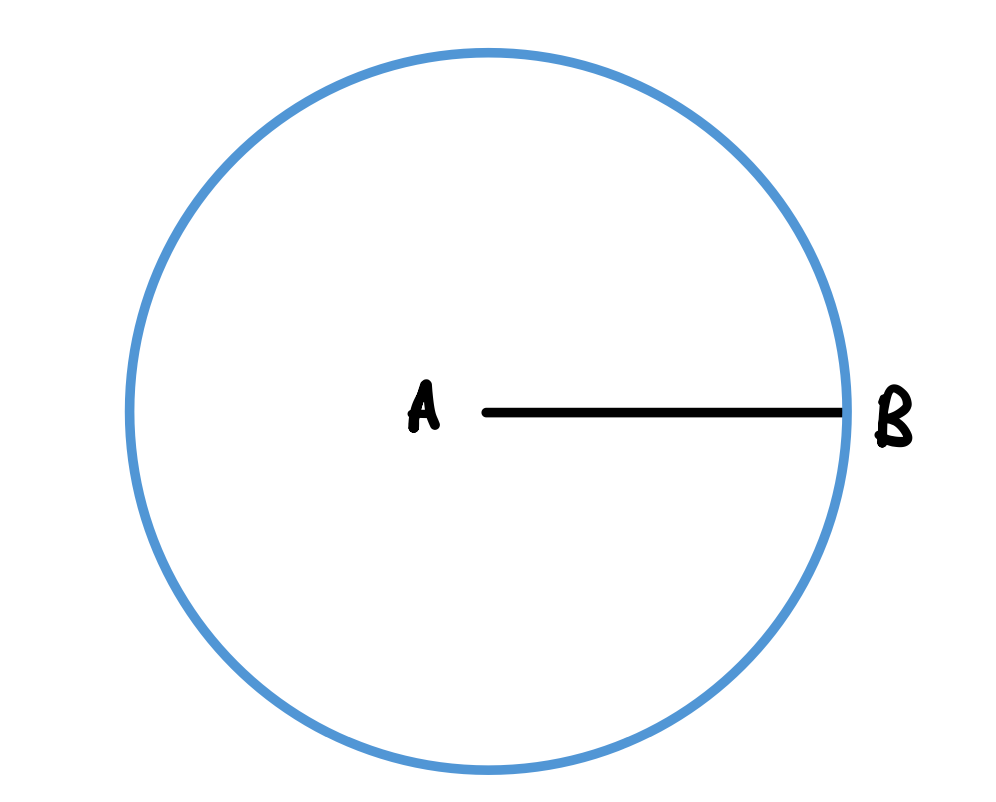
By postulate 3, describe another circle with center \(B\).
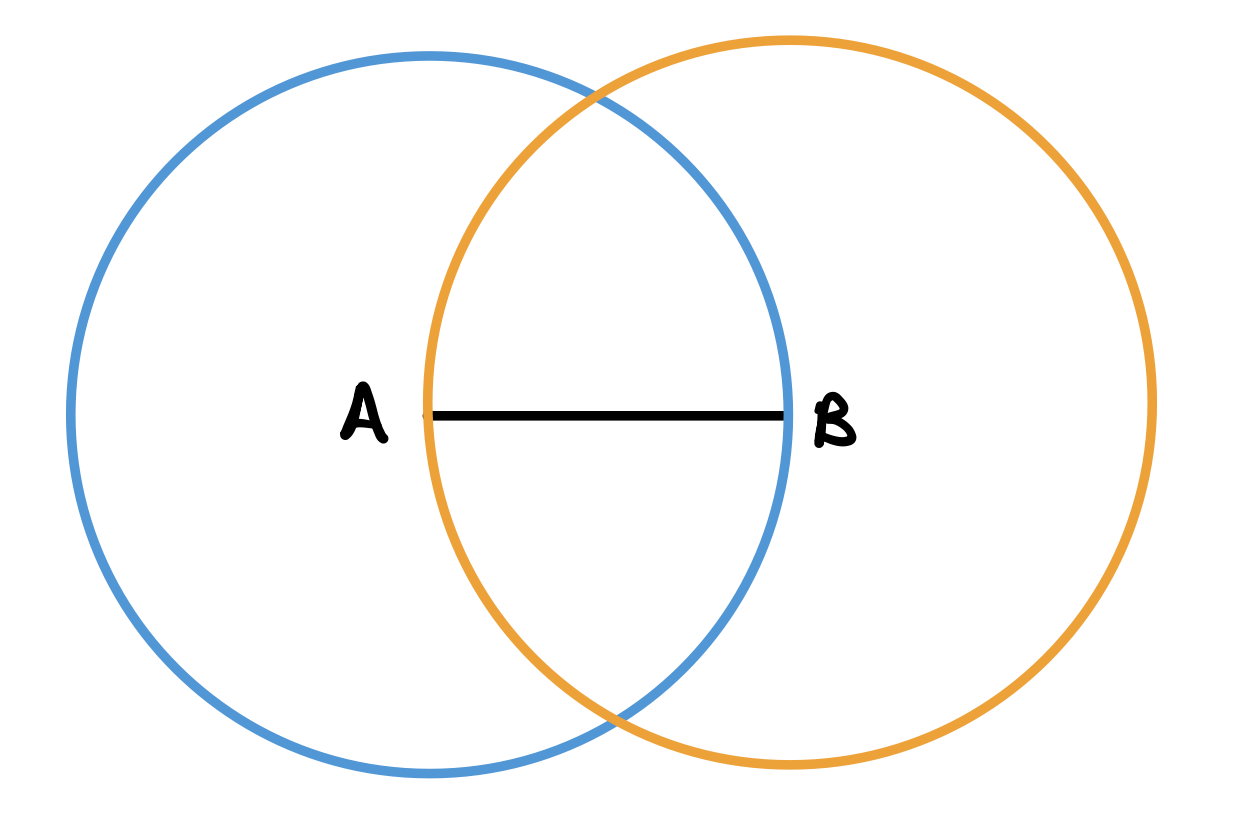
Using postulate 1, draw two lines from \(A\) and from \(B\) to point \(C\) (the intersection of the two circles).
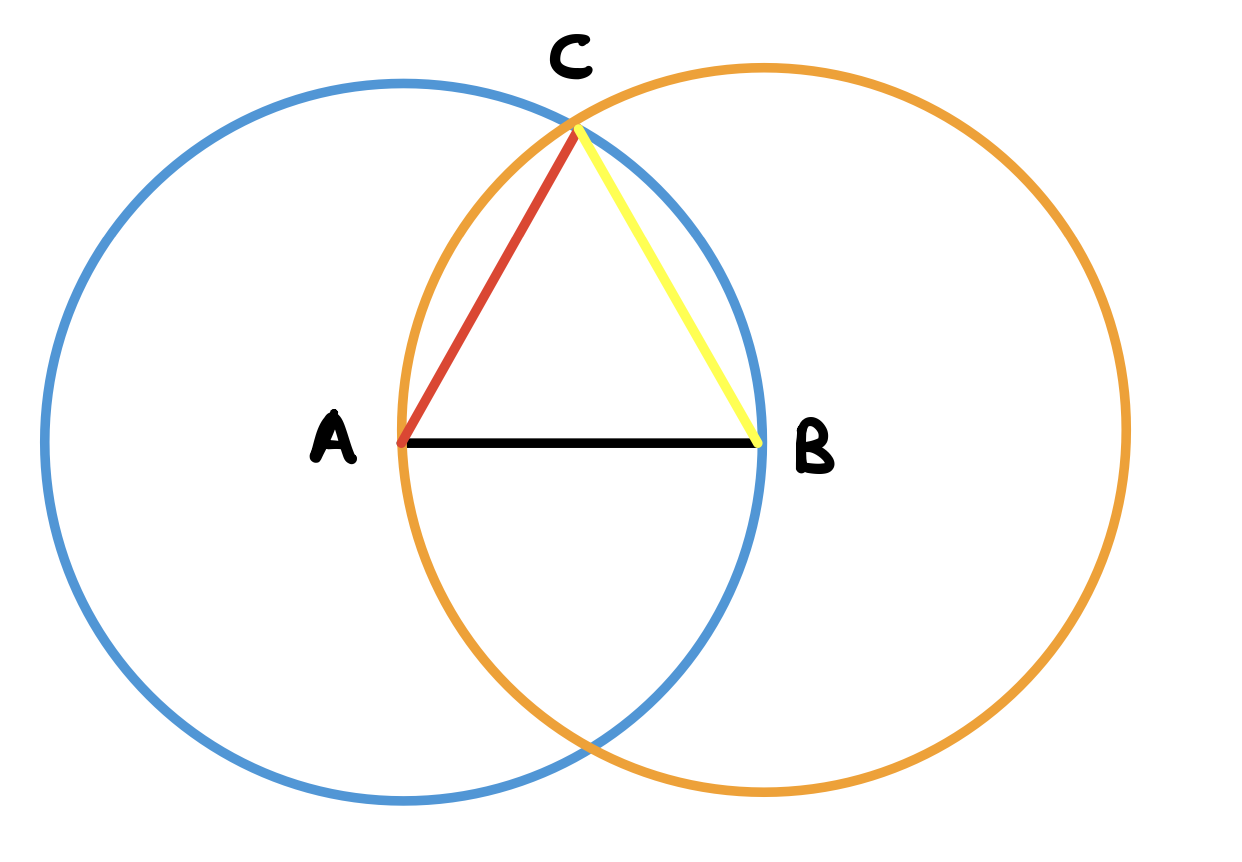
We know that \(AB = AC\) and \(AB = BC\) by definition 15. Therefore, \(BC = AC\) by common notion 1. We see now that \(AB = BC = AC\) and therefore the triangle is equaliteral as required.
References: