Proposition 8: “If two triangles have the two sides equal to two sides respectively, and have also the base equal to the base, they will also have the angles equal which are contained by the equal straight lines.”

Proof.

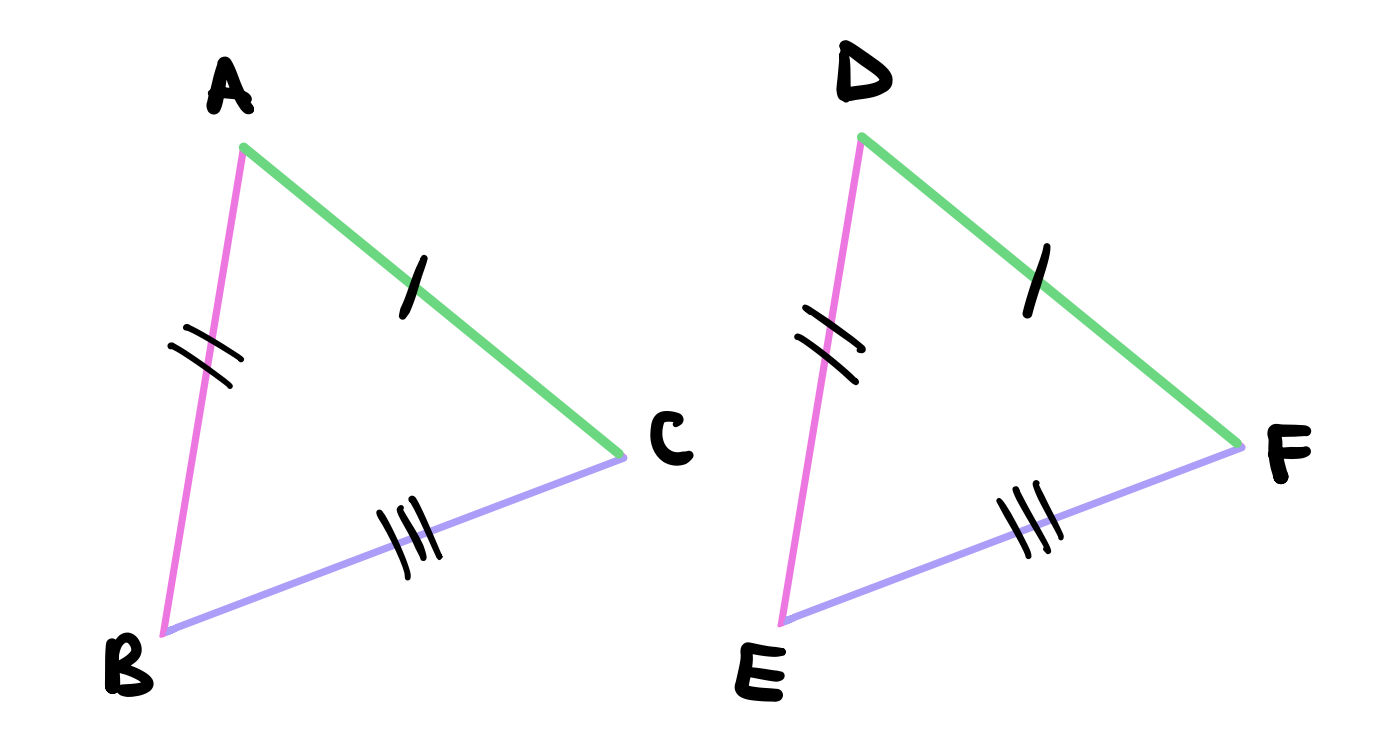
Let the triangles be \(ABC\) and \(DEF\) respectively. Let \(AB = DE\), \(AC = DF\) and the bases \(BC = EF\). We will prove that the angle \(\angle BAC\) equals the angle \(\angle EDF\).

Using proposition 2, copy the triangle \(DEF\) to where the triangle \(ABC\) is, by placing the vertex \(B\) onto the vertex \(E\) and the straight line \(BC\) on top of the straight line \(EF\). The point \(C\) must coincide with the point \(F\) since we have \(BC = EF\) by our hypothesis.

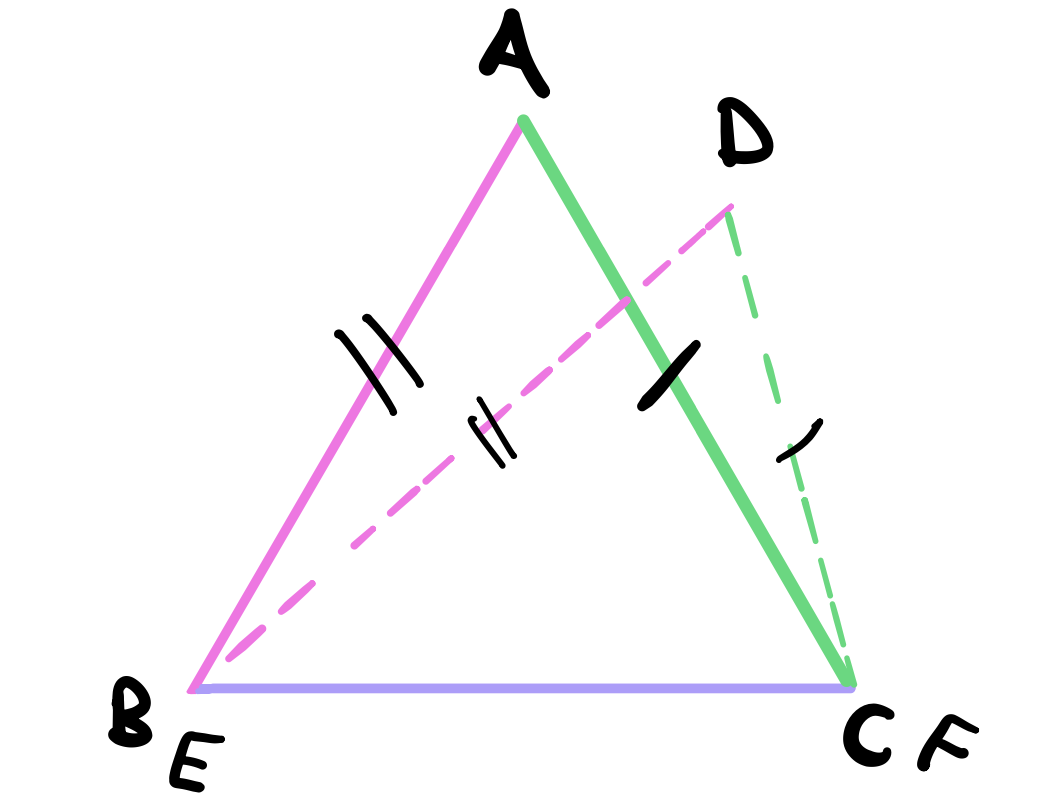
We claim that \(AB\) must coincide with \(DE\) and \(AC\) must coincide with \(DF\). To see this, recall that \(AB = DE\) and \(AC = DF\) by our hypothesis. Since we have the same base and the lines are equal, then we can use proposition 7 to conclude that the lines \(DE\) and \(DF\) must meet where the lines \(AB\) and \(AC\) meet which is point \(A\). Therefore, we see that point \(D\) must coincide with point \(A\). Therefore, we see that all points coincide with each other and therefore the triangles are equal (really?). Consequently, all angles are equal to each other.

Thoughts: This was messy similar to proposition 4.
(1) Even though the point \(D\) coincided with point \(A\). Why is it necessary for the line \(AB\) to coincide with line \(DE\)? This feels like it needs axiom 10 from Byrne’s book which states that only one straight line can be drawn between two points. right?

(2) If the three points coincide with the other three points, why must the triangles be equal? this feels again like it needs axiom 10.