Proposition 7: “Given two straight lines constructed on a straight line (from its extremities) and meeting in a point, there cannot be constructed on the same straight line (from its extremities), and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each to that which has the same extremity with it.”
In other words, given some finite line \(BC\). If we draw two straight lines from each end point to meet at a point \(A\), then it is not possible to draw another set of straight lines equal to the first set and then have them meet at a different point that \(A\).
Proof.
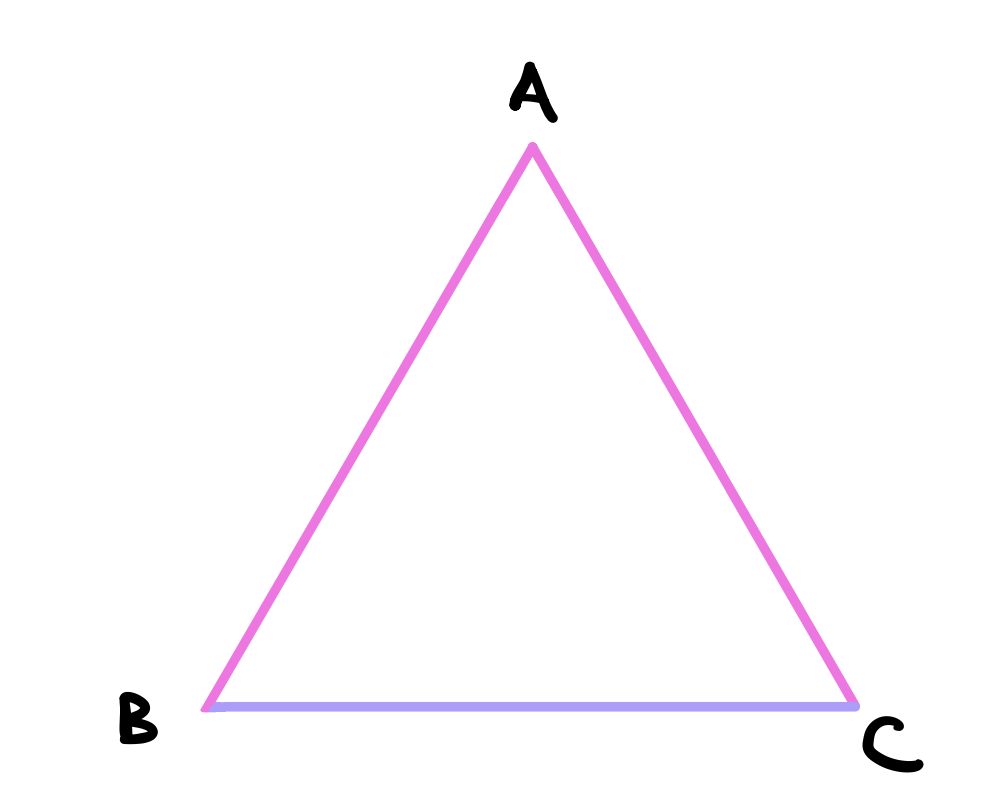
Let the straight lines be \(AB\) and \(AC\) above drawn from the end points of the line \(BC\). Suppose that it is possible to draw another set of lines equal to \(AB\) and \(AC\) and then have the new lines meet at a new point. Let the new point be \(D\) and draw \(DB\) such that it is equal to \(AB\) and draw \(DC\) such that it is equal to \(AC\).
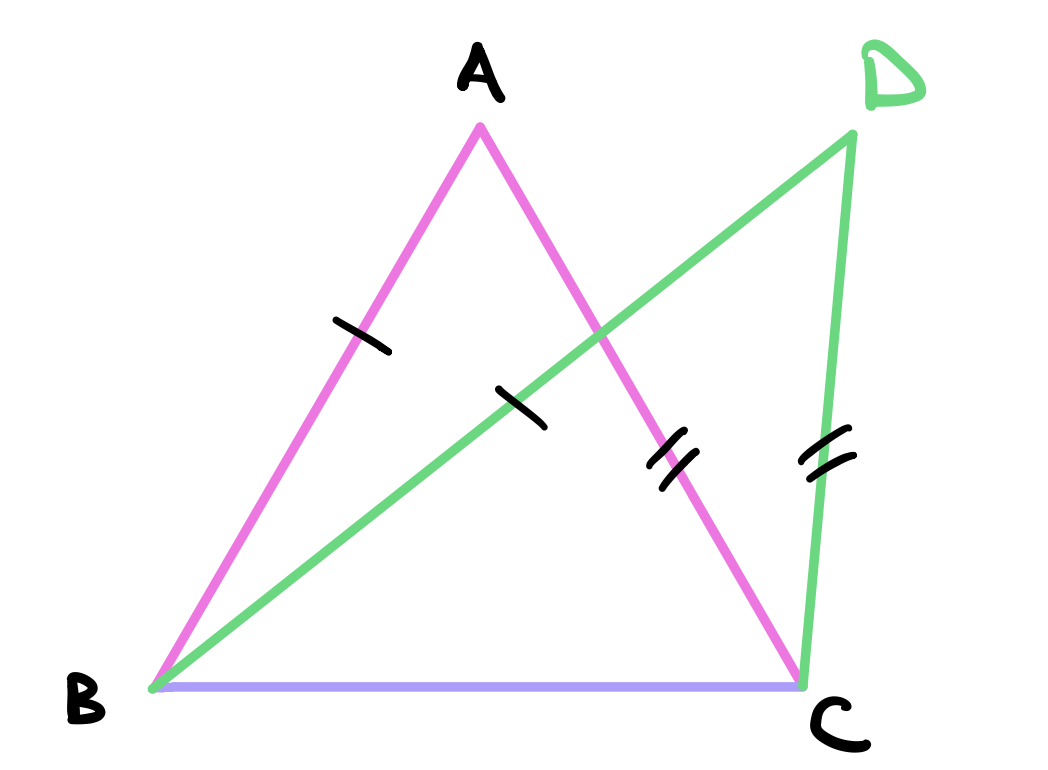
Using postulate 1, draw a line between points \(A\) and \(D\).
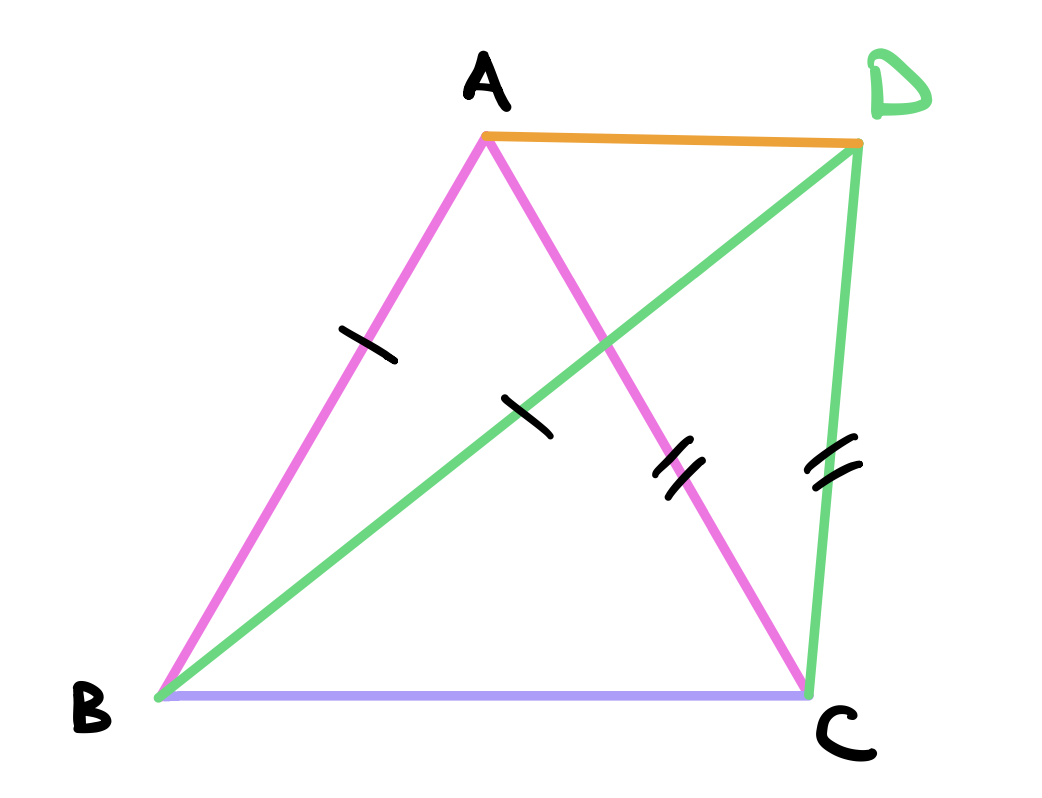
In the triangles \(ABD\), \(AB = DB\) by construction. So \(ABD\) is an isosceles triangle and the angles at the base are equal (proposition 5). Let this angle be \(\alpha\). So \(\angle DAB = \angle ADB = \alpha\). Similarly, the triangle \(ACD\) is also an isosceles triangle by construction and the angles \(\angle DAC\) and \(\angle ADC\) are equal. Let this angle be \(\beta\).
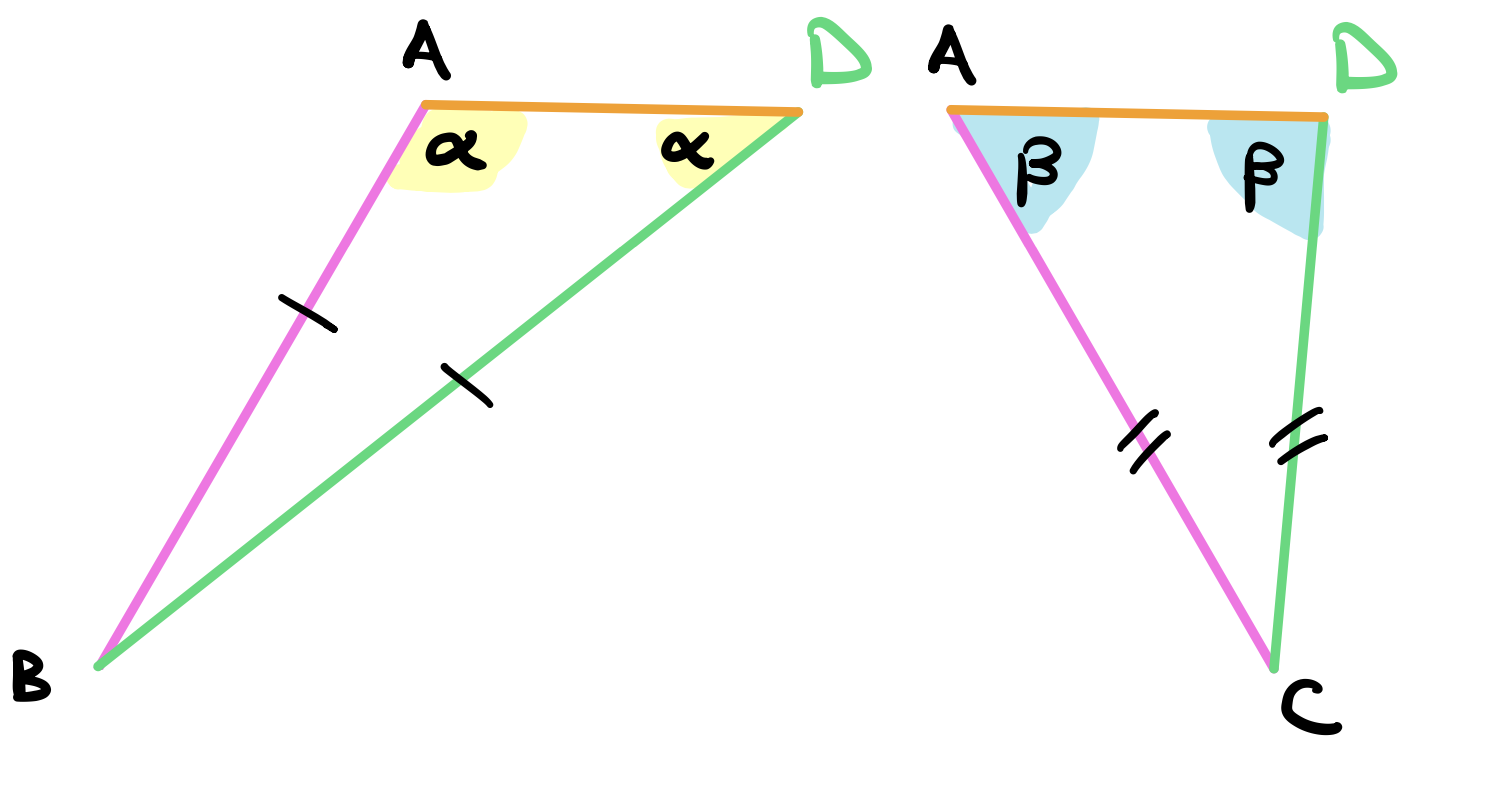
Putting the triangles back together, we know that the angle \(\angle BAD\) is the sum of angles \(\angle BAC\) and \(\angle CAD\). By common notion 5 (The whole is greater than the part.), \(\angle BAD > \angle CAD\). But \(\angle BAD = \alpha\) and \(\angle CAD = \beta\) so \(\alpha > \beta\).
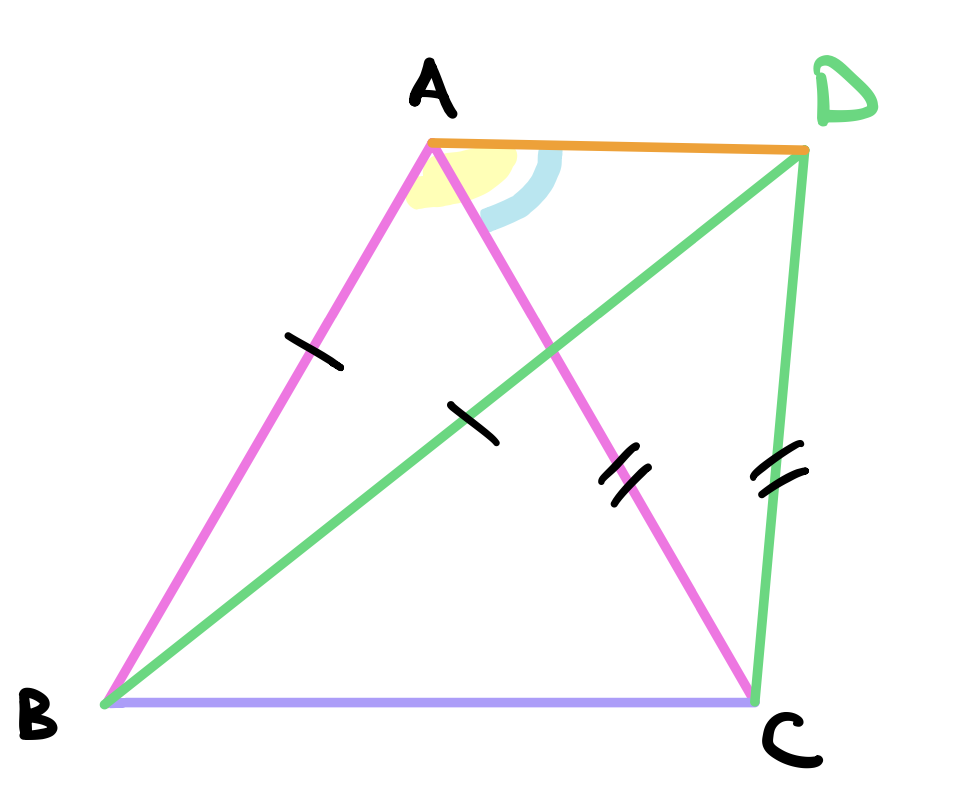
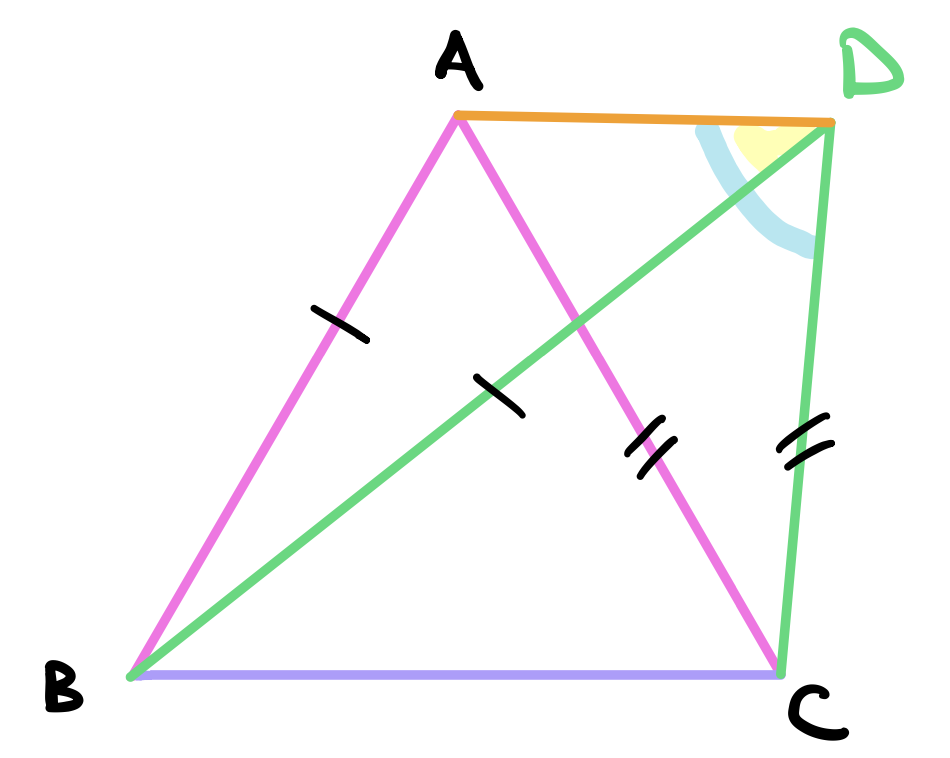
Similarly, the angle \(\angle ADC\) is the sum of angles \(\angle ADB\) and \(\angle BDC\). By common notion 5, \(\angle ADC\) must be greater than \(\angle ADB\). Therefore, \(\beta > \alpha\) which is a contradiction since we said earlier that \(\alpha > \beta\). Therefore, there can not exist two straight lines that are equal to \(AB\) and \(AC\) respectively that meet at a different point than point \(A\).
Thoughts: -
References: