Proposition 10: To bisect a given finite straight line.
Proof.
Let this straight line be \(BC\).

Use proposition 1 to construct an equilateral triangle \(ABC\) using \(BC\) as a base.
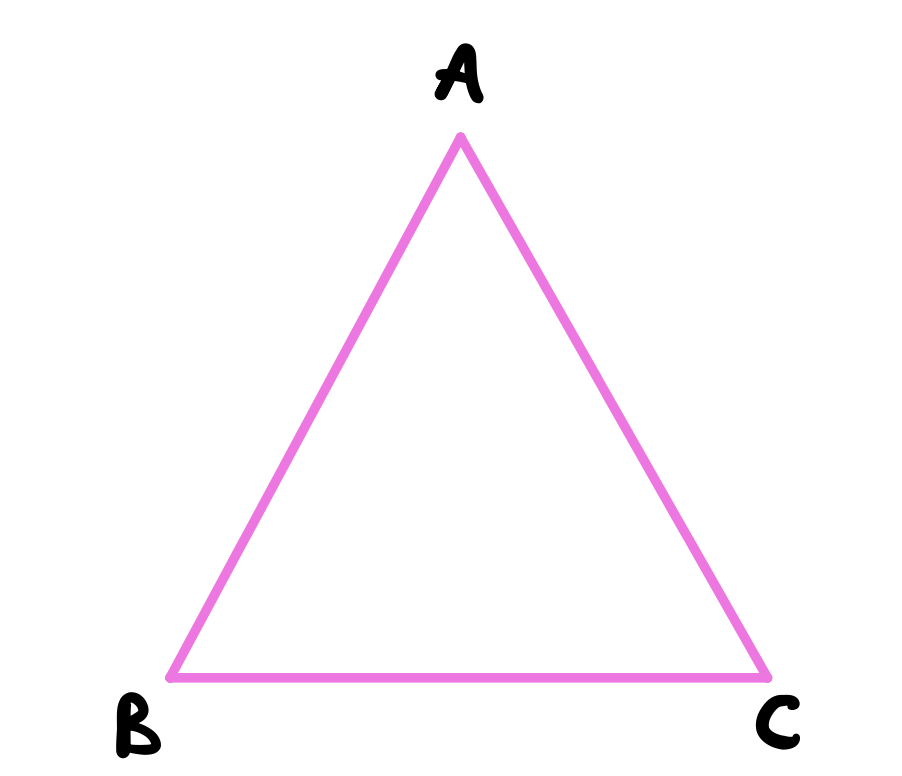
Bisect the angle \(A\) using proposition 9.
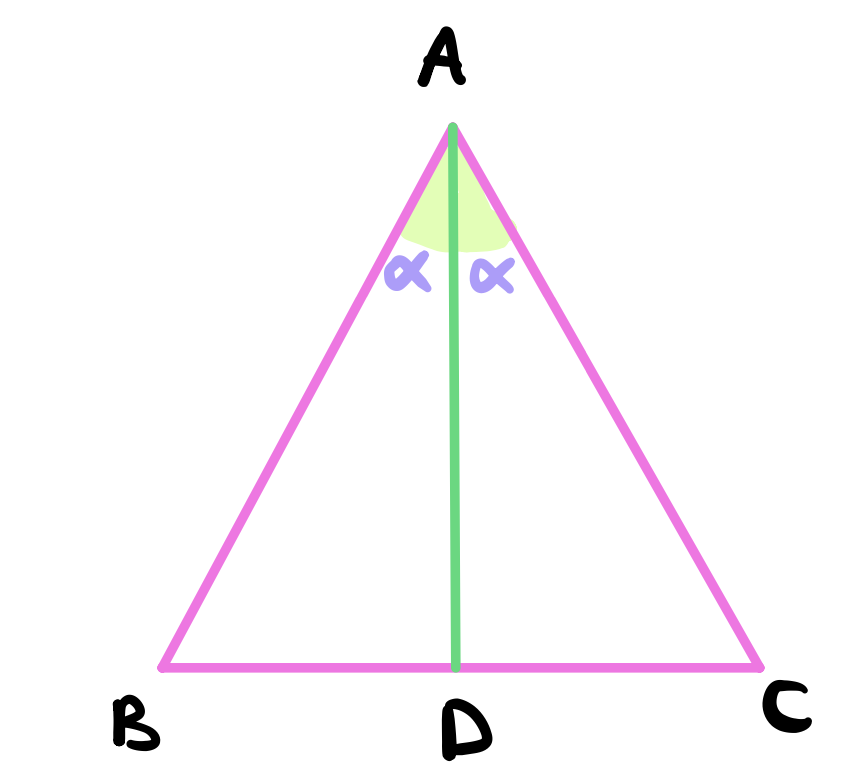
We claim that \(BD = DC\). To see this, notice in the triangles \(ABD\) and \(ADC\) below that \(AB = AC\) by construction, \(AD\) is common to both triangles, and \(\angle ABC = \angle ACD\) by construction.
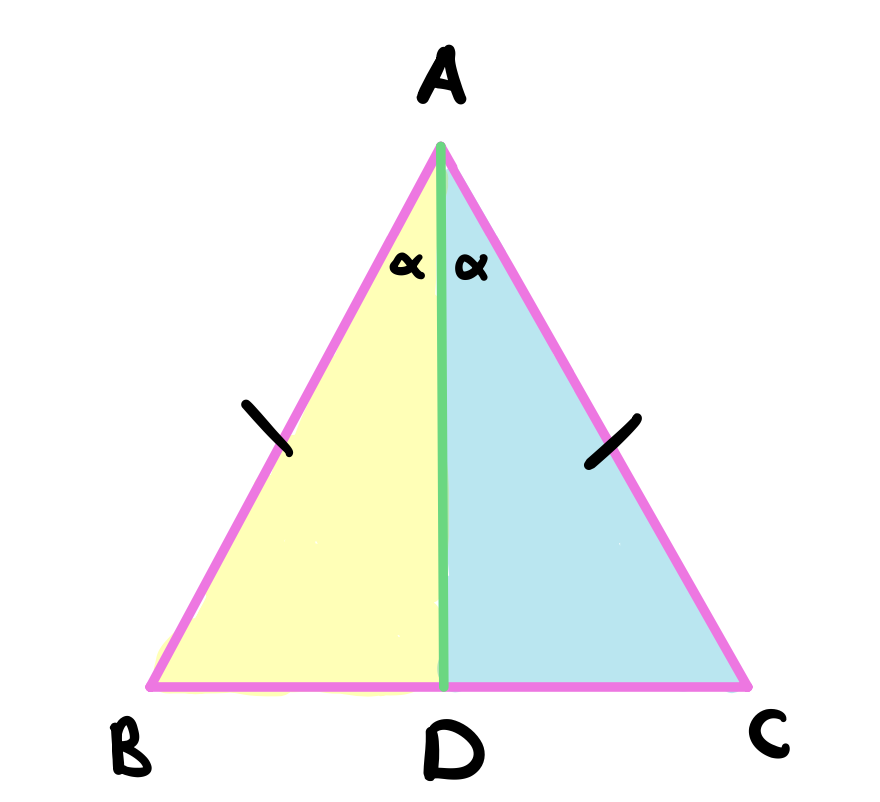
Therefore, we can conclude by proposition 4 that the triangles are equal in all respects and consequently we will have \(BD = DC\) as required.
Thoughts: pretty straight forward proof!
References: