Note: I was using Oliver Byrne’s book when I studied this proof. Axiom 10 doesn’t seem to exist in the original book
Proposition 4: Proposition 4: “IF two triangles have two sides of the one respectively equal to two sides of the other, and the angles contained by those equal sides also equal; then their bases or their sides are also equal: and the remaining and their remaining angles opposite to equal sides are respectively equal: and the triangles are equal in every respect.”
Basically, given two triangles where two of the sides are equal and the angles contained between the two sides in each triangle are also equal, then the two triangles are equal in every other respect meaning that the third side is also equal and the remaining two angles are equal as well.
Proof.
Let the triangles be \(ABC\) and \(DEF\). Let the two sides be arbitrarily chosen. Suppose we have \(AB = DE\) and \(BC = EF\) and the angle \(ABC = DEF\) (hypothesis).
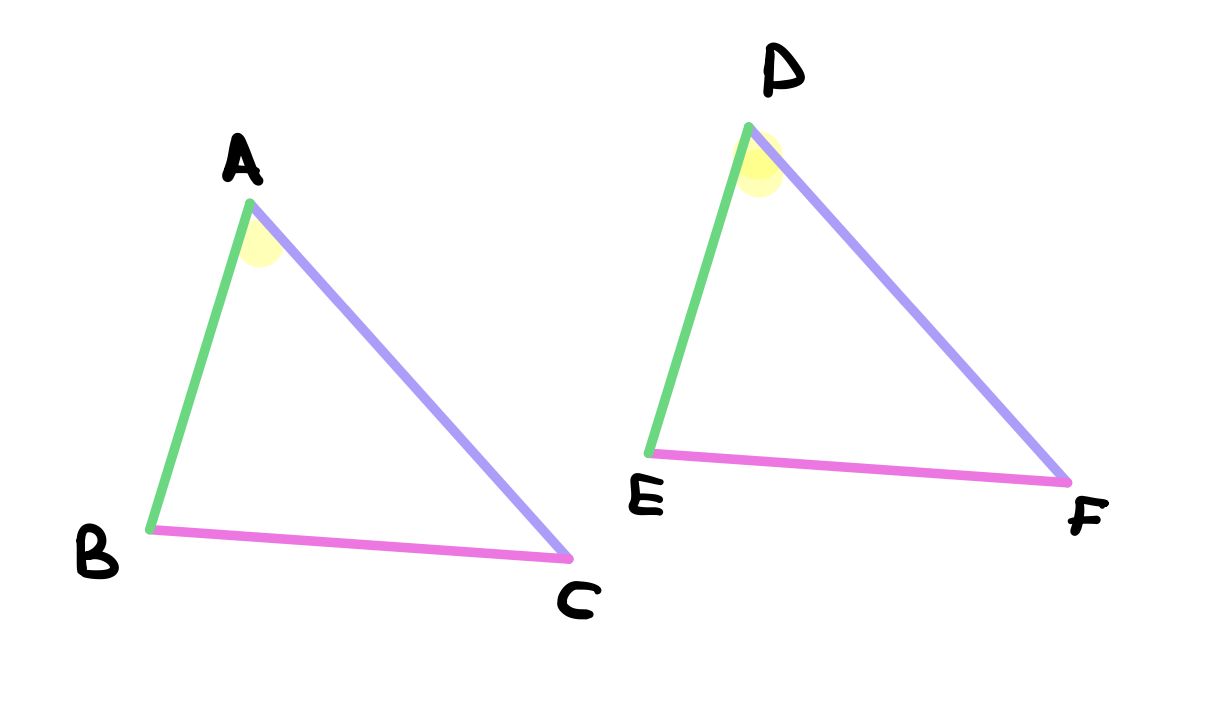
Now, place the vertex \(A\) onto the vertex \(D\). First, because the angles are equal, the line \(AB\) will fall onto the line \(DE\) (same direction) and second, because we know that \(AB = DE\), then the vertex \(B\) must coincide with the vertex \(E\). Similarly, the vertex \(C\) must coincide with the vertex \(F\).
Since the vertices \(B\) and \(E\) coincide with each other and the vertices \(C\) and \(F\) coincide with each other, then the side \(BC = EF\). If that’s not the case, then the straight lines connecting \(E\) and \(F\) and \(B\) and \(C\) will include a space but axiom 10 states that two straight lines cannot include a space. In other words, there is only one straight line between two points and therefore \(BC = EF\).
So now that we have all vertices coinciding with each other and all three sides coinciding with each other we can conclude that the two triangles coincide with each other and so they are equal in all respects due to axiom 8 (magnitudes which coincide with one another or exactly fill the same space, are equal).
Thoughts:
(1) When we placed \(A\) onto \(D\), we concluded two things. First, because the angles are equal, the line \(AB\) will fall onto the line \(DE\). Second, because it’s given than \(AB = DE\), then \(A\) must coincide with \(D\). I hard to wrap my head around this for a little longer.
(2) Instead of proving that the third side must be equal to the same third side of the second triangle, I think we could just conclude that the triangles are equal just from having the three vertices coinciding. This is because between any two points, we can only have one straight line (axiom 10) and so the two triangles must coincide and be equal to each other without having to prove the third side separately. (I think?)
Overall, this was a confusing proposition. What does placing a vertex on top another vertex even mean? I guess perhaps we could use proposition 2 to re-create the second triangle on top of the first triangle?
References: