Proposition 9: To bisect a given rectilineal angle.
Proof.
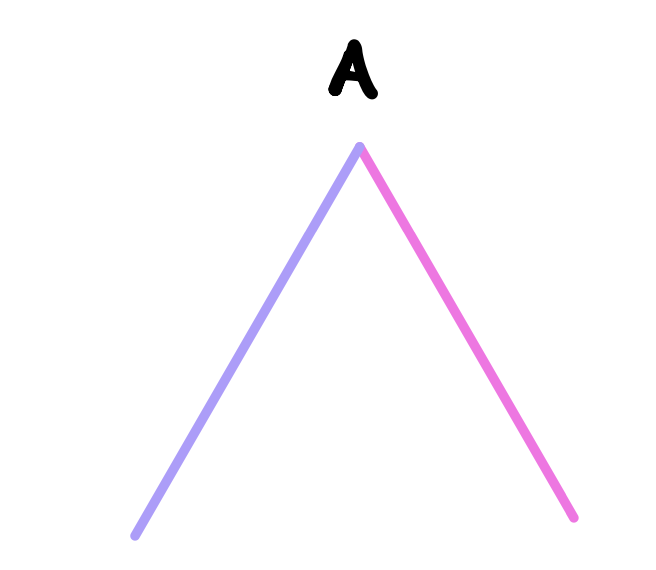
Given an angle \(A\) (a point \(A\) with two drawn lines that start at \(A\)). Choose a point on one of the extended lines arbitrarily. Let that point be \(B\).
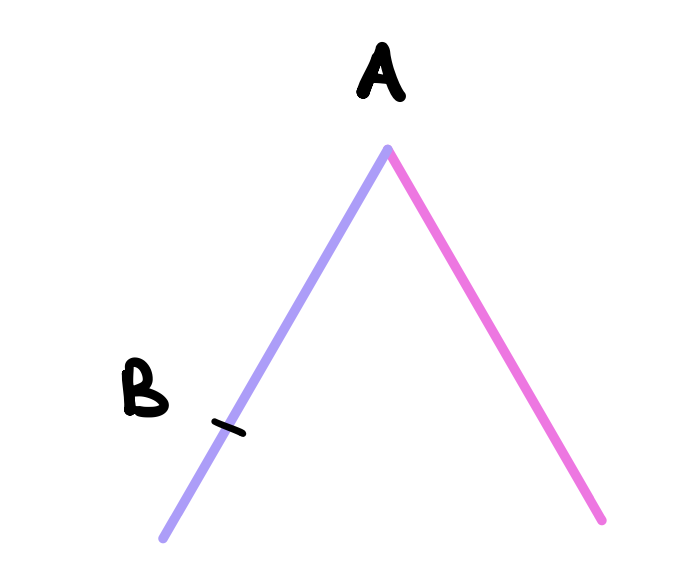
Use proposition 3 to cut a line equal to \(AB\) from the second line. Let that point be \(C\).
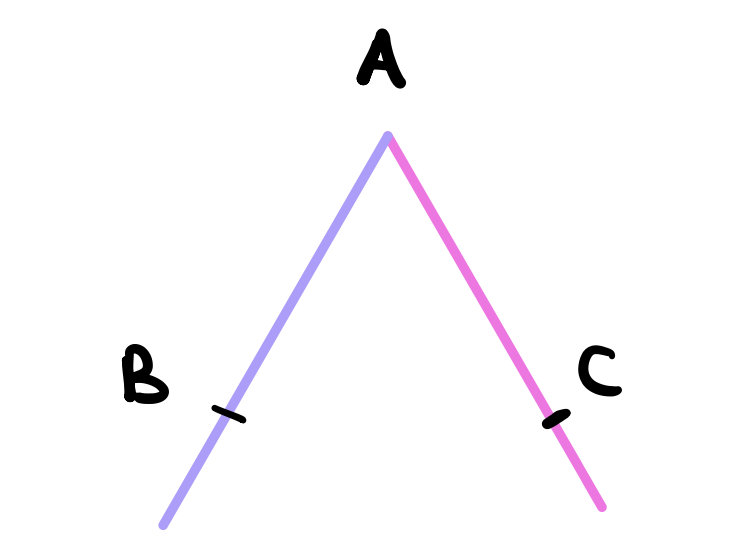
Use postulate 1 to draw a line between the two points \(B\) and \(C\).
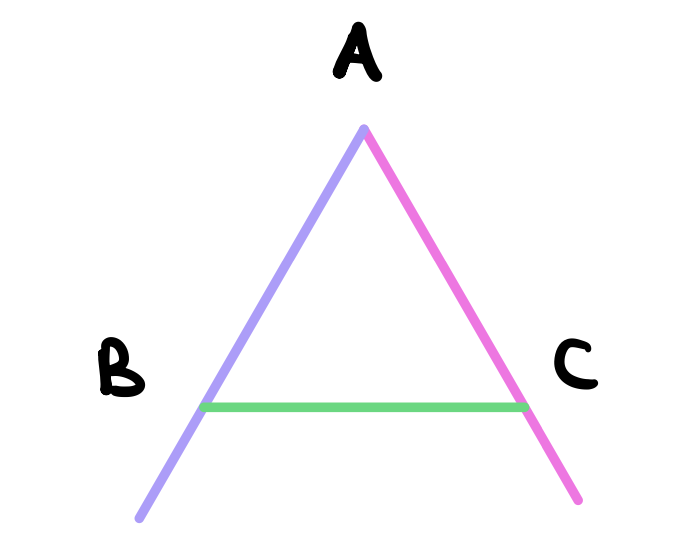
Next, use proposition 1 to construct an equilateral triangle from the line \(BC\).
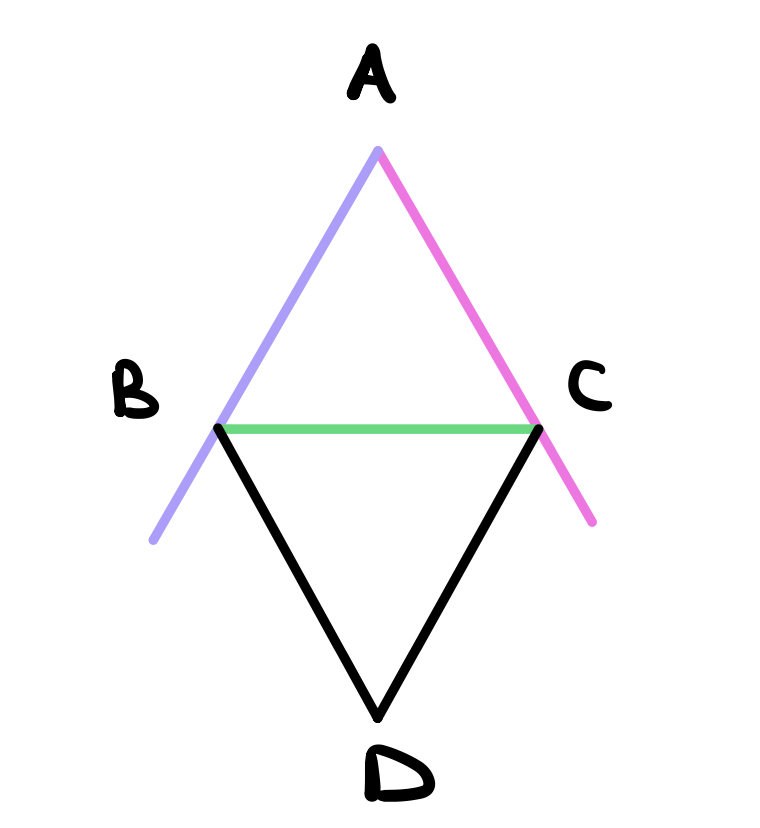
Use postulate 1 to draw a line between the two points \(A\) and \(D\). We claim that this line bisects the angle \(A\).
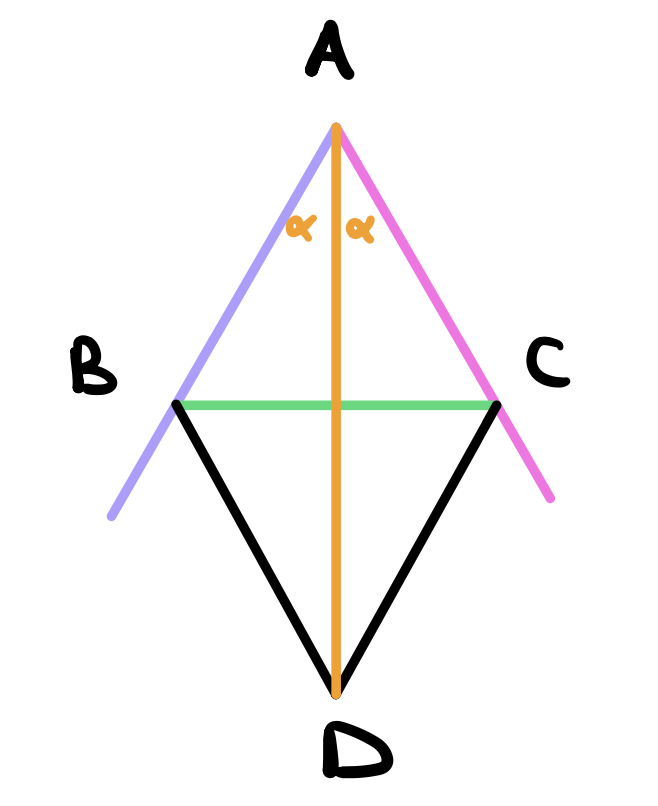
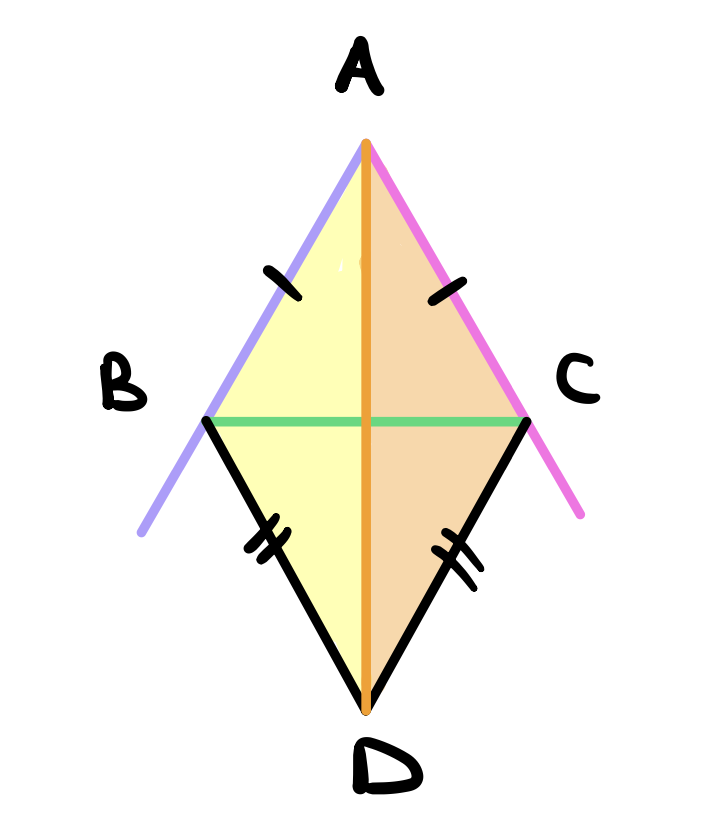
To see this, notice that in the triangles \(ABD\) and \(ACD\), \(AB = AC\) and \(BD = CD\) by construction. Moreover, \(AD\) is a common side to both triangles. Therefore, by proposition 8, we conclude that the angles \(\angle BAD\) and \(\angle DAC\) are equal. as required.
Thoughts: -
References: