Proposition 6: “If in a triangle two angles be equal to one another, the sides which subtend the equal angles will also be equal to one another.”

Proof.

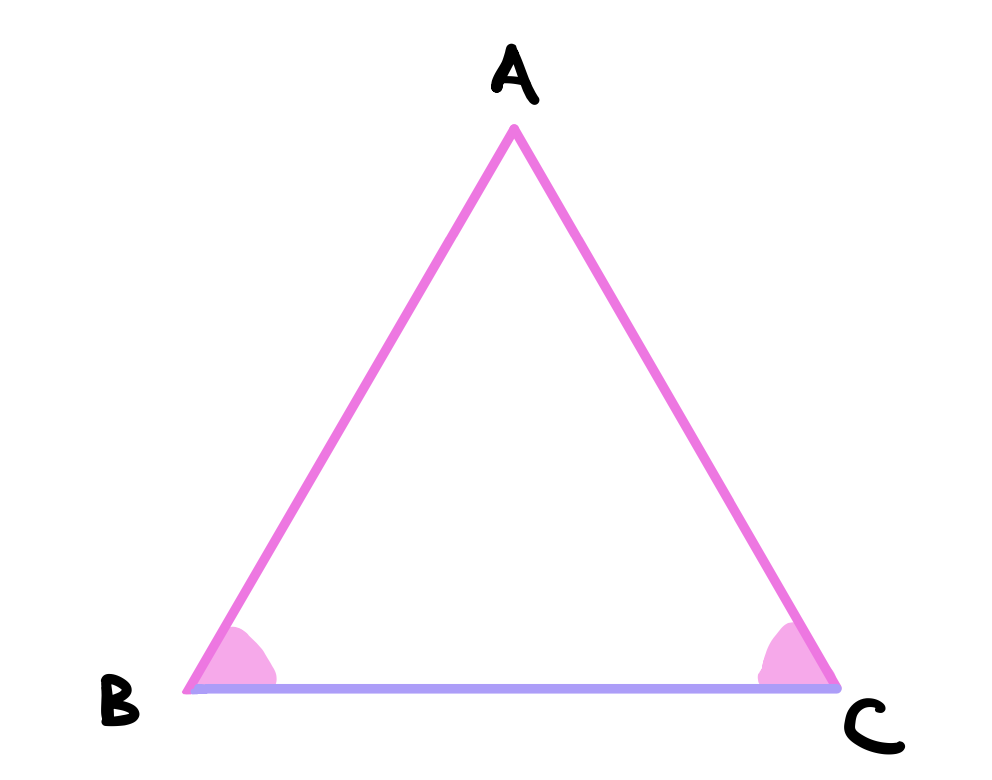
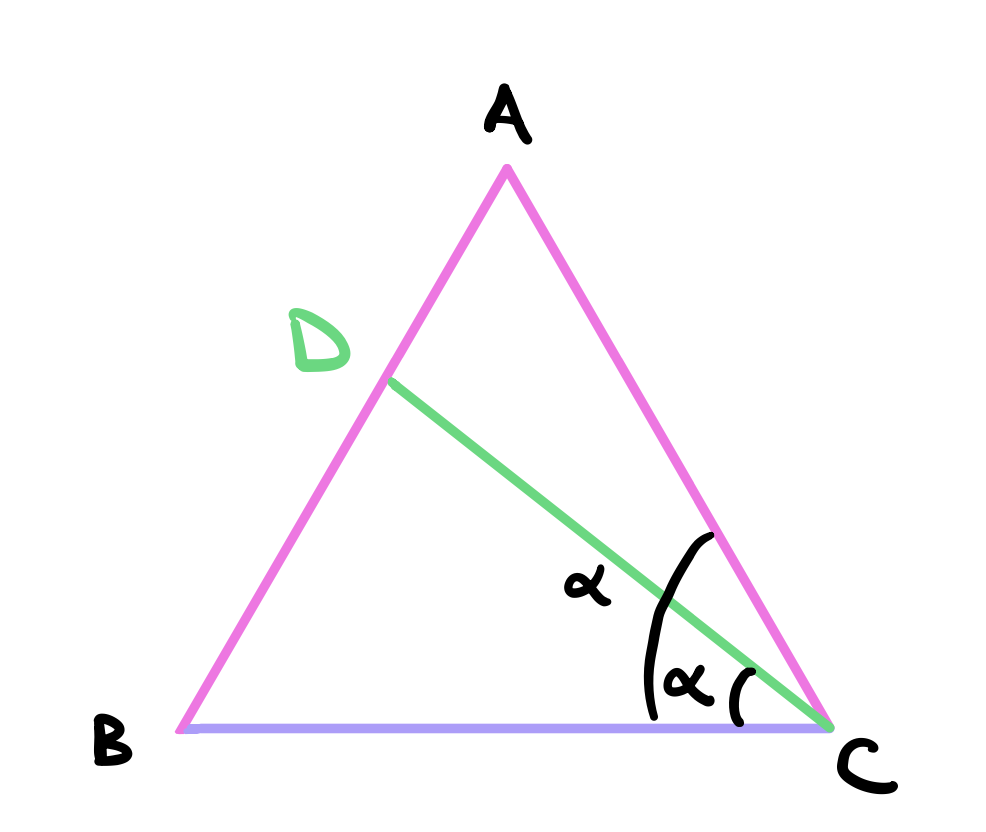
Let the triangle be \(ABC\). Choose two angles to be equal. Suppose we let \(\angle B = \angle C\). We will prove that \(AB = AC\). Suppose they are not. This means that one of them is greater than the other. Choose one arbitrarily to be the greater one. Suppose it is \(AB\). Use proposition 3 to cut a line from \(AB\) equal to \(AC\). Let the cut line be \(DB\).

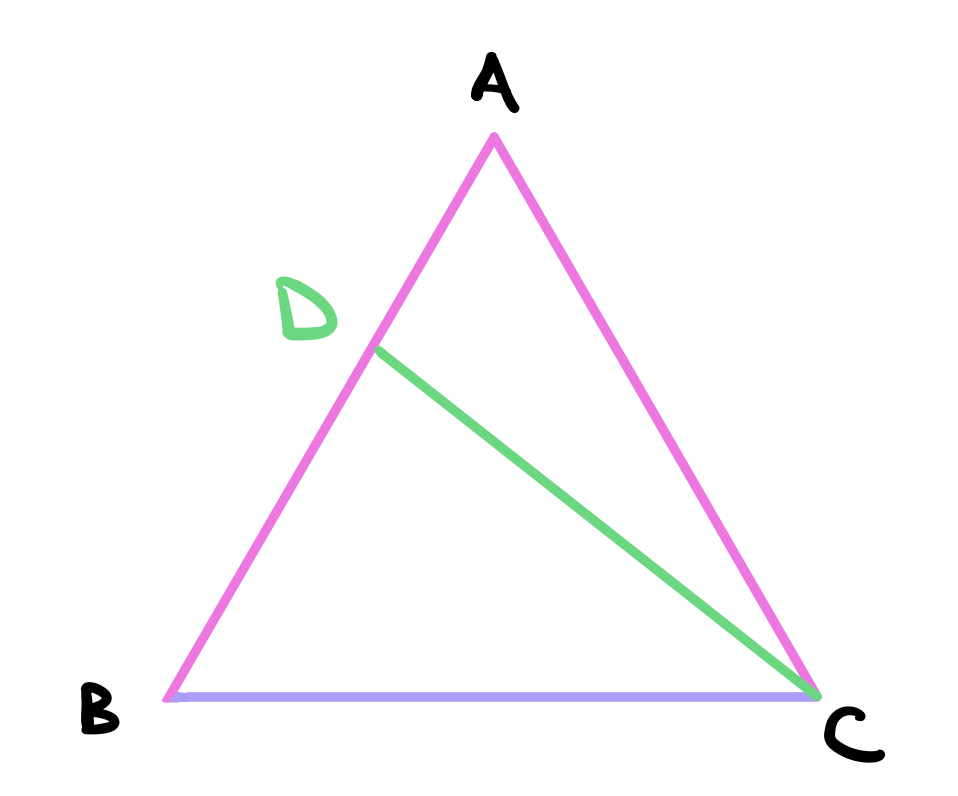
In the triangles \(ABC\) and \(DBC\), first \(DB = AC\) by construction. Second, \(BC\) is a common base. Third, \(\angle DBC\) is a common angle. From this we can conclude that the triangles are equal in all respects by proposition 4

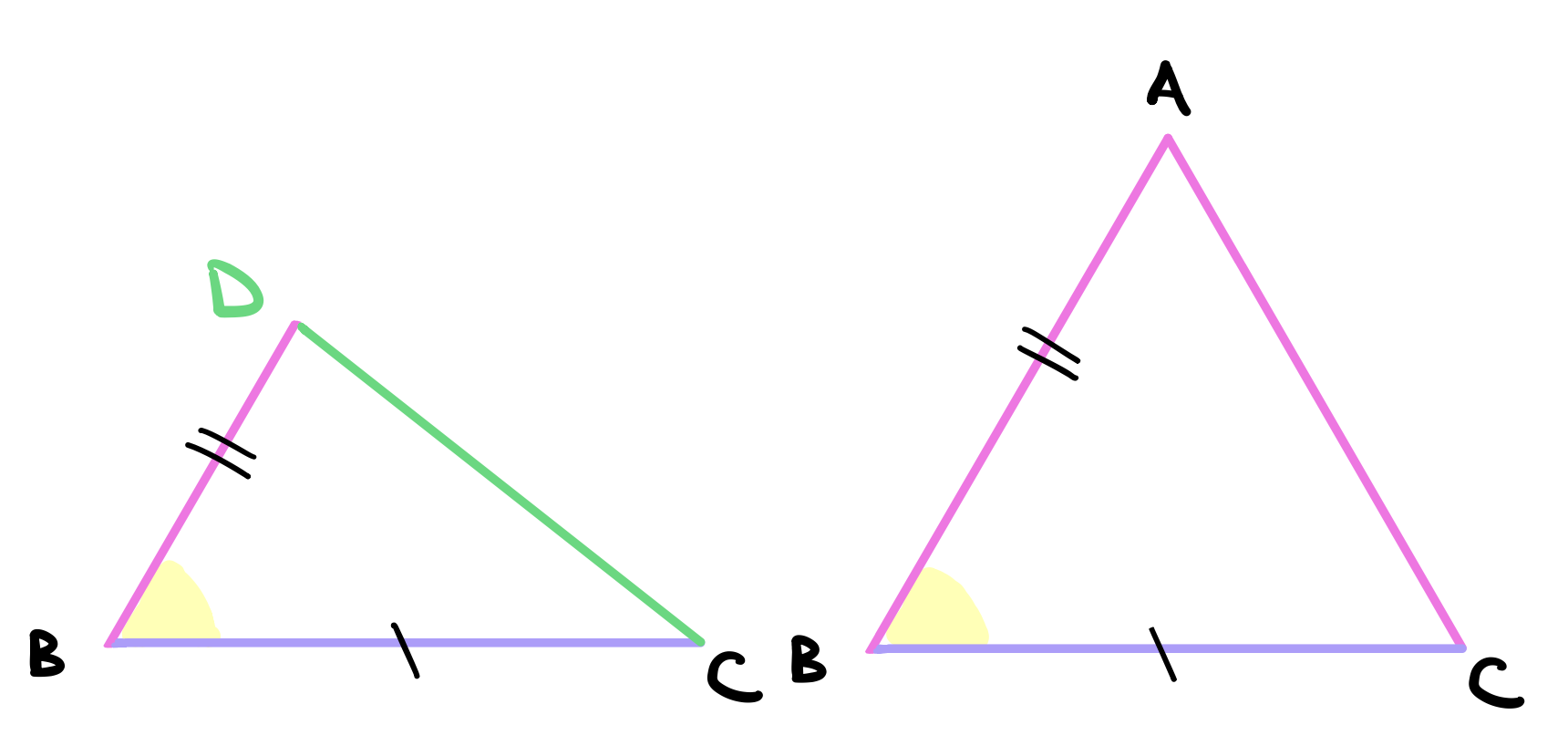
Consequently, w\(\angle ACB = \angle DCB\) let this angle be \(\alpha\).

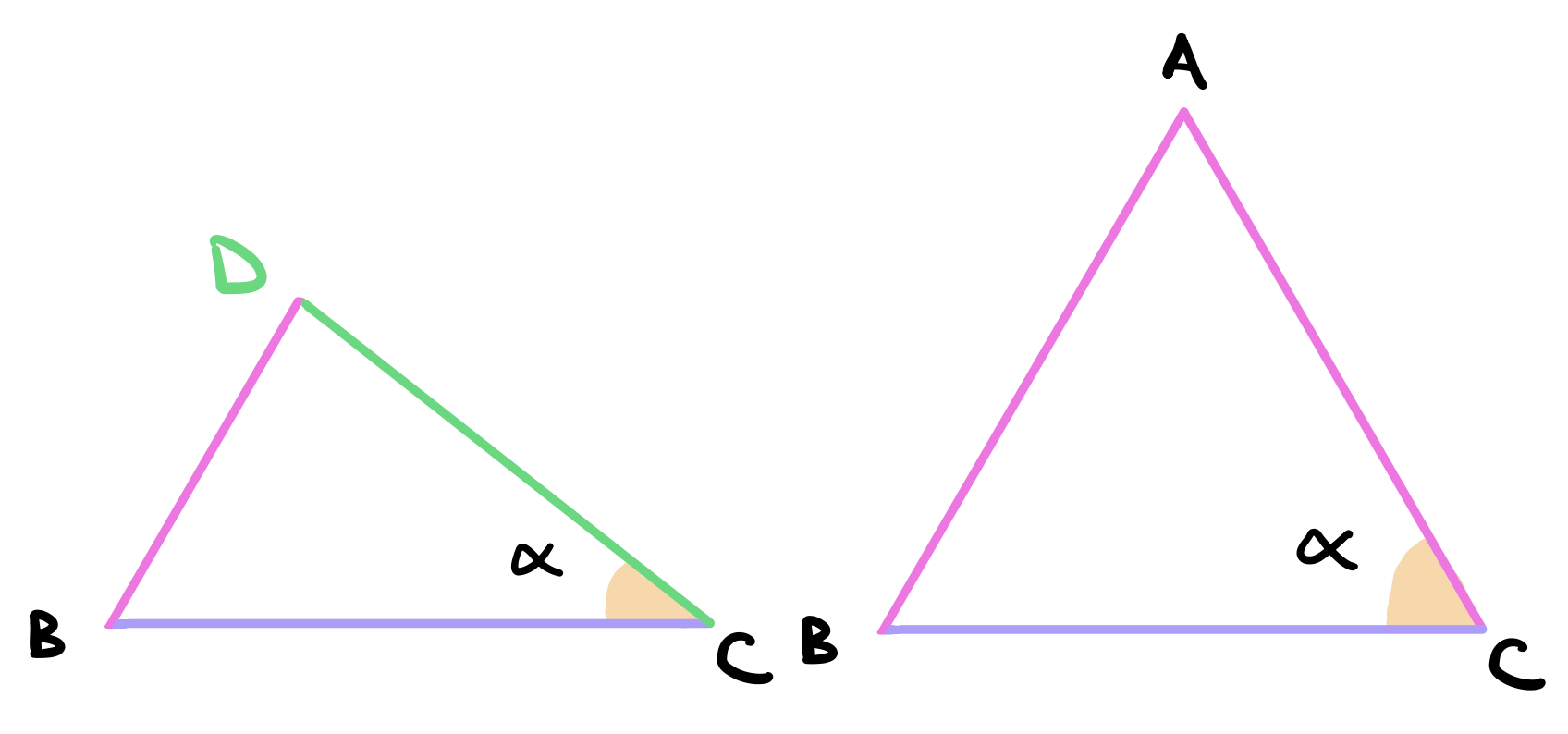
But angle \(\angle ACB\) equals to the sum of angles \(\angle ACD\) and \(\angle DCB\). Since \(\angle ACB = \angle DCB = \alpha\), this implies that \(\angle ACD\) must be 0, but this is impossible because this means that the vertices \(A\) and \(D\) are the same and we assumed that \(AB\) is greater. So \(AB\) must be equal to \(AC\).

Thoughts: -

References: