Proposition 5: “In isosceles triangles the angles at the base are equal to one another, and, if the equal straight lines be produced further, the angles under the base will be equal to one another.”
Construction.
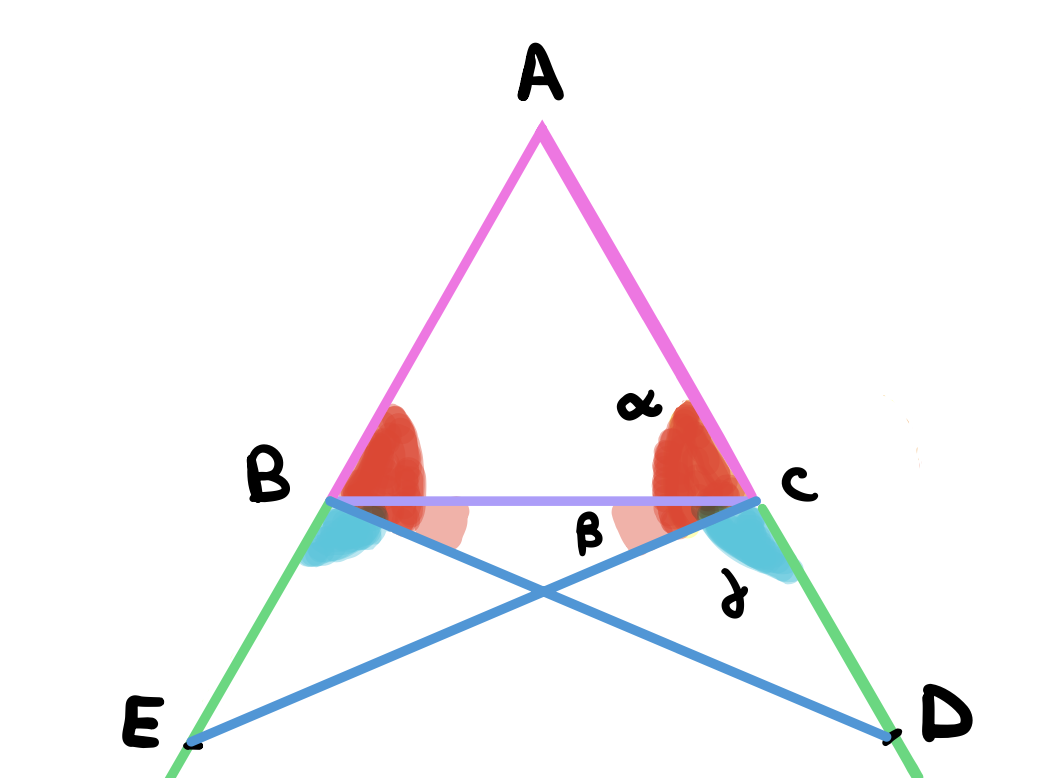
Let \(ABC\) be a triangle with two equal sides. Let the equal sides be \(AB\) and \(AC\). This triangle can be easily constructed by drawing a point and then describing a circle with the center at the given point and a radius of a given length using postulate 3. We can then draw two lines from the center to the edge of the circle. These lines are equal by definition 15. Furthermore we can draw a third line connecting the two intersection points to form an isosceles triangle using postulate 1.
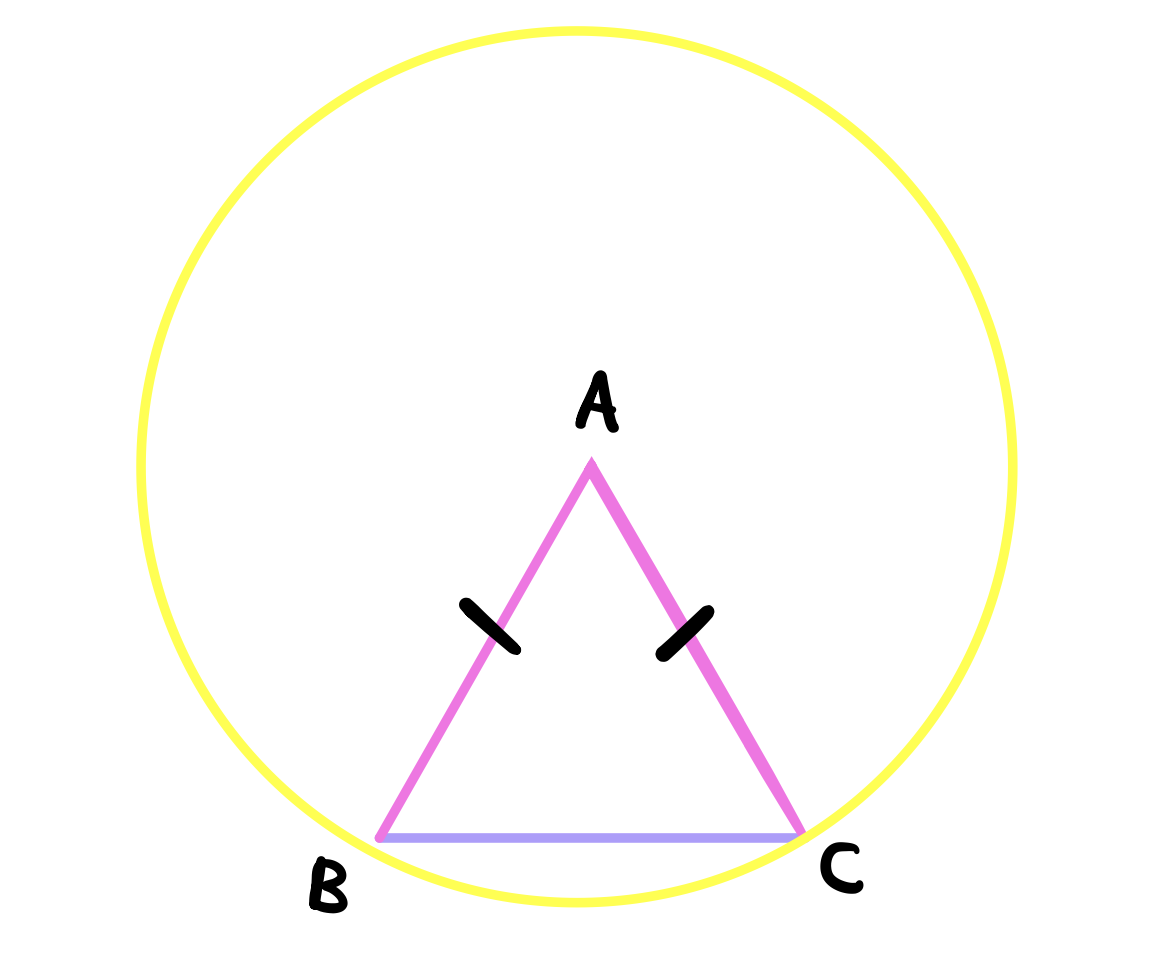
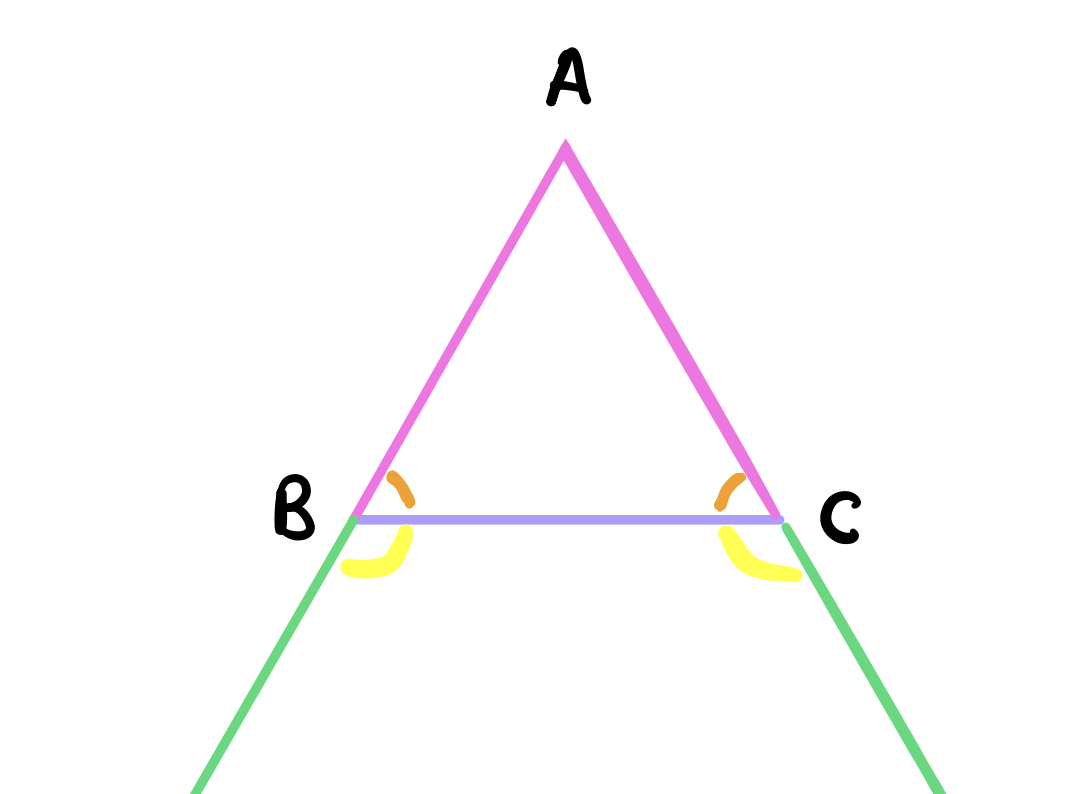
Using postulate 2, we can extend the lines \(AB\) and \(AC\) further down. The claim is that the orange and yellow angles below must be equal.
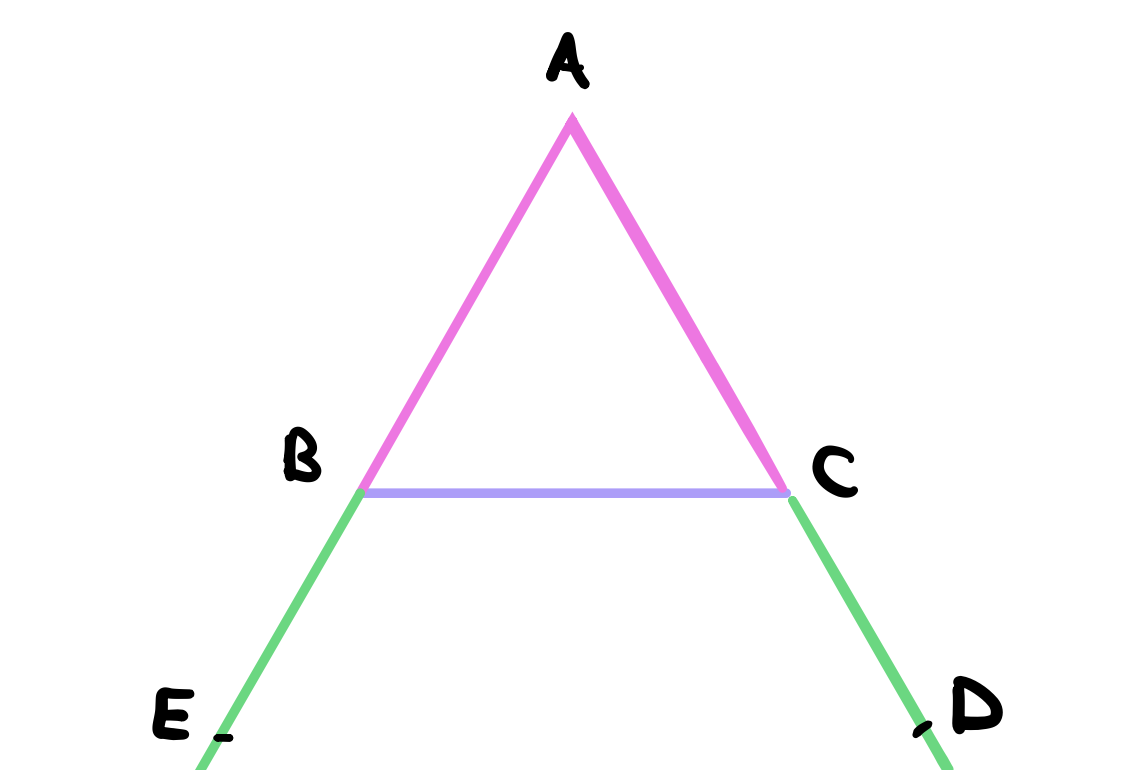
Define some point arbitrarily chosen along the extended line that we drew from point \(B\). Let this point be \(E\). Using proposition 2, we can define point \(D\) on the other side such that \(BE = CD\).
Using postulate 1, connect the lines between the points \(C\) and \(E\) and then again between the points \(B\) and \(D\).
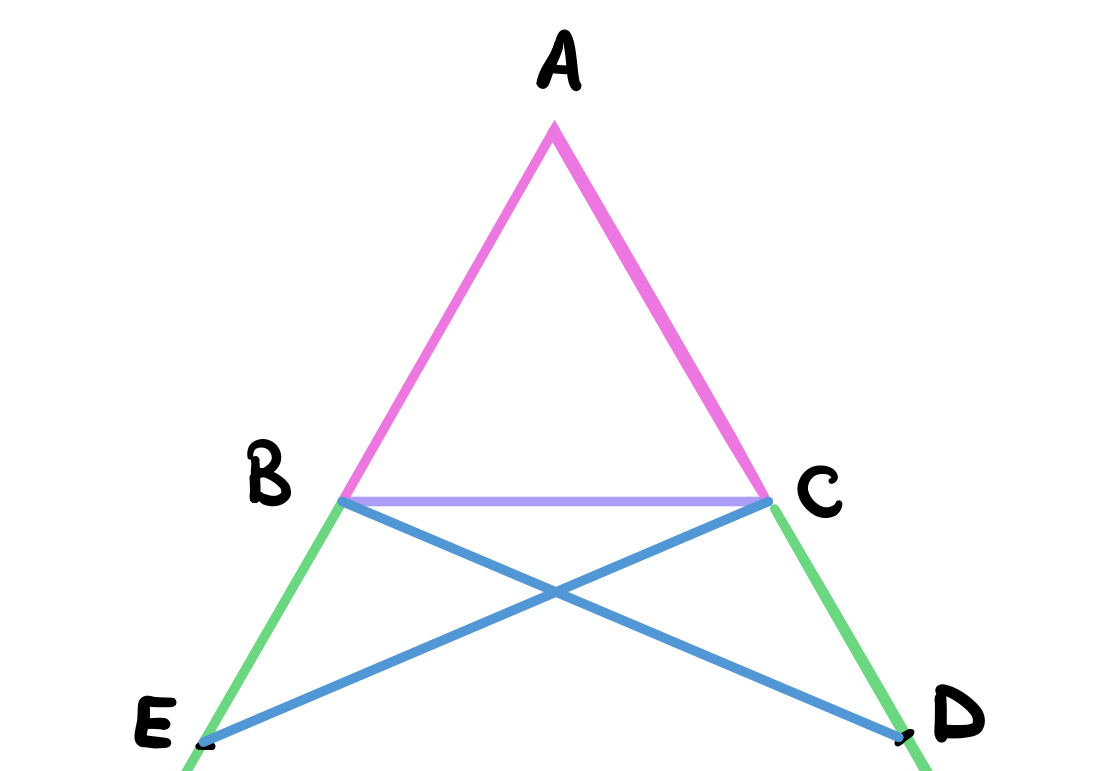
Proof.
In the shaded triangles \(AEC\) and \(ADB\), first, the triangles share an angle \(A\). Second, \(AC = AB\) by construction. Third, \(AE = AD\). This is because \(AB = AC\) and \(BE = CD\) (both by construction). Therefore \(AB + BE = AC + CD\) and so \(AE = AD\) by common notion 2 (if equals are added to equal parts, then the wholes are equal). Since we have one angle and the two sides connecting it all equal then we can conclude that by proposition 4, the triangles are equal.
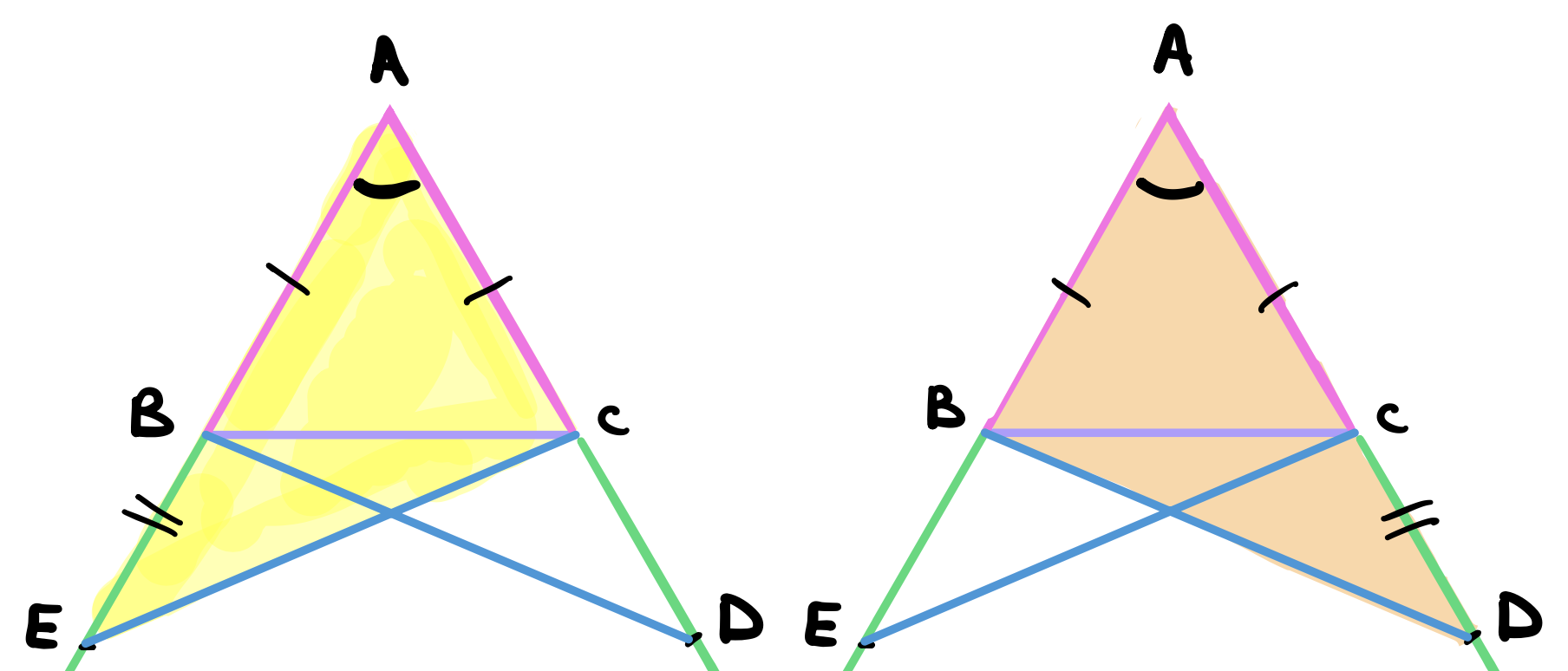
Consequently, the highlighted angles below are equal. Namely \(\angle ACE = \angle ABD = \alpha\) and \(\angle AEC = \angle ADB\). Furthermore, the blue lines are also equal, namely \(BD = CE\).
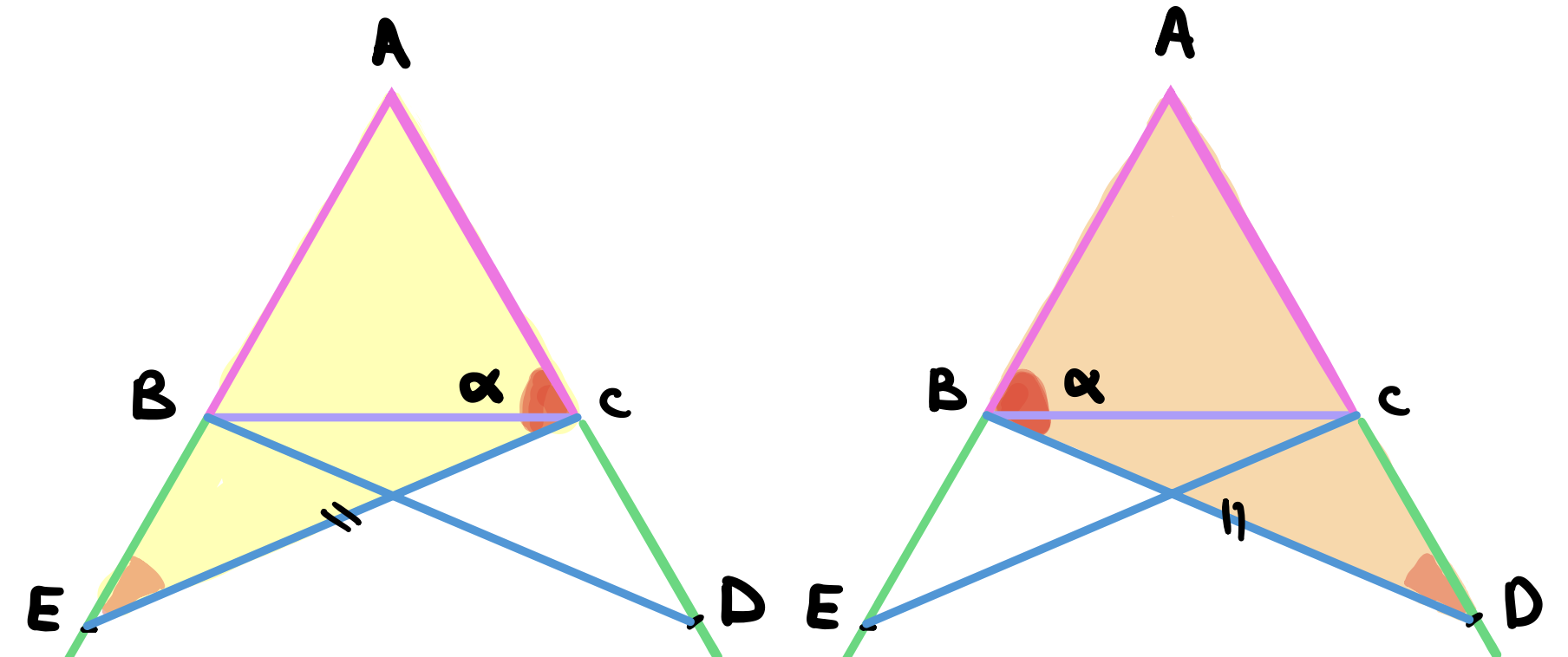
Next, consider the triangles \(BEC\) and \(BCD\) below. We claim that the triangles are also equal. To see this, we know that angles \(\angle AEC = \angle ADB\) are equal (previously proven above). We also know that the sides \(BD\) and \(CE\) are also equal. lastly, \(CD =\)BE$$ by construction. Therefore, these triangles are also equal in all respects by proposition 4.
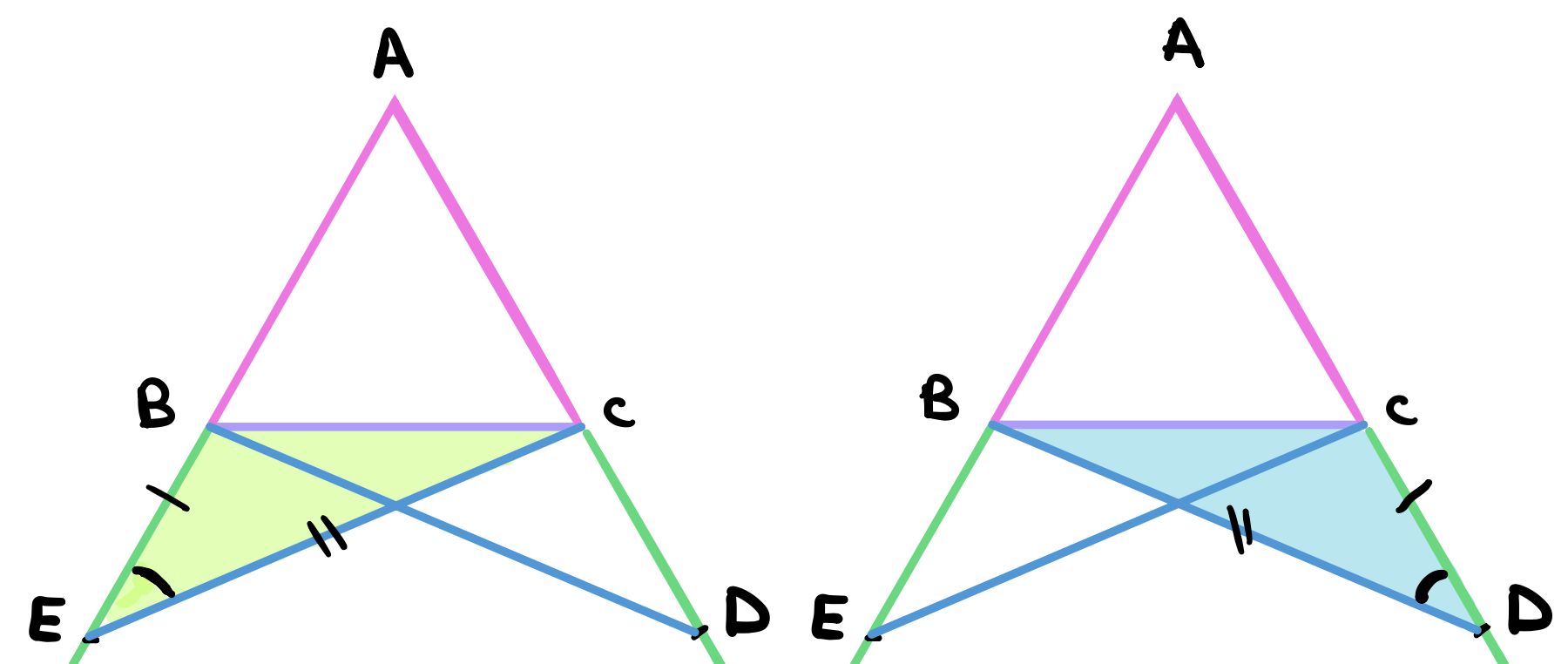
Consequently, the highlighted angles will be equal, \(\angle BCE = \angle CBD = \beta\) and \(\angle EBC = \angle BCD = \gamma\).
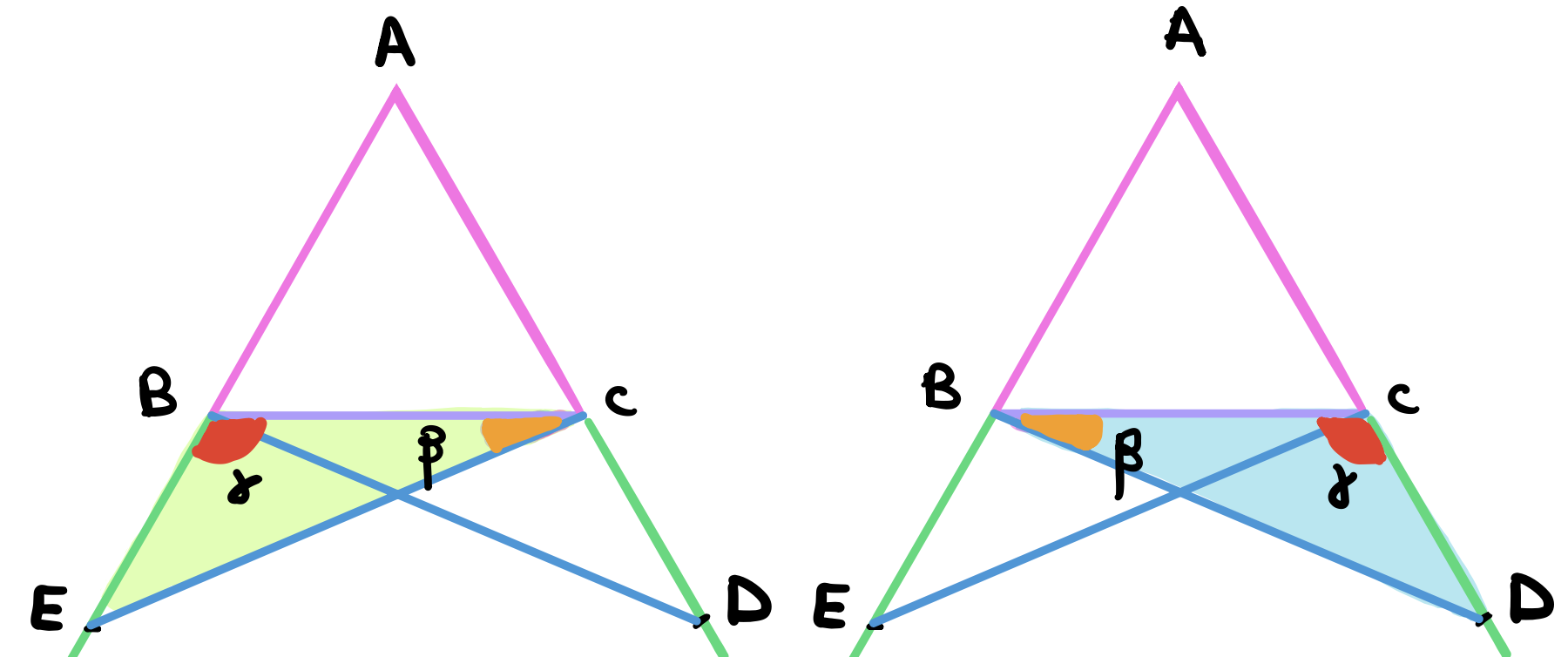
So far we’ve proven \(\angle ACE = \angle ABD = \alpha\) and \(\angle BCE = \angle CBD = \beta\). Therefore, the internal angles \(ACB\) and \(ABD\) are equal due to common notion 3 (If equals be taken away from equals the remainders will be equal). Furthermore, we also proved that \(\angle EBC = \angle BCD = \gamma\). Therefore the external angles are also equal by using common notion 2 (If equals be added to equals, the wholes are equal).
Thoughts: -
References: