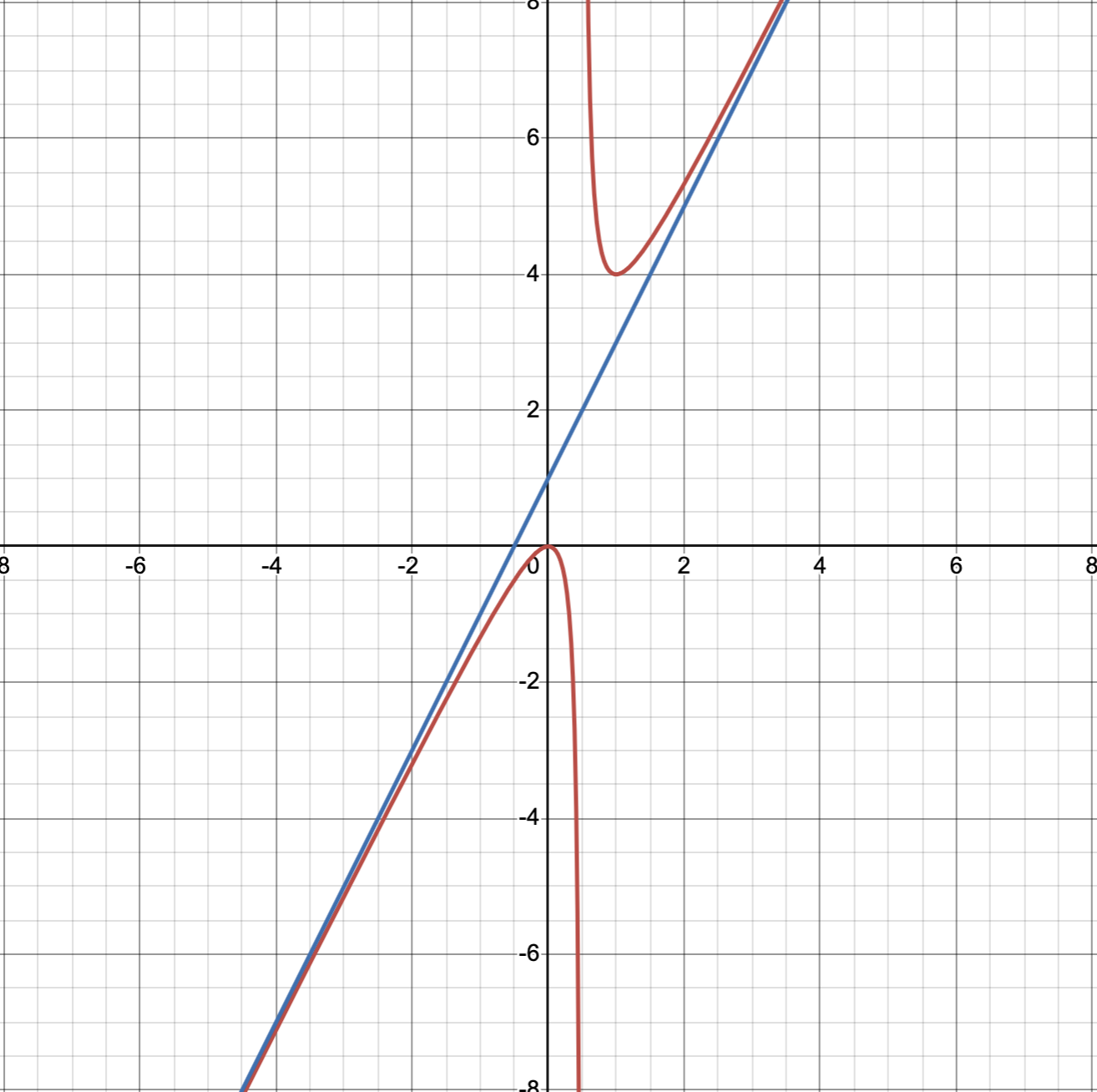
Given some function \(f\). A slanted asymptote occurs when the degree of the numerator (\(m\)) is larger than the degree of the denominator (\(n\)) by exactly 1 so \(m = n + 1\).

To re-iterate from the horizontal asymptotes post, we have three cases:

  • The case when \(m = n\). Here, we'll have a horizontal asymptote at \(a_m/a_n\) where \(a_m\) and \(a_n\) are the leading coefficients of each of the highest terms
  • The case when \(m < n\). Here, we'll have a horizontal asymptote at \(y = 0\).
  • The case when \(m > n\). Here we won't have a horizontal asymptote and for \(m = n + 1\) we will have a slanted asymptote which is what this post is about!


Finding the Slanted Asymptote

For example, suppose we have the function,

$$ \begin{align*} f(x) &= \frac{3x^4-x^2}{x^3-x^2+1} \end{align*} $$

We said before that when we study the end behavior of rational functions, we will focus on the largest power in both the numerator and the denominator. This is because as the input gets larger and larger (end behavior!), only the largest powers will matter and will completely take over in determining how the functions will behave). So let’s focus on the these only,

$$ \begin{align*} f(x) &\approx \frac{3x^4}{x^3} \\ &\approx 3x \\ \end{align*} $$

When \(x\) approaches positive infinity, this function will also approach positive infinity. Similarly, as \(x\) approaches negative infinity, the function approach negative infinity. This line \(y=3x\) has a slope of 3 which the slanted asymptote will follow.

However find the slope isn’t enough because we need to find the equation of the whole line/asymptote. So we still need to find the \(y\) intercept which will require us to perform long division to find it.

Finding the \(y\) Intercept of the Slanted Asymptote

We’ll divide the numerator by the denominator (see video for how it’s done). The divison will result in \(3x + 3\) and some remainder. We won’t care about the remainder since as we approach infinity, the remainder will approach zero. So the equation of the slanted asymptote will just be \(3x + 3\) and this is exactly the slanted asymptote we’re looking for.



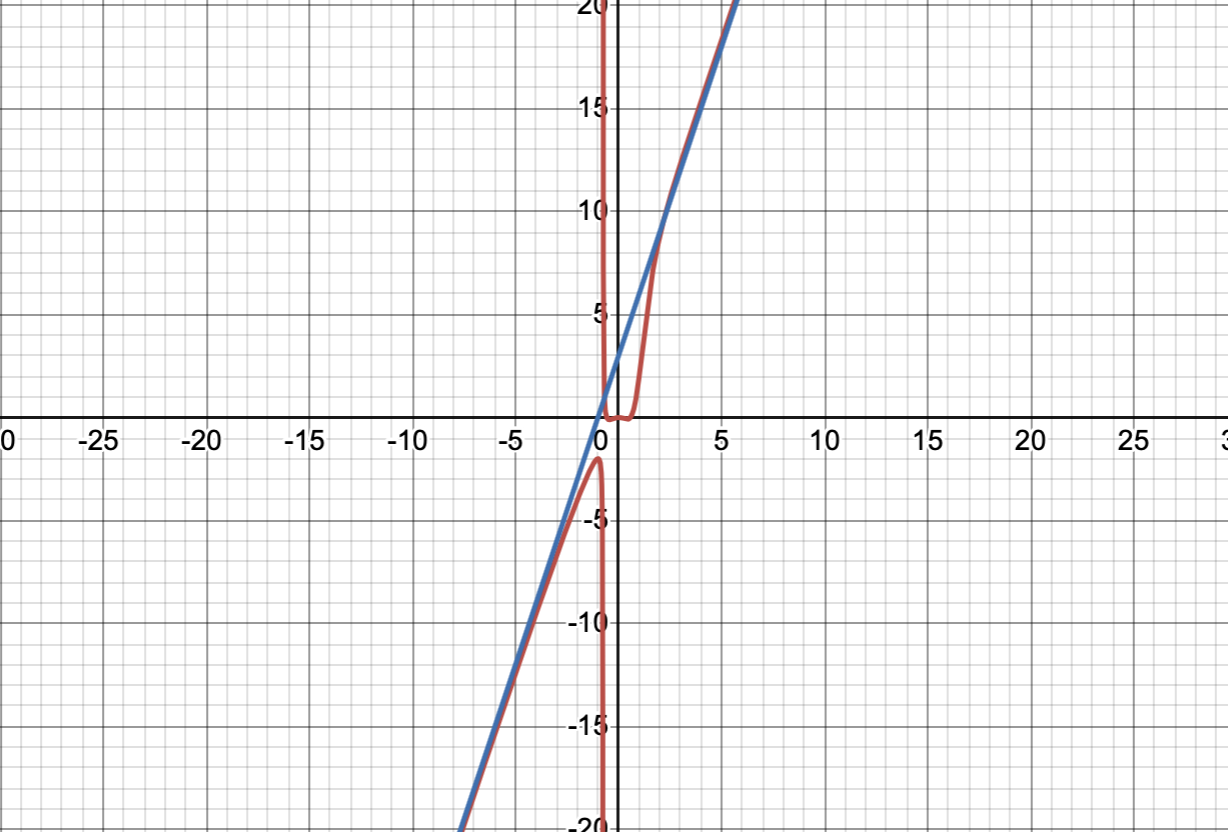
Can you cross a slanted asymptote

yes. we can definitely cross a slanted asymptote especially when it’s still early. The horizontal and slanted asymptotes show their effects more as \(x\) gets really large (whether toward positive or negative infinity).

References: