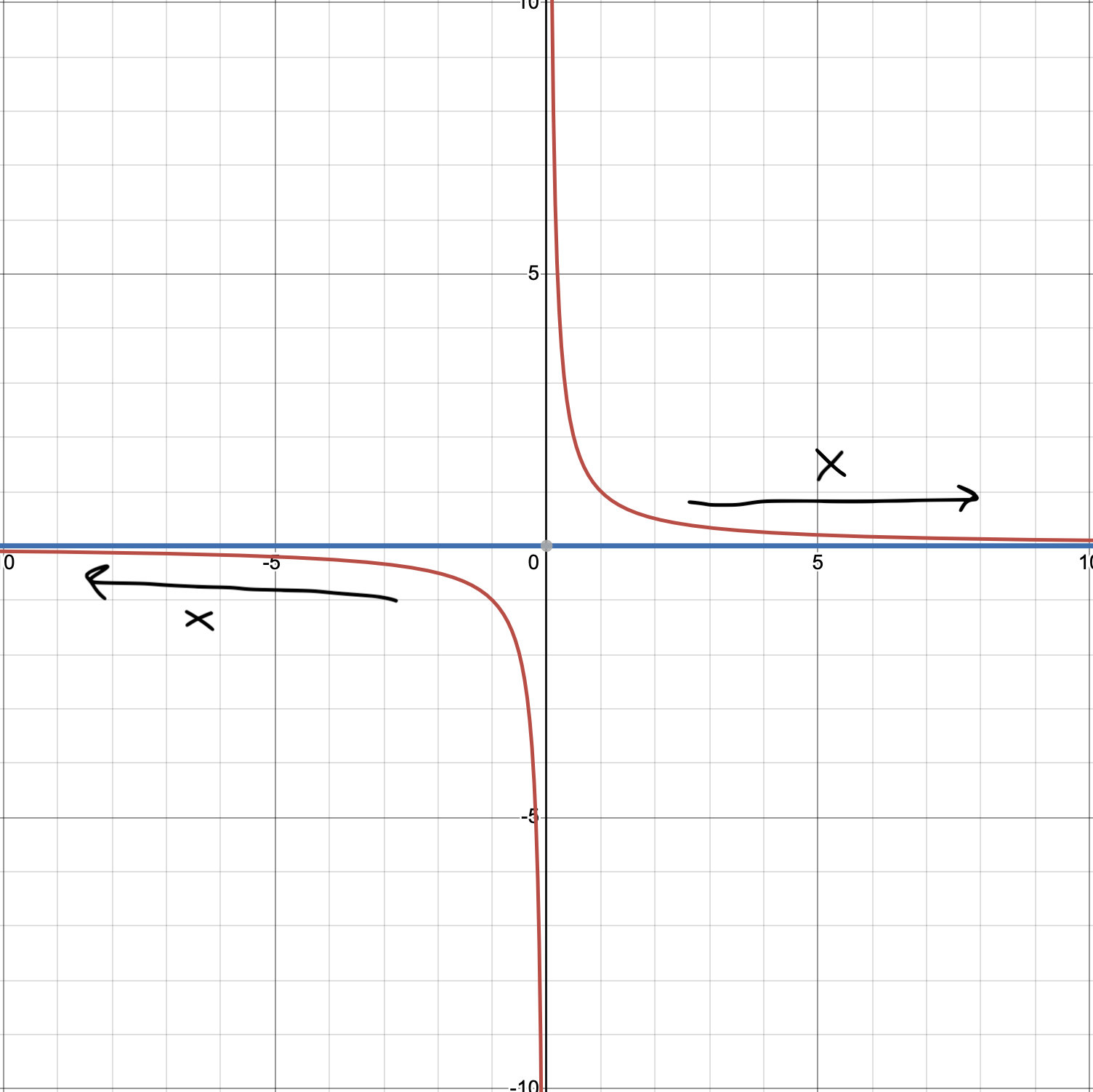
Given some function $f$. A horizontal asymptote is a line $y=a$ where as the input $x$ to the function approaches negative or positive infinity, we will find that $f(x)$ will approach $b$. (So just the opposite of vertical asymptotes where as $x$ approaches $a$, we will approach positive or negative infinity. For example, for $f(x)=\frac{1}{x}$, as we plug in very large values of $x$ (whether positive or negative), we will notice that $f(x)$ will get closer to zero! So the line $y=0$ is a horizontal asymptote for the graph of the function $f(x)=\frac{1}{x}$.

Finding a Horizontal Asymptote

The end behavior of a rational function is determined by the leading terms in the numerator and the denominator. Intuitively this makes total sense because as we plug in really large values of $x$, the leading term will be the only thing matters. Because of this, we want to focus on only these leading terms. For example if we have,

$$ \begin{align*} f(x) &= \frac{a_mx^m+a_{m-1}x^{m-1}+...}{a_nx^n+a_{n-1}x^{n-1}+...} \end{align*} $$

Then we’ll want to study,

$$ \begin{align*} f(x) \approx \frac{a_mx}{a_nx} \end{align*} $$

The degree of the numerator is $m$ and the degree of the denominator is $n$. Horizontal asymptotes occur only when $m \leq n$.

Case 1: $$m < n$$

What happens to the rational when the degree of the numerator is less than the degree of denominator. Take the example of $1/x$ again. We have degree 0 in the numerator and degree 1 in the denominator. You can see here as that as you plug in larger and larger values of $x$, the function will approach zero. Similarly take the function,

$$ \begin{align*} g(x) = \frac{x^2 + x + 3}{x^5 + 5x^4 + x^3 + 3x^2 + 5x - 21} \end{align*} $$

The degree of the numerator is 2 while the degree of the denominator is 5. Let’s focus on each leading term

$$ \begin{align*} g(x) &\approx \frac{x^2}{x^5} \\ &\approx \frac{1}{x^3} \end{align*} $$

We can see here that it simplified again to a constant up in the numerator. Again, as $x$ gets larger, we will approach zero. This is the reason why the rule simply states that if $m < n$, then the horizontal asymptote will always be at $y=0$.

Case 2: $$m = n$$

To study the behavior of a rational function when $m = n$, we will again focus on the leading terms in the numerator and the denominator. For example, if we have

$$ \begin{align*} g(x) = \frac{4x^3 + x^2 + x + 3}{2x^3 + 3x^2 + 5x - 21} \end{align*} $$

then we’ll focus on,

$$ \begin{align*} g(x) &\approx \frac{4x^3}{2x^3} \\ &\approx 2 \end{align*} $$

This simply states that as we plug in larger and larger values of $x$, we will notice that our function is approaching the line $y = 2$. Hence the rule states that the horizontal asymptote for when $m = n$, is the leading coefficient of the numerator divided by the leading coefficient of the denominator.

Can you cross a horizontal asymptote?

Yes! unlike vertical asymptotes, we can cross horizontal asymptotes.

References: