Proposition 13: If a straight line set up on a straight line make angles, it will make either two right angles or angles equal to two right angles.

Proof.

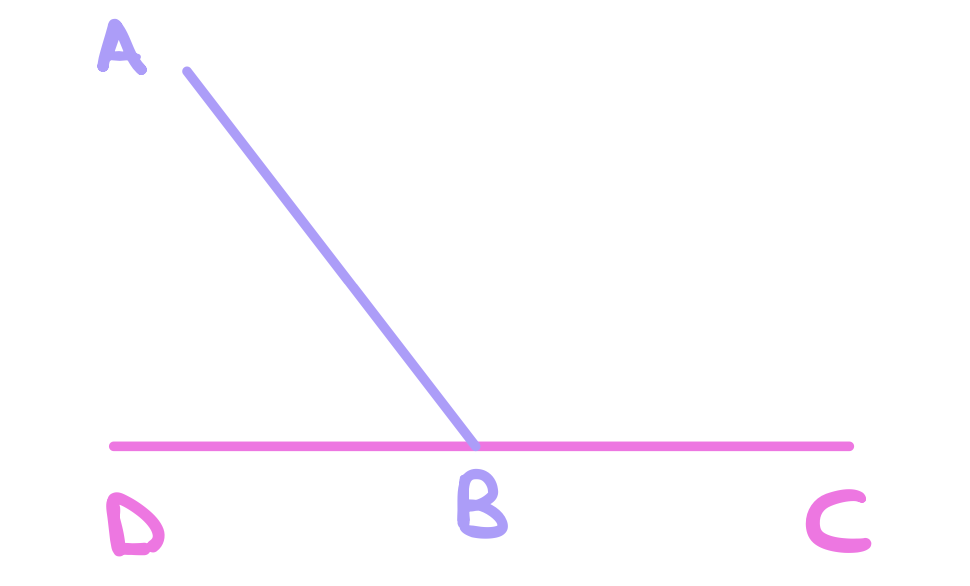
Suppose we have a straight line $AB$ set up on another straight line $CD$. We claim that the angles $\angle DBA$ and $ABC$ are either two right angles or equal to two right angles.

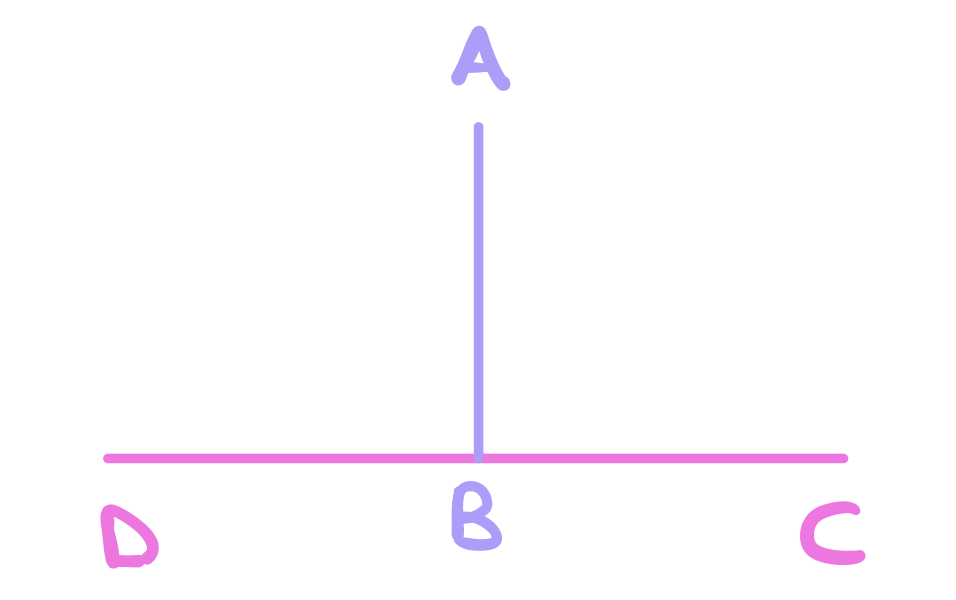
If both angles are equal to each other then by definition 10, they are both right angles and we are done. Otherwise, they are not. In this case, use proposition 11 to draw a perpendicular straight line from $B$ to $E$.

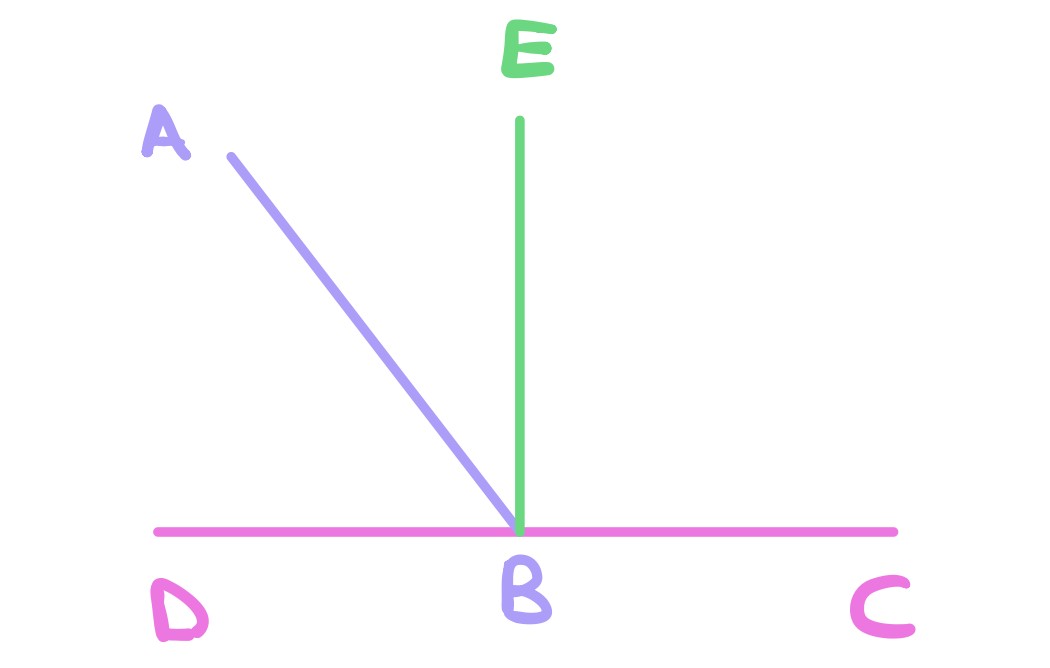
From proposition 12, we know that the angles $\angle DBE$ and $\angle EBC$ are both right angles. We also know that $\angle DBE$ is equal to the angles $\angle ABE$ and $\angle DBA$. Let the angle $\angle EBC$ be added to each,

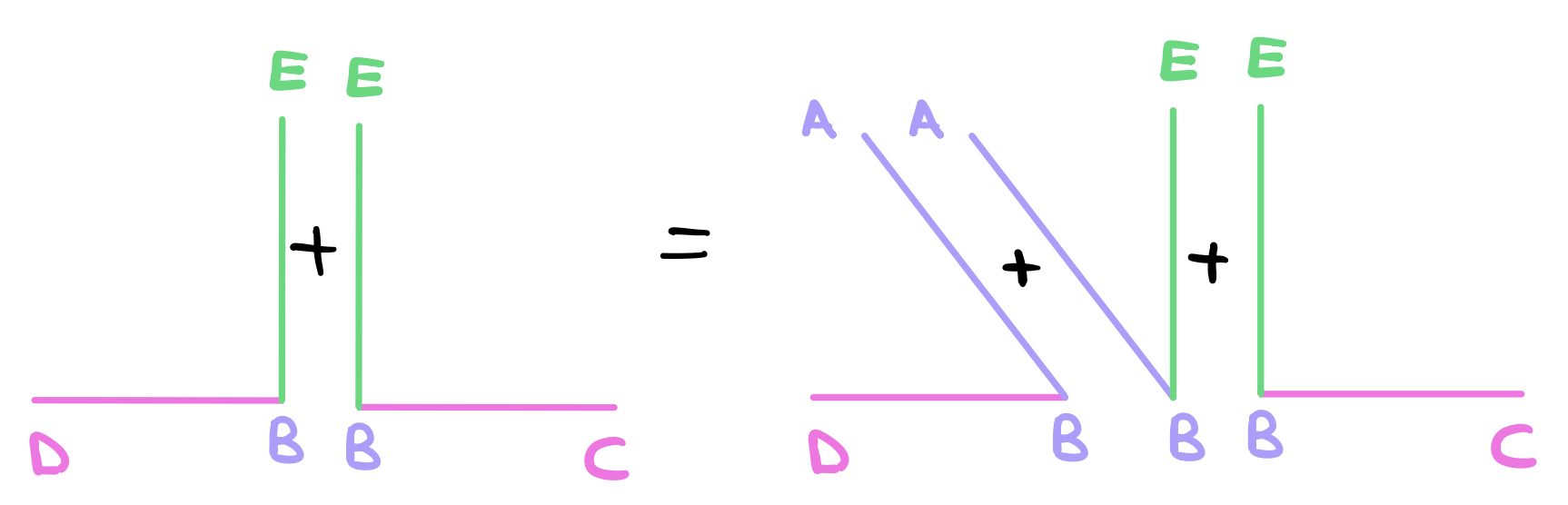
$$$$ \begin{align} \angle DBE &= \angle DBA + \angle ABE \\ \angle DBE + \angle EBC &= \angle DBA + \angle ABE + \angle EBC \end{align} $$$$

So angles $\angle DBE$ and $\angle EBC$ are equal to the three angles $\angle DBA$, $\angle ABE$ and $\angle EBC$. Similarly, the angle $\angle ABC$ is equal to the angles $\angle ABE$ and $\angle EBC$. Let the angle $\angle DBA$ be added to each.

$$$$ \begin{align} \angle ABC &= \angle ABE + \angle EBC \\ \angle ABC + \angle DBA &= \angle ABE + \angle EBC + \angle DBA \\ \end{align} $$$$

We can see that both $\angle ABC$ and $\angle DBA$ are equal to the three angle $\angle DBA$, $\angle ABE$ and $\angle EBC$.

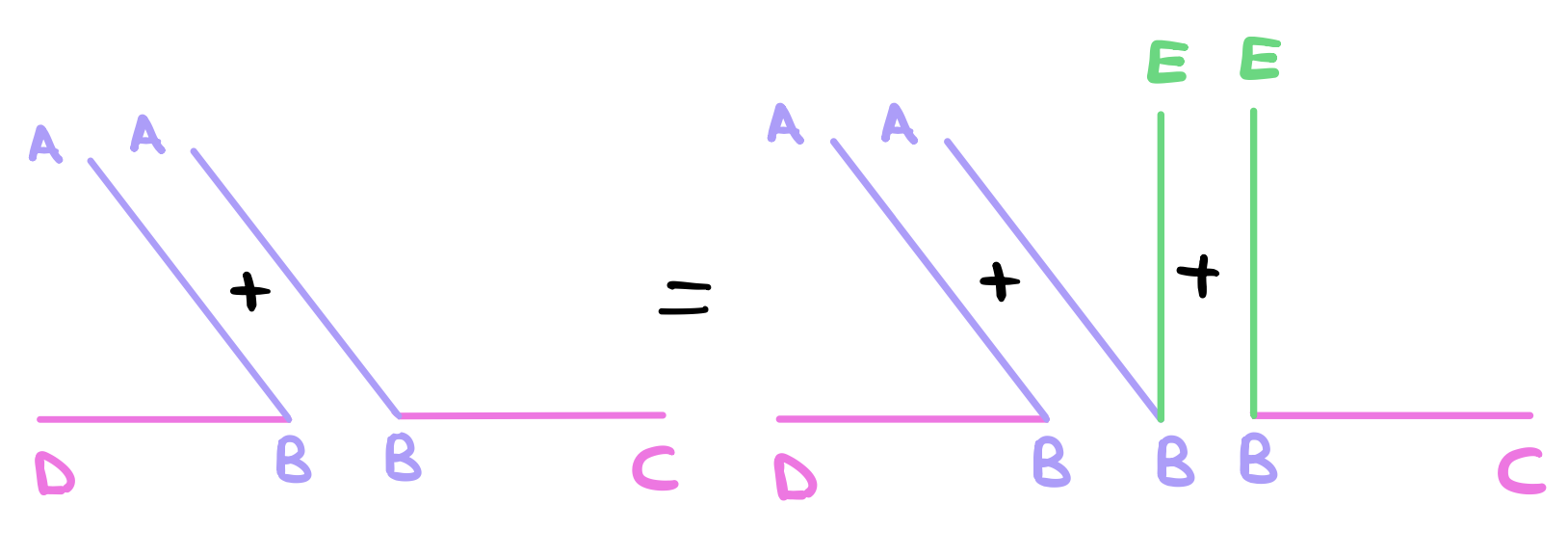
Finally, we can see from both equations that angles $\angle ABC$ and $\angle DBA$ and again angles $\angle DBE$ and $\angle EBC$ are both equal to the same three angles. By common notion 1, things which are equal to the same thing are also equal to one another. Therefore angles $\angle ABC$ and $\angle DBA$ are to equal angles $\angle DBE$ and $\angle EBC$. Since angles $\angle DBE$ and $\angle EBC$ are both right angles, then angles $\angle ABC$ and $\angle DBA$ are equal to two right angles as we claimed.

Thoughts: Even though it looked extremely straight forward, I definitely spent a lot of time repeating the angles over and over again in my head.

References: