Note

These are my rough notes based on attending CS148. They might contain errors so proceed with caution!

Why Triangles?

So why do we chose to render with triangles? So many benefits. Here are some:

If we only focus on one thing then we can optimize everything for just this one type (triangles). We can optimize software, algorithms, hardware (gpus) for just the triangles. For example, we can write the basic algorithms to manipulate triangles directly into the hardware.
Complex objects can be approximated very well with triangles when using enough triangles
Polygons can we always be divided into triangles.
Triangles are Planar. If you have three points, there is always a plane that goes through all three. This isn’t true for 4 points for example. So now we can simplify algorithms and make extra assumptions if we need to.
You only need to apply the transformation to the 3 vertices of the triangles and the whole triangle will just transform with it.
With triangles, we have barycentric coordinates. We can use them to interpolate and color the triangle from the inside to whatever we want.

Rasterization

So far we saw:

The process from creating geometry and then using transforms to place the geometry into the virtual world using matrix multiplications (rotations, scaling, translation).
After this, we transformed the geometry again but this time from world space to screen space using the projection matrix via matrix multiplication again.
So now, we need to find all the pixels inside this 2D screen space triangles and color them!

Step (3) is the Rasterization step where we find the pixels and color them. It’s expensive to find the pixels if we go and try every single pixel to test. There are mechanism to avoid testing all possible pixels. One technique is the bounding box technique where we limit the number of pixels to test to the bounding box of each triangle. Next we will need to test whether a pixel is inside a triangle (color it) or outside a triangle (don’t color). How do we do this? First we will need to study the implicit equation for a line.

Implicit Equation for a line

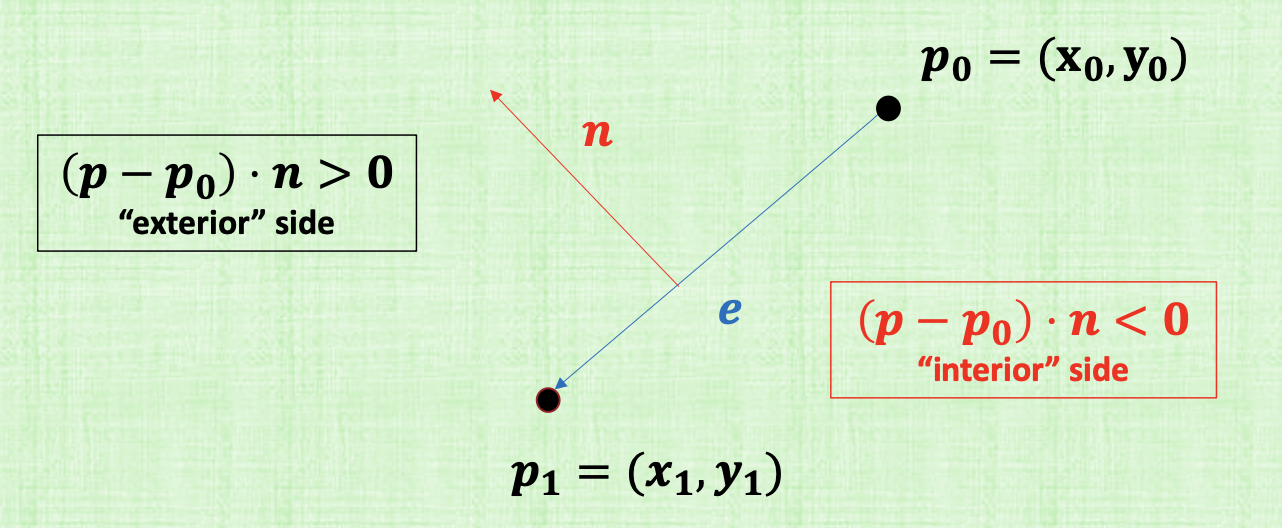
Given two points. $p_0$ and $p_1$:

Compute a direction $p1-p_0$.
Compute the normal. $n=y_1-y_0-(x_1-x_0)$.

This normal is the “rightward” normal with respect to the ray direction. This is the normal we will choose. This normal will divide the plane (or the 3d space) into two areas.

If $(p - p_0) \cdot n = 0$, then we’re on the line exactly.
If $(p - p_0) \cdot n > 0$, then $p$ is the right of the line with direction $p_1-p_0$. this means the point is on the exterior side. (the side where the normal is going to be the exterior side).
If $(p - p_0) \cdot n < 0$, then $p$ is on the left side of the line with direction $p_1-p_0$ (so going from $p_0$ to $p_1$). (clockwise).

IF we’re in 3D space, it will be very similar, points on top (where the normal is) and the points below the plane (opposite direction). This division of which area is exterior or interior is convention. We chose it the area where the normal is to be the exterior and the other area to be the interior.

2D Points Inside a 2D Triangle

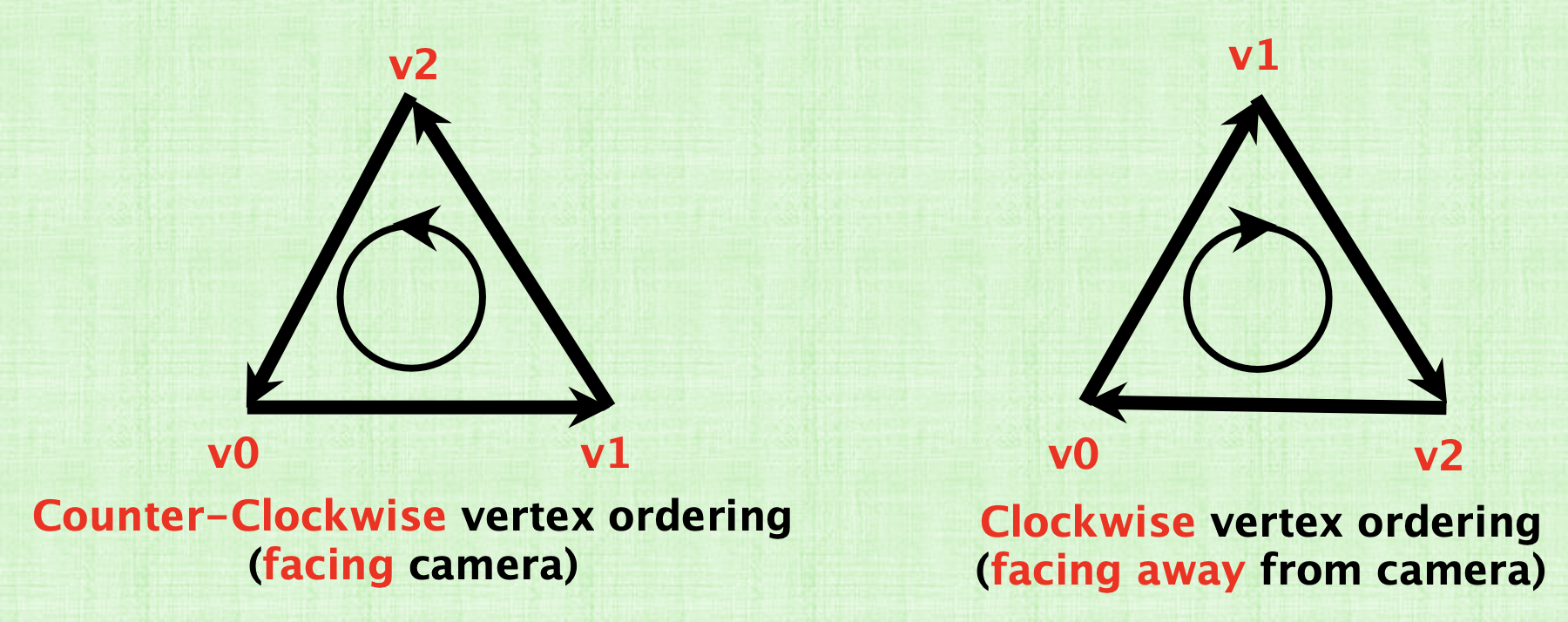
So given the convention we’ve decided. We have two cases for the order of vertices in triangles:

Counter clockwise vertex ordering (facing camera)
Clockwise vertex ordering (facing away from the camera)

So suppose we have the points $v_0, v_1, v_2$. By convention the edges are: $v_0v_1$, $v_1v_2$, $v_2v_0$. Also suppose that we’re currently testing a pixel $p$ that is inside the triangle. How do we test if it’s inside or outside the triangle? We’ll compute it’s dot product with the three normals for each edge.

If the vertices were ordered in a anticlockwise orientation, then if we walk from $v_0$ to $v_1$, the normal will be down and the interior is inside the triangle. So the product of $p$ with $n_0$, will negative and $p$ will be on the left of the edge that goes from $v_0$ to $v_1$. So $p$ is interior. Similarly, for the remaining two edges, we’ll find that $p$ is on the left of each edge and interior.
If the vertices were ordered in a clockwise orientation, then if we go form $v_0$ to $v_1$, the normal is on the right and that section will be the exterior part by convention. The dot product with the normal will be positive, So $p$ is on the right of the line where the normal is and is considered to be OUTSIDE the triangle. So we will NOT color it even though in reality it is in fact inside the triangle. This means that we won’t find any points inside and the triangle will be invisible!

This leads us to stress out the fact that vertex ordering matters: backward facing triangles are not rendered since no points are to the left of all three rays and to re-iterate: A point $p$ is considered inside a 2D triangle when it is interior (to left of all) all 3 rays.

Overlapping Triangles

When one object is in front of another, two triangles can aim to color the same pixel. We know that the screen space projection computes $z' = n + f - (fn/z)$ for occlusion/transparency so color each pixel using the triangle that has the smallest $z'$ at that pixel! The problem here is that we do know the $z'$ for each vertex of every triangle but what we want is the $z'$ for the exact pixel that we’re trying to color. For this reason we need to interpolate the vertices using the barycentric Coordinates) to find the $z'$ for that exact pixel. One other reason for doing this (instead of just picking one triangle over the other), is that these two triangles might intersect so you don’t want to choose one or the other. We want to the color the correct portion.

So we need to interpolate $z'$ values from triangle vertices to the pixel locations. in order to do this, we use “screen space barycentric weight interpolation”. How do we do this? There is a proper way and an improper way of calculating these barycentric weights.

Perspective Projection: Recap

So far we’re given a triangle $p_0,p_1,p_2$ and then we project it into screen screen to get $p_0',p_1',p_2'$ where the x-coordinate of each point is $x_i' = hx_i/z_i$ and the y-coordinate is $y_i'=hy_i/z_i$ for each vertex.

After the projection, we’re given a pixel at location $p'$ in screen space and we want to compute the color of the pixel. The triangle with the smallest $z'$ is used to shade the pixel. In order to find $z'$, we said that we need to compute the barycentric weights for the triangle we’re given, so $p' = \alpha_0'p_0' + \alpha_1'p_1' + \alpha_2'p_2'$ but this actually doesn’t work and $p'$ can’t be interpolated this way (unless the original triangle had the same z value for all three vertices). The reason why it doesn’t work is because when we project this triangle, we divide by $z$ and it deforms this triangle if it wasn’t flat.

To solve this, we have to do this calculation the right way. We’ll study the algebraic explanation and we’ll do the geometric one later in Texture Mapping. So what we want is to find if the current triangle I’m rendering has a z value which bigger or smaller than some other triangle.

The ray tracer won’t have a problem. It sends a ray. The ray intersects the triangle in the virtual world at some location $p$. We interpolate and we get the correct $z$ value. That works. But for $p'$ that doesn’t work. The triangle is distorted. This interpolated z’ doesn’t correspond to what’s in the virtual world. WHAT WE NEED is linear interpolation in world space NOT in the screen space. “The barycentric weights for the interior of a screen space triangle do not correspondingly describe the interior of its corresponding world space triangle”.

LOTS of CRAZY DERIVATION … TODO. but the summary is that the correct barycentric weights OF THE TRIANGLE IN WOLRD SPACE ARE:

$$ \begin{align*} \alpha_0 &= \frac{z_1z_2\alpha_0'}{z_1z_2\alpha_0'+z_0z_2\alpha_1'+z_0z_1\alpha_2'} \\ \alpha_1 &= \frac{z_0z_2\alpha_1'}{z_1z_2\alpha_0'+z_0z_2\alpha_1'+z_0z_1\alpha_2'} \\ \alpha_2 &= \frac{z_0z_1\alpha_2'}{z_1z_2\alpha_0'+z_0z_2\alpha_1'+z_0z_1\alpha_2'} \end{align*} $$

We can use this to compute $z = \alpha_0z_0 + \alpha_1z_1 + \alpha_2z_2$

Depth

For the pixel color, texture mapping and some other stuff we need to get the correct barycentric weights of the triangle in world space and not screen space (last section) BUT for the depth buffer we actually don’t need to do that!

So we know from the last section how to compute the correct barycentric coordinates in world space such as,

$$ \begin{align*} \alpha_0 = \frac{z_1z_2\alpha_0'}{z_1z_2\alpha_0'+z_0z_2\alpha_1'+z_0z_1\alpha_2'} \end{align*} $$

We also know that in world space $z$ can be interpolated using $\alpha z_0 + \alpha_1 z_1 + \alpha_2 z_2$. Therefore, we’re going to substitute these values in. Let’s see what we get,

$$ \begin{align*} z &= \alpha z_0 + \alpha_1 z_1 + \alpha_2 z_2 \\ z & = ( \frac{z_1z_2\alpha_0'}{z_1z_2\alpha_0'+z_0z_2\alpha_1'+z_0z_1\alpha_2'})z_0 + ..... \\ z &= \frac{z_0z_1z_2}{z_1z_2\alpha_0'+z_0z_2\alpha_1'+z_0z_1\alpha_2'} \\ \frac{1}{z} &= \frac{z_1z_2\alpha_0'+z_0z_2\alpha_1'+z_0z_1\alpha_2'}{z_0z_1z_2} \\ \frac{1}{z} &= \alpha_0' \frac{1}{z_0} + \alpha_1' \frac{1}{z_1} + \alpha_2' \frac{1}{z_2} \end{align*} $$

So we started with $\alpha$s in world space and now we have $1/z$ in terms of $\alpha$s from screen space! This means that we can correctly interpolate $1/z$ with screen space barycentric weights even though $z$ can’t be! We also know that $z'$ can be computed using $n + f - (fn/z)$ (from the prespective transformation matrix), so let’s substitute

$$ \begin{align*} z_i' &= n + f - \frac{fn}{z_i} \\ \frac{1}{z_i} &= \frac{n + f - z_i'}{fn} \\ \frac{1}{z_i} &= \frac{n + f - (\alpha_0z_0' + \alpha_1z_1' + \alpha_2z_2')}{fn} \\ \frac{1}{z_i} &= \frac{n + f - (\alpha_0z_0' + \alpha_1z_1' + \alpha_2z_2')}{fn} \end{align*} $$

……TODO….. We did all of this to prove that we can still compare $z'$ to find which triangle comes first. Even if the $z'$ values are deformed, we can still compare them to determine the ordering of the triangles. This is important since there will be a ton of triangles and we only we want to process the relavent ones. Once we get rid of the triangles that don’t matter, we now have to calculate the correct barycentric coordinates in world space to correctly interpolate the right colors.

References

Fundamentals of Computer Graphics, 4th Edition
CS148 Lectures