Note

These are my rough notes based on attending CS148. They might contain errors so proceed with caution!

Overview

The barycentric coordinates are heavily used to graphics. We typically work with triangles and so when we’re about to color a pixel we interpolate the values in the three vertices of the triangle to come up with the right color for the pixel. This applies to many other information stored at the vertices like reflectivity, transparency and so on. To define barycentric coordinates, we ‘ll start by studying the parametrized function form of a line segment next.

Parametrized Functions for Line Segments

How do we interpolate between two points on a line segment? use the parametric form. Suppose we have two points \((x_1,y_1), (x_2,y_2)\)

$$ \begin{align*} y(x) &= \frac{y_2-y_1}{x_2-x_1} (x - x_1) + y_1 \\ y(x) &= (1 - \frac{x-x_1}{x_2-x_1})y_1 + (\frac{x-x_1}{x_2-x_1})y_2. \end{align*} $$

So now let \(t=\frac{x-x_1}{x_2-x_1}\)

$$ \begin{align*} y(t) = (1-t)y_1 + ty_2. \end{align*} $$

This \(t\) ranges from 0 to 1 and can be seen as the fraction of the way from \(x_1\) to \(x_2\).

Barycentric Weights for Line Segments

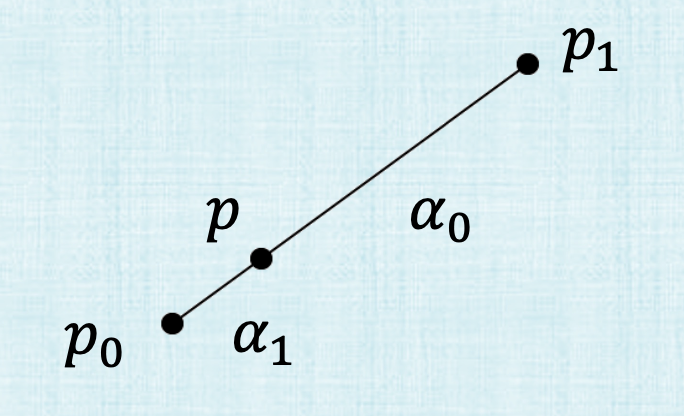
So that’s fine but really, we don’t care about the length among the axis. We care about the length along the segment itself. So instead of the parameter or the fraction being a fraction of the length along the x-axis, we want that to be a fraction of the length travel along the segment. So suppose we have two points \(p_0\) and \(p_1\), for

$$ \begin{align*} y(t) = (1-t)p_0 + tp_1. \end{align*} $$

We want \(t\) to be \(\frac{\left\lVert p-p_0 \right\rVert_2 }{\left\lVert p_1 - p_0 \right\rVert_2}\). which is the fraction of the distance from \(p_0\) to \(p_1\). Instead of \(t\) though, we want to reformulate this to use \(\alpha_0\) and \(\alpha_1\). \(t\) is \(\alpha_1\) and \(\alpha_0\) is \((1-t)\). \(\alpha_0\) and \(\alpha_1\) are the barycentric weights and we can now write,

$$ \begin{align*} p = \alpha_0 p_0 + \alpha_1 p_1. \end{align*} $$

with weights \(\alpha_0, \alpha_1 \in [0,1]\) and

$$ \begin{align*} \alpha_0 &+ \alpha_1 = 1\\ \alpha_0 &= \frac{\left\lVert p-p_0 \right\rVert_2 }{\left\lVert p_1 - p_0 \right\rVert_2}\\ \alpha_1 &= \frac{\left\lVert p-p_1 \right\rVert_2 }{\left\lVert p_1 - p_0 \right\rVert_2}. \end{align*} $$

so again the alphas are the barycentric weights. and this whole process is called the barycentric interpolation. Note where \(\alpha_0\) and \(\alpha_1\) are on the line. We did as a convention. We could switch if we need to but it will make the next topic easier this way.

Barycentric Weights for Triangles (1st Approach: Geometric)

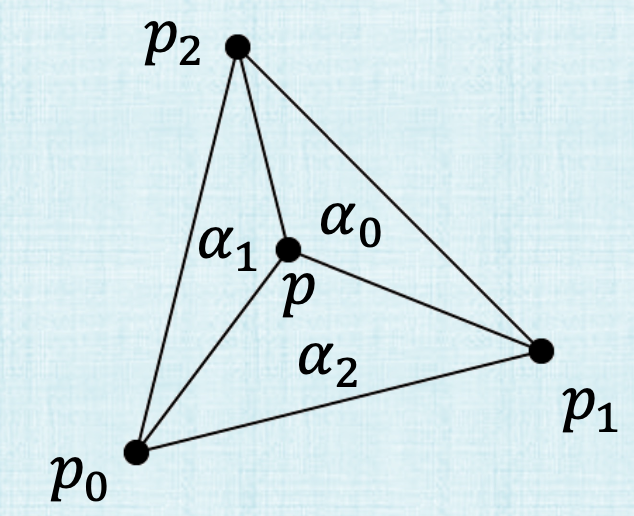
So for triangles we will express a point \(p\) as \(p = \alpha_0 p_0 + \alpha_1 p_1 + \alpha_2p_2\) with barycentric weights \(\alpha_0, \alpha_1, \alpha_2 \in [0,1]\) and \(\alpha_0 + \alpha_1 + \alpha_2 = 1\) We can compute the weights via the areas such as:

$$ \begin{align*} \alpha_0 &= \frac{ Area(p, p_1, p_2) }{p_0, p_1, p_2} \\ \alpha_1 &= \frac{ Area(p, p_0, p_2) }{p_0, p_1, p_2} \\ \alpha_2 &= \frac{ Area(p, p_0, p_1) }{p_0, p_1, p_2}. \end{align*} $$

So \(\alpha_0\) for example is made by the area that doesn’t involve the vertex \(p_0\) divided by the whole area of the triangle (\(p_0, p_1, p_2\)) which can be computed by

$$ \begin{align*} Area(p_0, p_1, p_2) &= \frac{1}{2} \left\lVert p_0p_1 \times p_0p_2 \right\rVert_2 \end{align*} $$

So using the cross product, we can compute all these areas to derive the barycentric coordinates.

Barycentric Weights for Triangles (2nd Approach: Algebraic)

TODO



Barycentric Weights for Triangles (3rd Approach)

Compute the vectors \(u = p_0 - p_2\) and \(v = p_1 - p_2\). Any point \(p\) in the triangle can be written as

$$ \begin{align*} p = p_2 + \beta_1 u + \beta_2 v. \end{align*} $$

with \(\beta_1, \beta_2 \in [0,1]\) and \(\beta_1 + \beta_2 \leq 1\). Substitue back \(u\) and \(v\) to see that,

$$ \begin{align*} p = \beta_1 p_0 + \beta_2 p_2 + (1 - \beta_1 - \beta_2)p_2. \end{align*} $$

where \(\alpha_0 = \beta_1\), \(alpha_1 = \beta_2\) and \(\alpha_2 = 1 - \beta_1 - \beta_2\).

Find the color and z' value at a pixel

To see an example, let’s say we want to find the \(z'\) of a pixel. we know the \(z'\) value for each vertex of the triangle. What do we do now? We just figure out the barycenteric weights and multiply the weights by the \(z'\) values of each vertex of the triangle in,

$$ \begin{align*} z' = \alpha_0 z_0' + \alpha_1 z_1' + \alpha_2z_2' \end{align*} $$

Similarly we can interpolate the color of the pixel. Multiply the color of the vertices by their the barycentric weight to find the exact color of the pixel.

References

CS148 Lectures