A set of points \(S\) is convex if for any two points \(a \in S\) and \(b \in S\), then the line segment connecting these two points is also in \(S\) (\(\overline{ab} \subseteq S\)). The convex hull of \(S\) is the smallest convex set that contains all the points in \(S\). In the previous post we discussed Jarvis’s algorithm which picked an initial vertex and added it to the convex hull and then iterated over the remaining vertices. In each iteration, we picked and added to the hull the furthest to the right vertex relative to the last added vertex to the hull. The running time of Jarvis’ March is \(O(nh)\) where \(n\) is the size of the given set of points and \(h\) is the size of the convex hull. In this post, we will learn a faster algorithm that runs in time \(O(n\log n)\).
Graham's Scan
Given a set of points \(S\) of size \(n\), the idea is to pick a point \(p_0\) from the set that is known to be in the convex hull and then sort the remaining points by their angle anti-clockwise relative to \(p_0\). Graham gave a linear-time algorithm to find vertex that is interior to the hull but this isn’t needed at all since we can just pick the lowest or left most vertex and know that all the remaining vertices will be on one side of the line that goes through the point. After picking an initial point, the algorithm will sort the remaining points anti-clockwise around the initial point by their angle. The core of the algorithm then is to use a stack to maintain the convex hull. We’ll iterate over the vertices keeping the invariant that for any three consecutive vertices on the stack \(p\), \(q\) and \(r\), the point \(r\) is on the left of the line that goes through the segment \(\overline{pq}\). In other words, the angle at \(q\) is a convex angle and not a reflex one. In the next few sections we’ll study each step through an example.
Step 1: Pick the Left Most Point
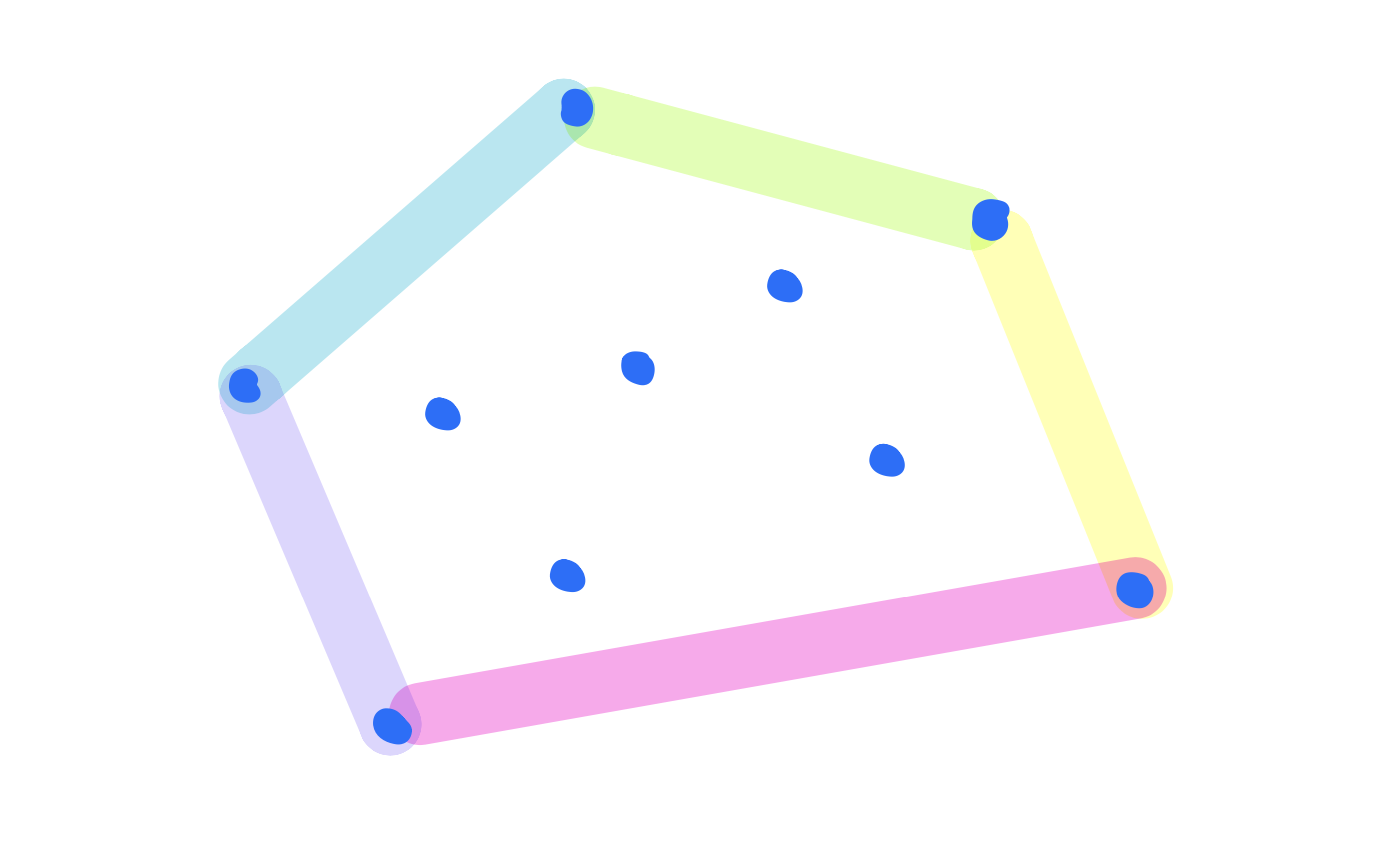
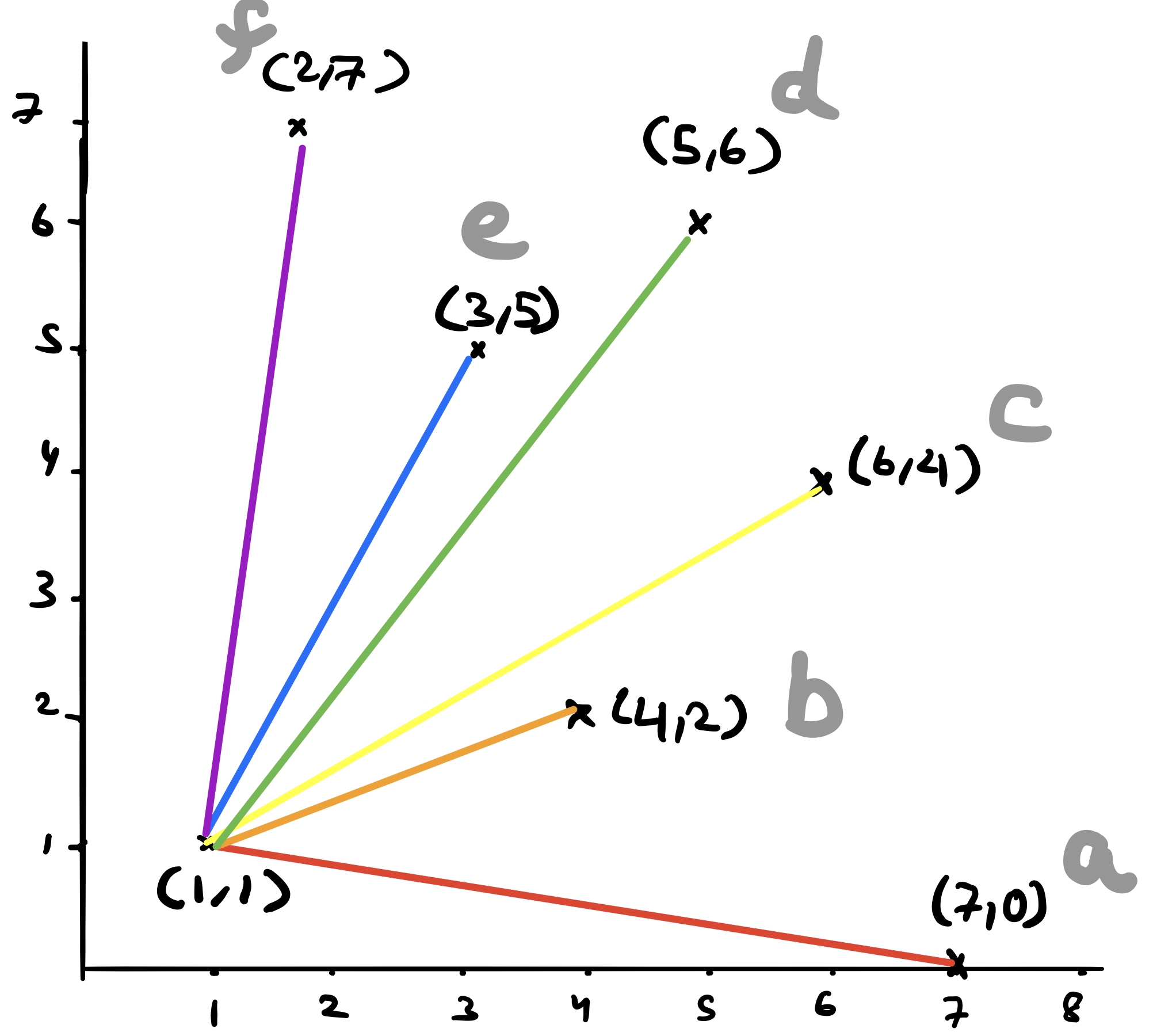
The best way to learn this algorithm is by following an example. Suppose we are given the below 7 points,
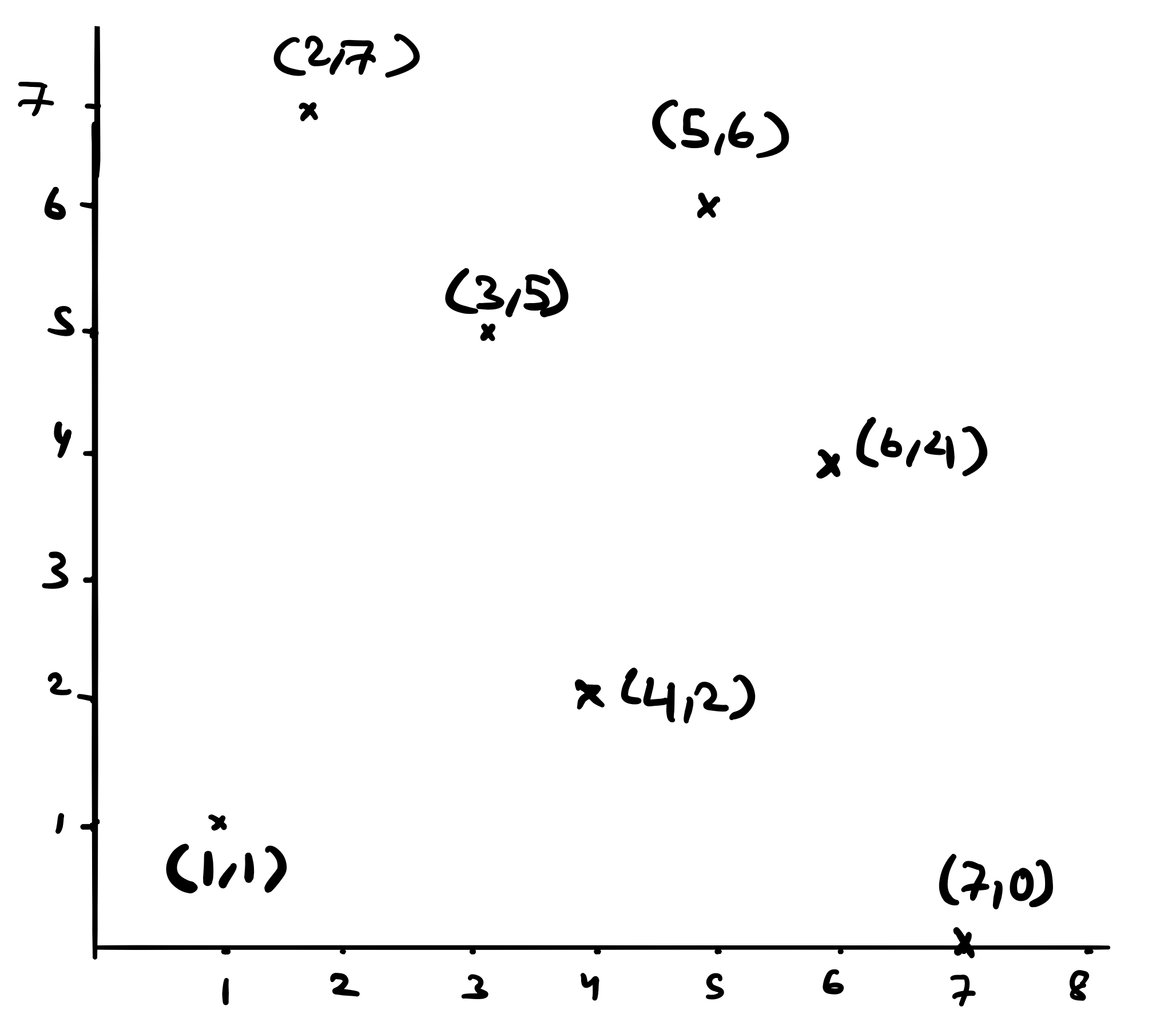
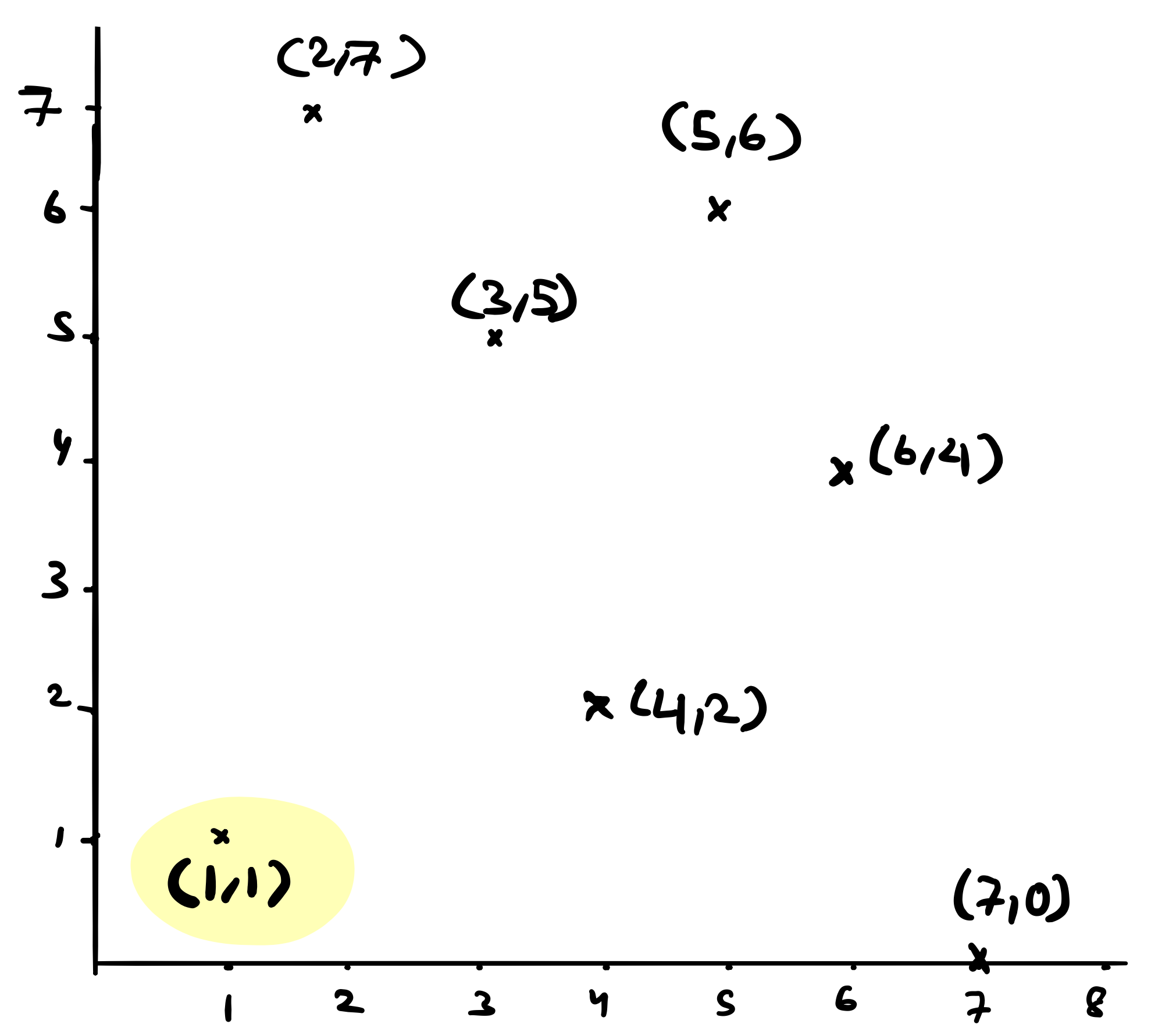
The first thing that the algorithm does is pick the left most point breaking ties by choosing the point with the lowest y-coordinate. This turns out to be point \((1,1)\) below
In the implementation, we do something like this
Point left_most = points[0];
for (int i = 1; i < points.size(); i++) {
if (points[i].x < left_most.x || (points[i].x == left_most.x && points[i].y < left_most.y)) {
left_most = points[i];
}
}
Step 2: Sort the Points
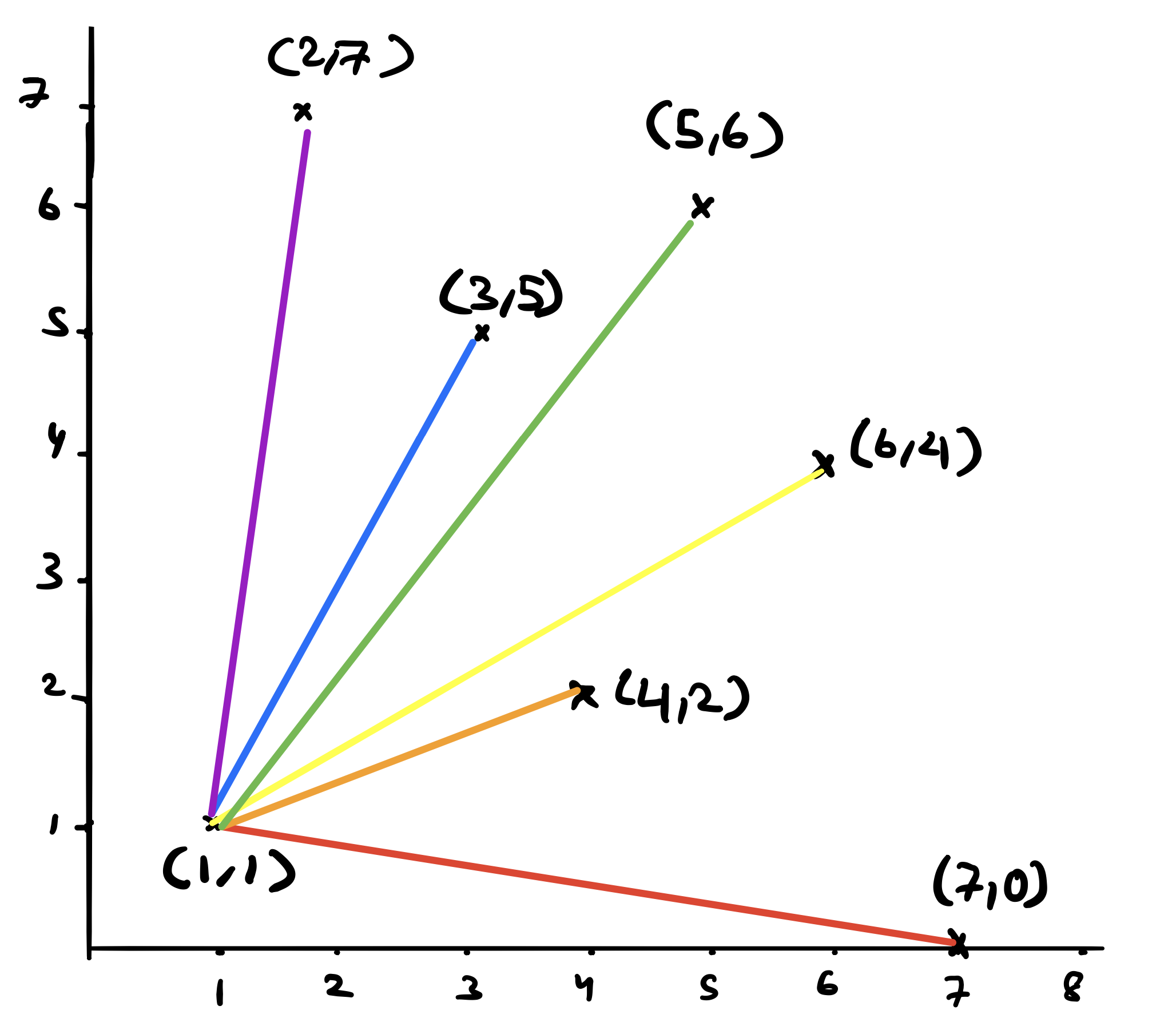
Next we will sort the points by their angle (anti-clockwise) around \((1,1)\). What does this mean? We’re not changing where the points are. We’re just changing the order in which we will process these points. What we want is to traverse the points in an anti-clockwise direction around \((1,1)\). So we want to start with the point that is furthest to the right from \((1,1)\) (remember that this is the left most point and there won’t be points anymore on the left). Therefore, if you imagine \((1,1)\) connected with line segments to each of the remaining points, then what we want is to sort these by the angles they make around \((1,1)\).
How do we sort by their angels? We will use the famous orientation test we’ve studied in (Orientation of Three Points). To recap, Suppose we’re given three ordered points \(p, q, r\), then the expression (derived from slopes) \((q_x-p_x)(r_y-p_y) - (r_x-p_x)(q_y-p_y)\) is
- Greater than zero when the slope of \(pq\) is smaller than the slope of \(pr\) and so the ordered points \(p, q\) and \(r\) are in anti-clockwise orientation and \(r\) is on the left of the line \(pq\)
- Equal to zero if they're collinear
- Less than zero when the slope of \(pq\) is greater than the slop of \(pr\) and so the ordered points \(p, q\) and \(r\) in a counter clockwise orientation and \(r\) is on the left of the line \(pq\)
This means that if we take the points \((1,1), (7,0)\) and \((4,2)\) and we want to know if \((4,2)\) comes before \((7,0)\) in the sorted order, then we’ll ask the question: “Is \((4,2)\) on the left of the line that goes through \((1,1)\) and \((7,0)\) ? if the answer is yes then \((4,2)\) should instead come after \((7,0)\). Evaluating the expression for \(p=(1,1), q=(7,2)\) and \(r=(4,2)\), we see that \(\)(7-1)(2-1) - (4-1)(0-1) = 6 - (-3) > 0\(\). Therefore, then we know that \((4,2)\) is on the left and in the sorted order, \((7,0)\) must come first.
How do we break ties? One example would be to choose the closest point between the two based on their distances to “left_most”. The final output will be the following (sorted points from \(a\) to \(f\)).
In the implementation, this is an example of how one might write the orientation function.
int orientation(Point a, Point b, Point c) {
long long area = (b.x - a.x)*(c.y - a.y) - (c.x - a.x)*(b.y - a.y);
if (area < 0) {
return -1; // cw
} else if (area > 0) {
return 1; // ccw
}
return 0;
}And this is how we can sort the array using \(std::sort\),
sort(points.begin(), points.end(), [&left_most](const Point& a, const Point& b) {
int d = orientation(left_most, a, b);
if (d > 0) { // ccw
return true;
} else if (d == 0) { // collinear
return distance(a, left_most) < distance(left_most, b);
}
return false;
});
Step 3: The Main Loop
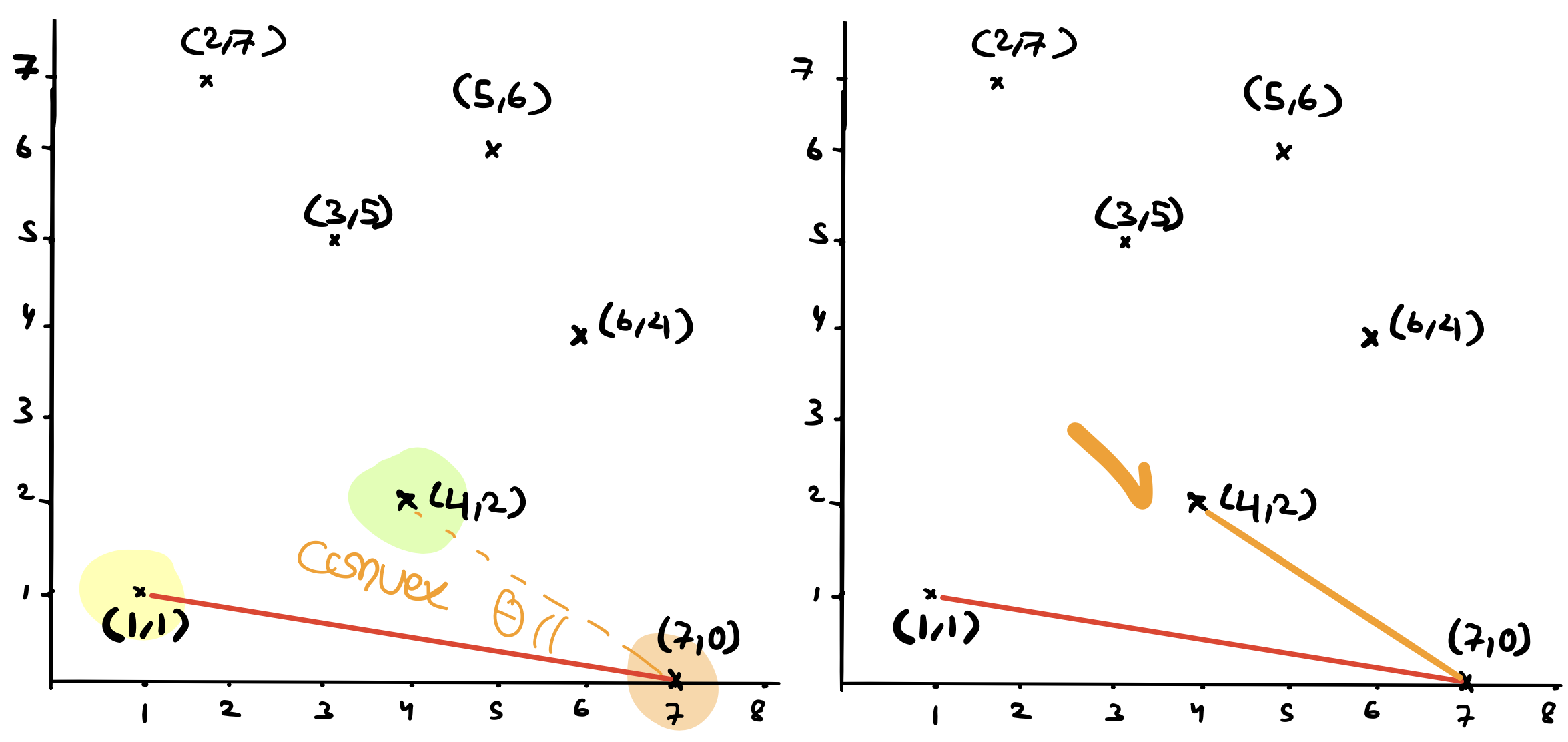
So now we have an initial point picked and we have the points sorted around it. Next, we will use a stack \(s\) to hold the hull points. Initially, \(s\) will hold the first two vertices in the sorted list of points, \((1,1)\) and \((7,0)\). Notice that \((1,1)\) and \((7,0)\) will be on the convex hull. \((1,1)\) is the left most point and \((7,0)\) is the point furthest to the right from \((1,1)\). (proof?).
Step 3: (Iteration 1)
Next we’ll iterate over the remaining points. In the first iteration we will test \((4,2)\). Let the last vertex added to the stack be \(q\) and the vertex that was added before that be \(p\). Let \(r=(4,2)\). We need to test if \(q\) is a convex vertex or in other words that \(r\) is on the left of the line that goes through \(\overline{pq}\) (we are making a left turn on \(q\)). How can test this? by performing yet another orientation test! Since \((4,2)\) is indeed on the left of the line, then it is safe to add it to the stack.
Step 3: (Iteration 2)
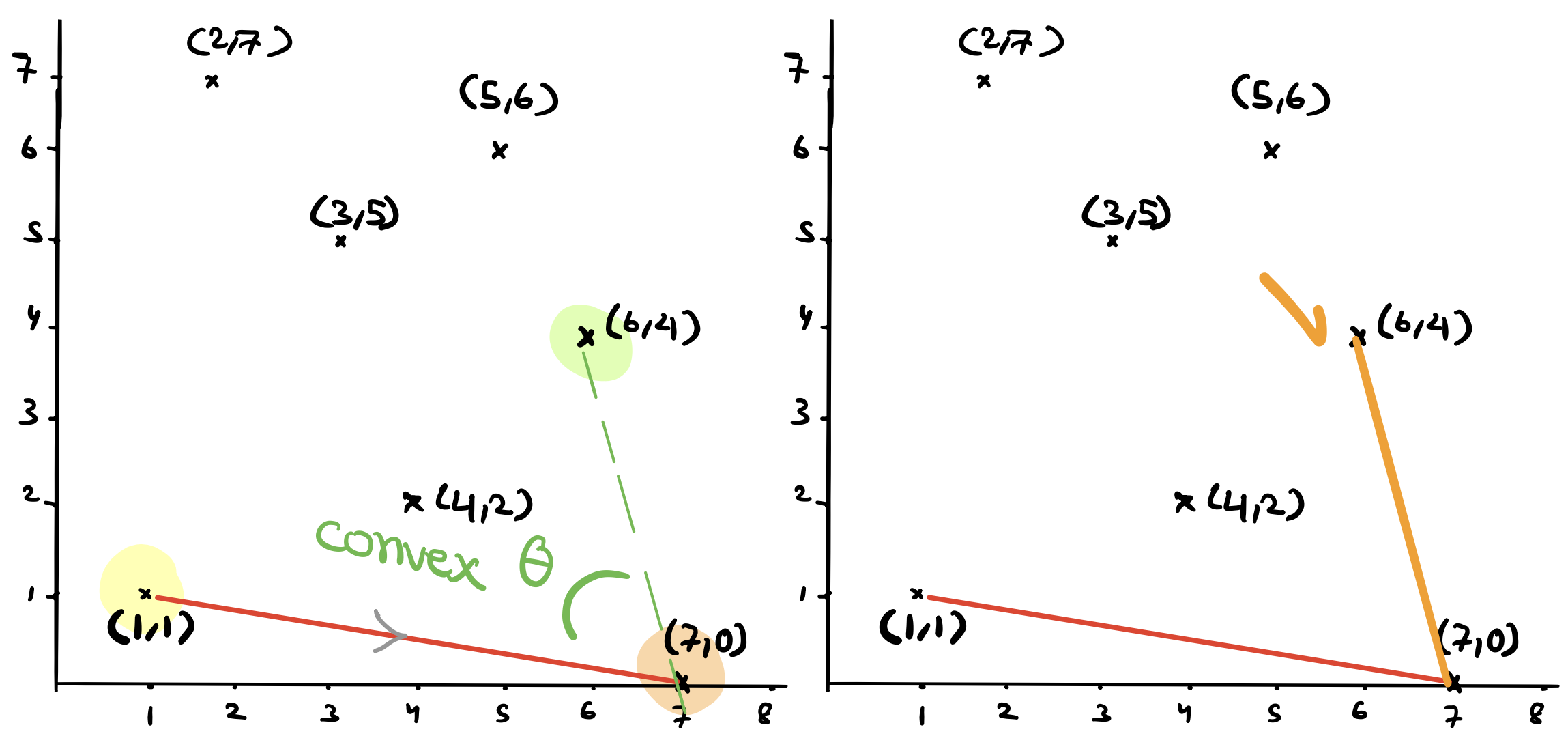
Next we will test \((6,4)\) against the last two vertices added to the stack. This time they are \(q=(4,2)\) and \(p=(7,0)\). Is \(r=(6,4)\) on the left of the line that goes through \((7,0)\) and then \((4,2)\). No! it is not. In this case, Graham will pop the last vertex we added to the stack which was \(q=(4,2)\).
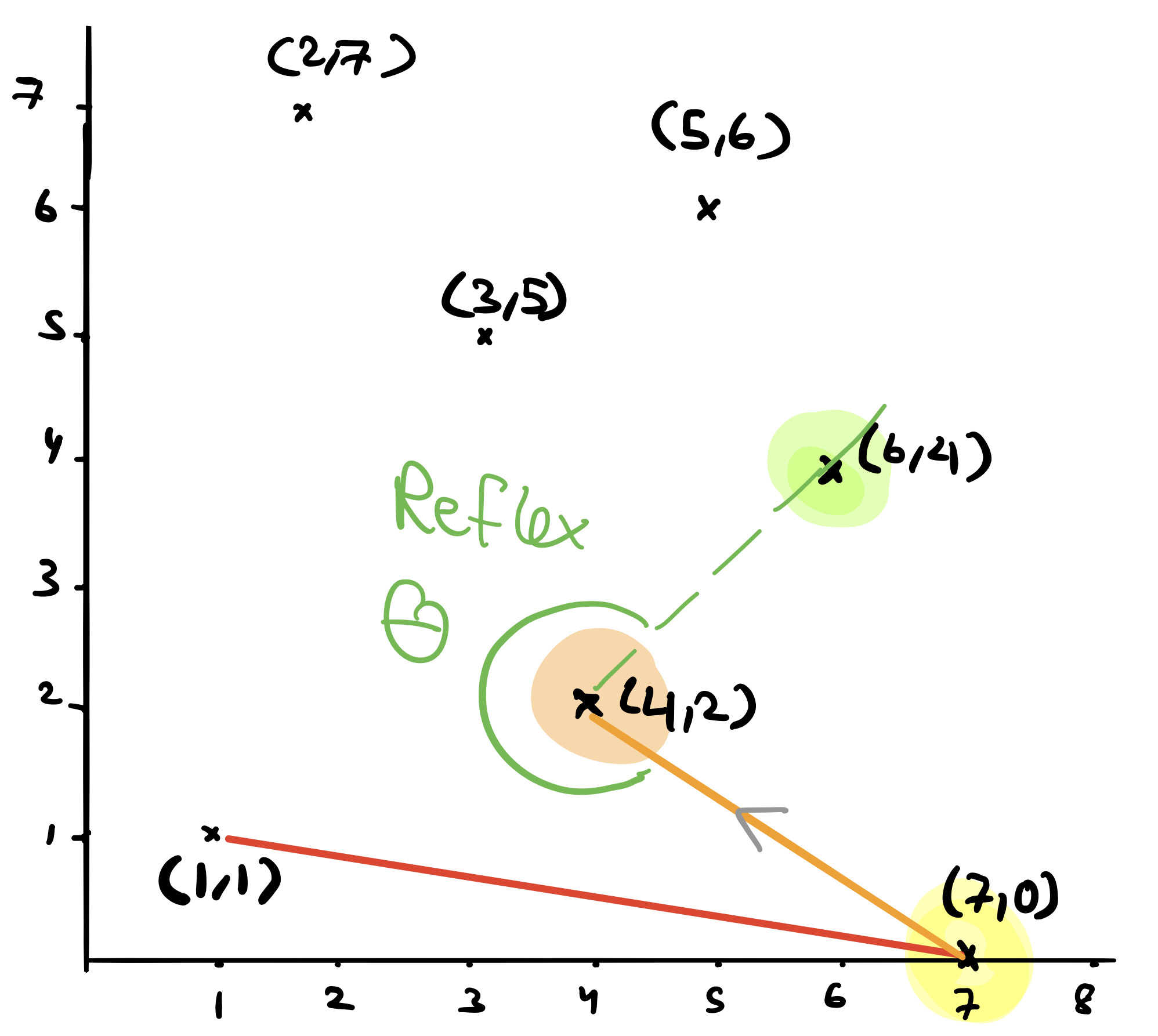
But now we not exit this iteration yet because we want to give the new point \((6,4)\) another chance. This time however, we will test \((6,4)\) against the current last two points on the stack which are \((7,0)\) and \((1,1)\). We will find that \((6,4)\) is on the left of the line that goes through \((1,1)\) and \((7,0)\) and we will add it to the stack. At this point, we can exit the iteration.
Step 3: (Iteration 3)
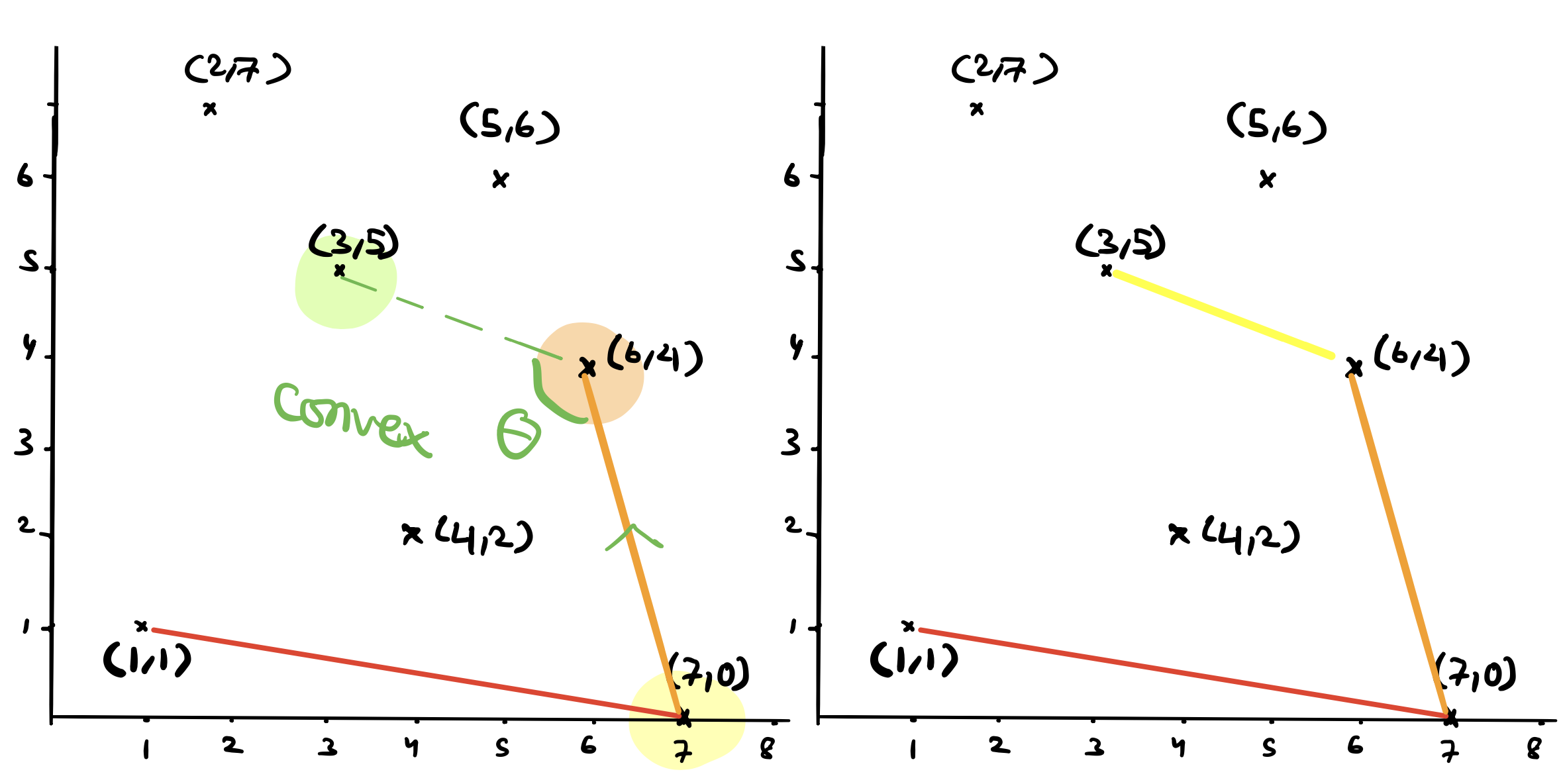
In the next iteration, we will test \((3,5)\). The last two points in the stack are \((6,4)\) and \((7,0)\). Is \((3,5)\) on the left of the line that goes through \((7,0)\) and \((6,4)\)? Yes! so we add \((3,5)\) to the stack.
Step 3: (Iteration 4)
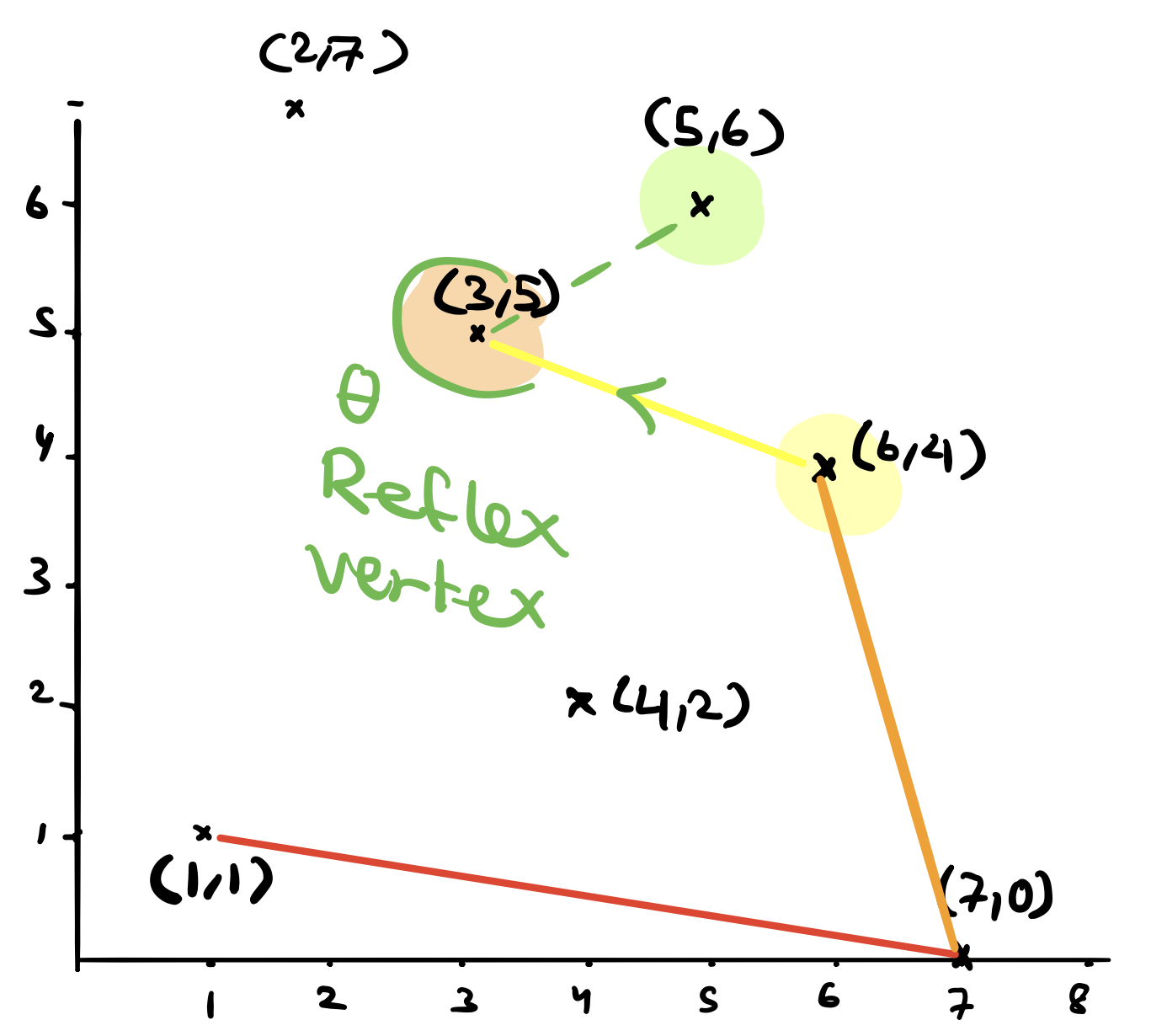
Next, we will test \((5,6)\). Is \((5,6)\) on the left of the line that goes through \((6,4)\) and then \((3,5)\)? No! \((5,6)\) is on the right and therefore, we now pop \((3,5)\) from the stack.
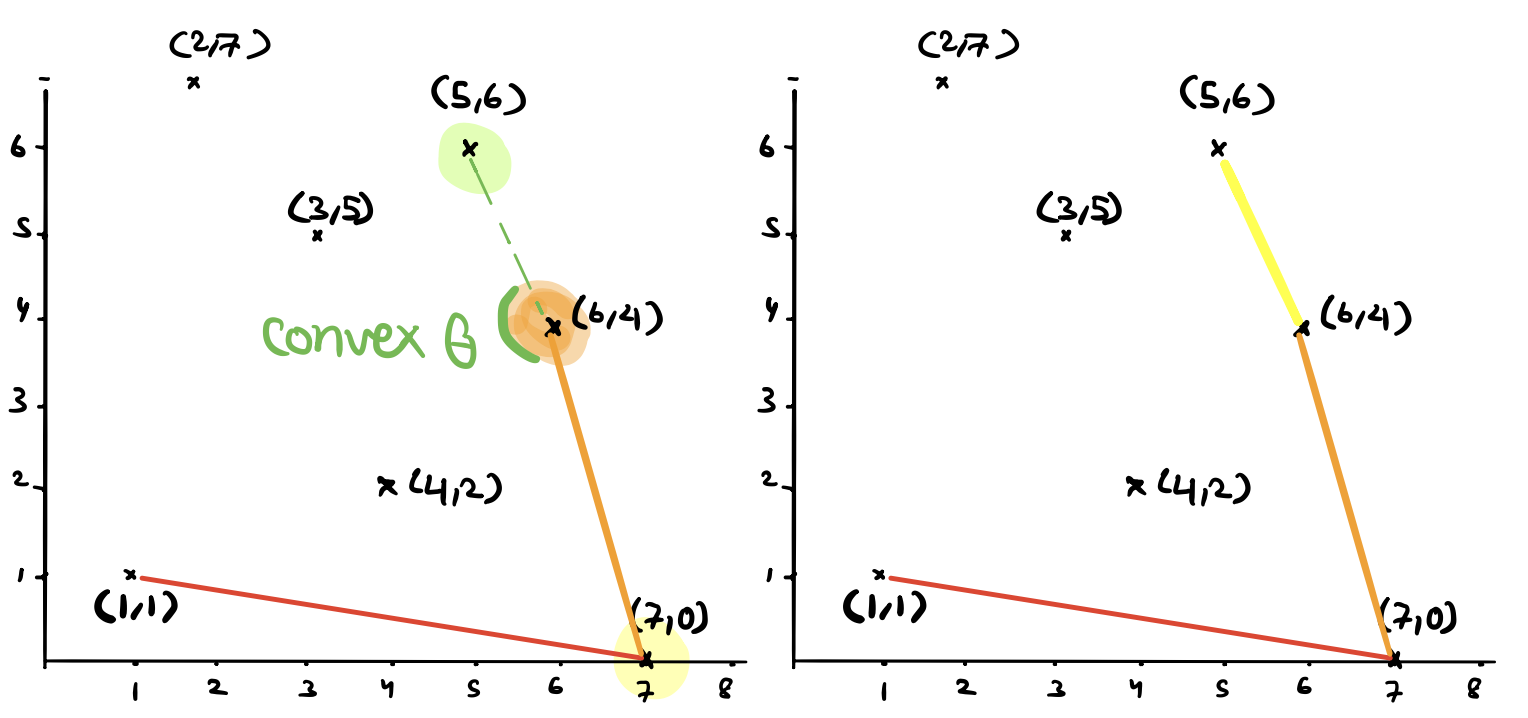
After popping \((3,5)\), we remain in the same iteration but now we test \((5,6)\) with current last two points on the stack \((6,4)\) and \((7,0)\). We will see that \((5,6)\) does validate the invariant and the vertex is still convex at \((6,4)\).
Step 3: (Iteration 5)
The last remaining point left in the array is \((2,7)\). We will perform the same test and find that indeed \((2,7)\) can be added to the stack.
style="text-align:center;">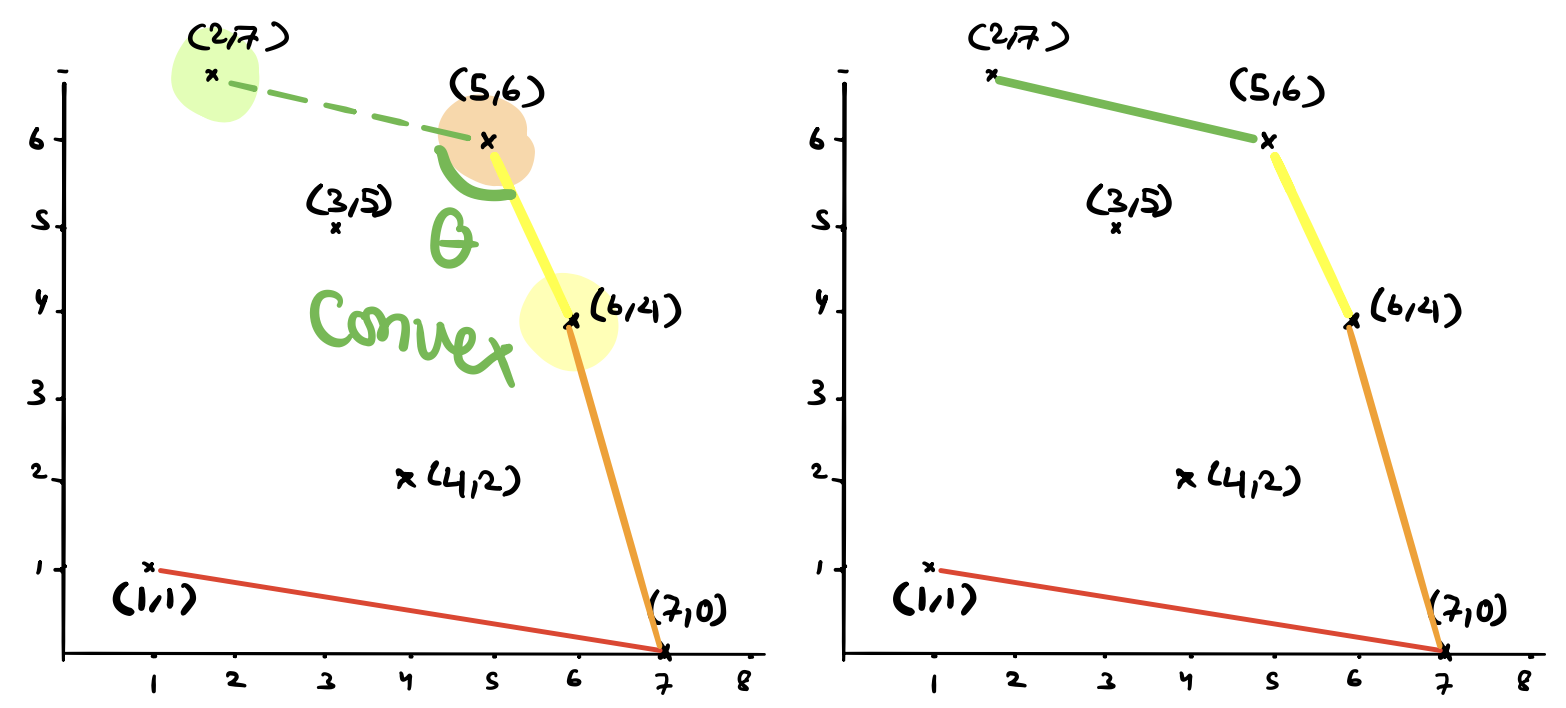
Step 3: Recap
Let’s summarize what we did so far. In each iteration, we will test vertex \(i\) with the last two vertices in the stack. Let the top most vertex be \(q\) and the second top most vertex be \(p\). We will then use the orientation test on \(p, q\) and \(r\).
- If test is positive and \(r\) is indeed on the left, then we'll push \(r\) on the stack and move to the next iteration.
- If the test is negative and \(r\) on the right, then we'll pop \(q\) from the stack and repeat the same test (though now we'll have different \(q\) and \(p\) vertices).
One possible implementation is the following
std::vector<Point> stack;
// The first two vertices are guaranteed to be on the hull
stack.push_back(left_most);
stack.push_back(points[1]);
// starting from the 3rd point,
for (int i = 2; i < (int)points.size(); i++) {
// let p = stack[stack.size()-2], q = stack[stack.size()-1], r = points[i]
// if r is on the right, of the line pq, then pop q and repeat the same test
// though now with a different p and q points
while (stack.size() > 1 && strict_right(stack[stack.size()-2], stack[stack.size()-1], points[i])) {
stack.pop_back();
}
// otherwise, r is on the left so just push it on the stack
stack.push_back(points[i]);
}
Collinear Points
What do we do with the collinear points? It depends. If we don’t care about collinear points and don’t want to output them, then instead of using “strict_right” above, we will use “right” to disallow collinear points from getting added to the stack. If we care and want to output all collinear points, then we’ll need to do some additional processing. I really struggled with understanding this myself so let’s show this with an example.
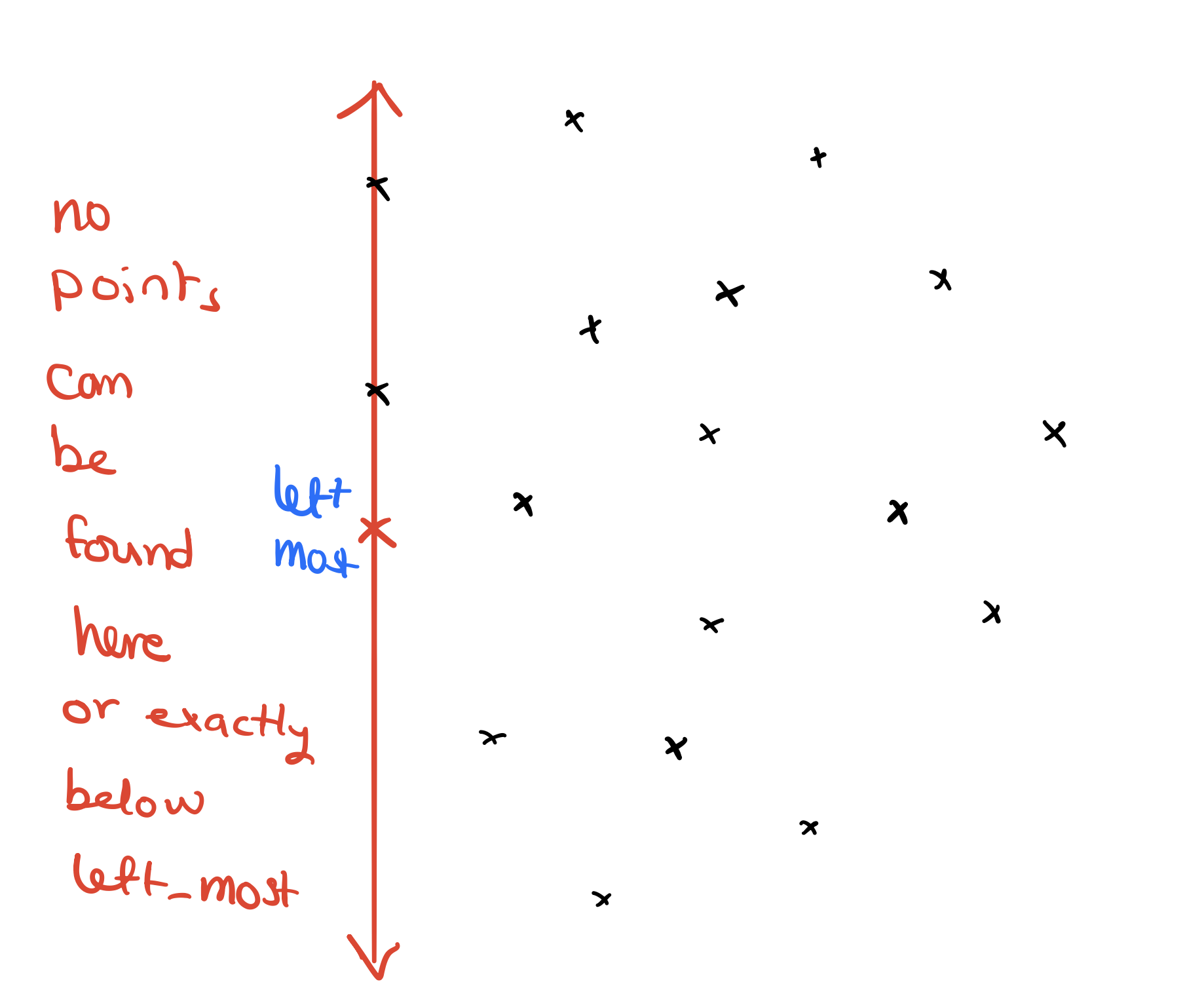
Suppose we are given the following points. We know per the algorithm we designed that no points are going to be located either on the left of “left_most” nor directly beneath it and this is because we break ties with picking the lowest y-coordinate.
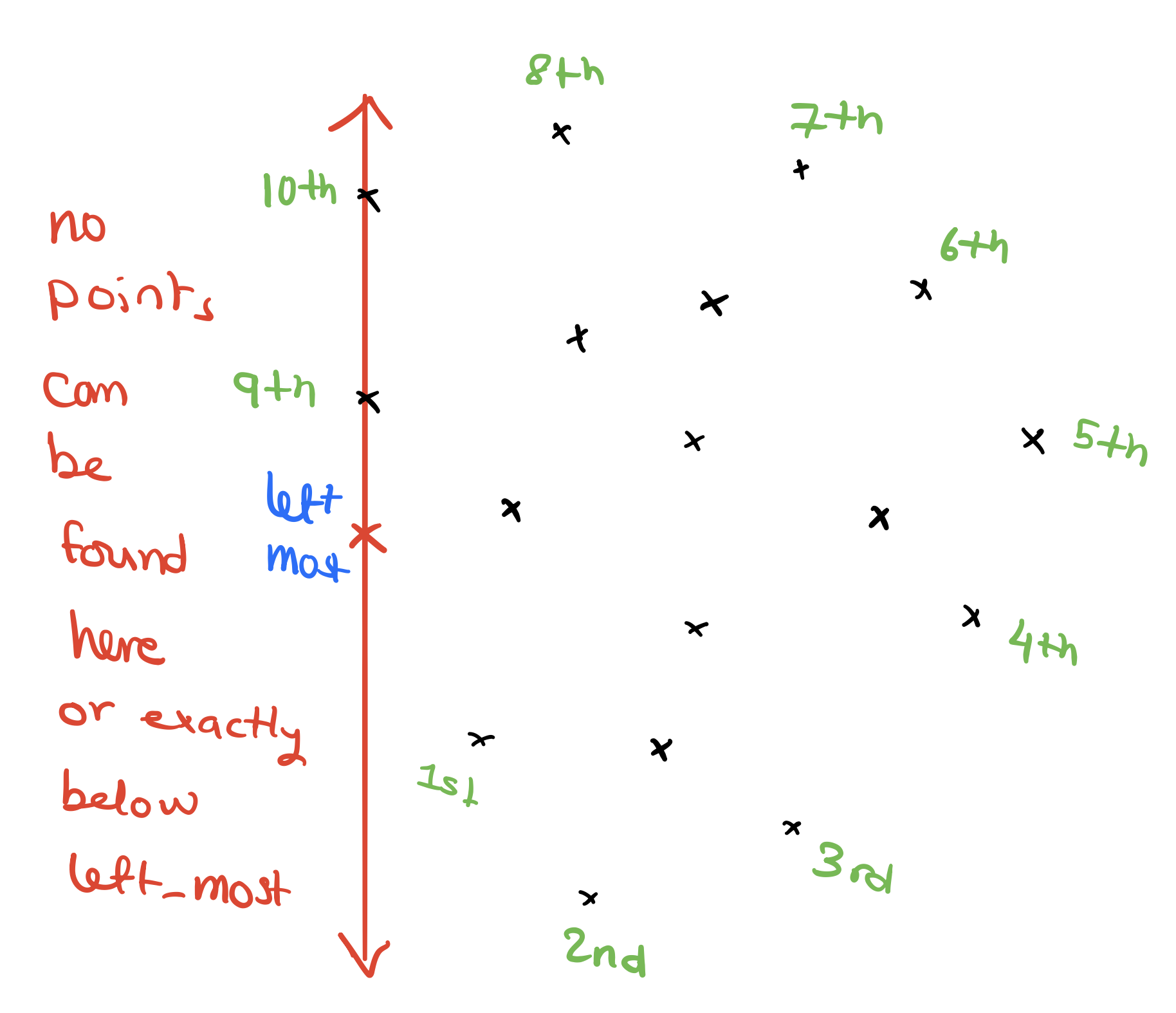
Next, we sort the points around “left_most” so that we will traverse the points from the most right point (smallest angle) to the most left point. I labeled the points with their traversal order. Also note here that we break ties based on the distance to “left_most”. The 9th and 10th points have the same angle but the 9th point is closer to “left_most” than the 10th point.
Next, we will proceed with the main loop, adding one vertex to the stack each iteration.
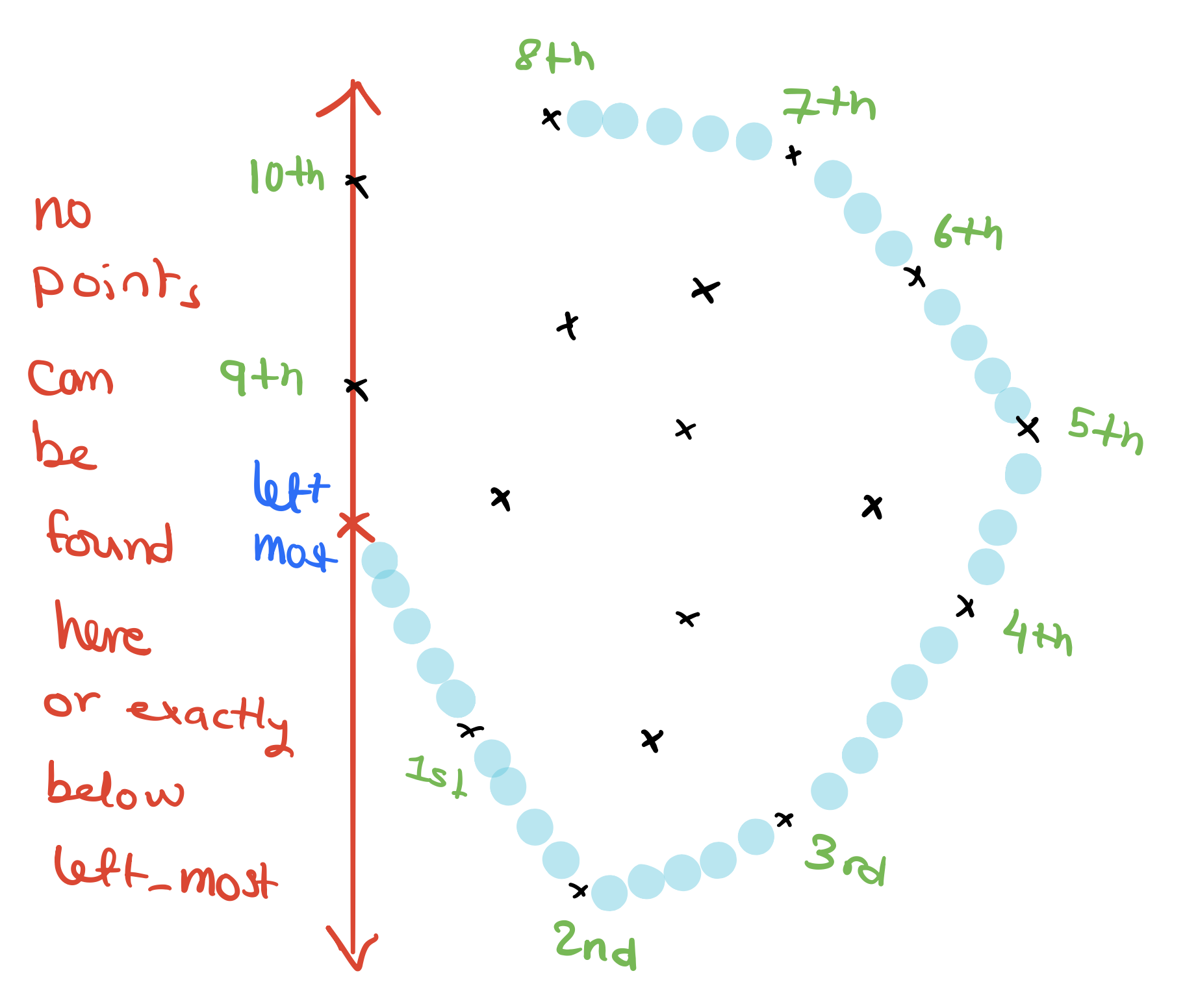
When we add the 10th point to the stack, notice that the 10th point is now on the right of the line that goes through the 8th and 9th points and therefore we don’t add it and exit the loop.
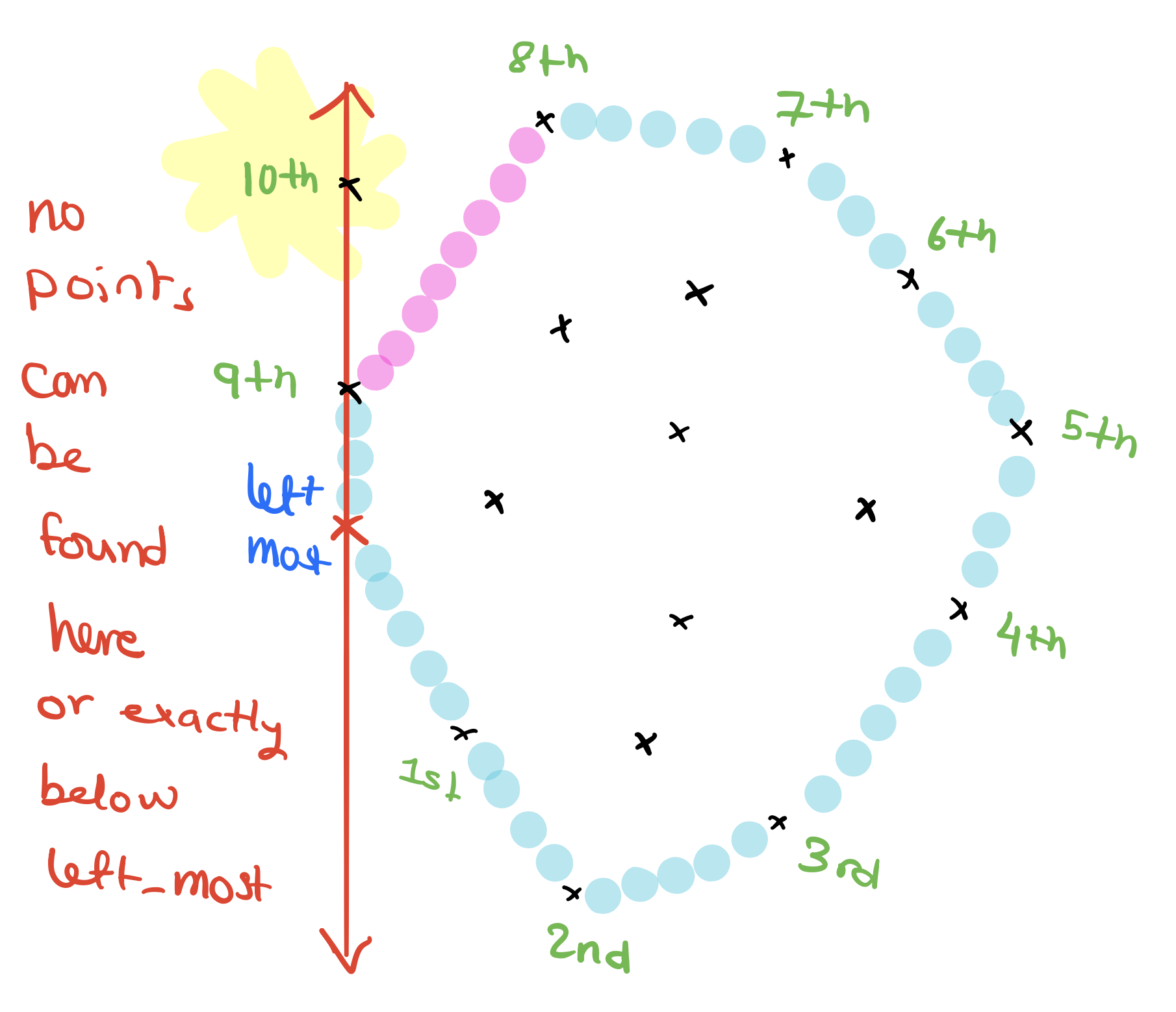
How do we fix this? We fix this by reverse sort the very last collinear points in the sorted array such that the closest point to “left_most” is actually the last point in the sorted order. This will allow us to test the 10th point first before the 9th point. We can simply do this using:
int i = (int)points.size()-1;
while (i >= 0 && collinear(left_most, points[i], points.back())) {
i--;
}
reverse(points.begin()+i+1, points.end());
Full Implementation
Source Code 11626 - Convex Hull
Practice Problems