In this note, I want to revisit the master theorem along with its proof outline as I’ve learned it in CS161 at Stanford (Professor Mary Wootters).
The Master Theorem
Let \(T(n) = aT(\frac{n}{b})+O(n^d)\) be a recurrence where \(a \geq 1\) and \(b \geq 1\). Then,
If this recurrence represents the running time of an algorithm then,
- \(a\) is the number of subproblems.
- \(b\) is the factor by which the input is decreasing at each level of the recursion.
- \(n^d\) is the total time needed to create the subproblems and combine their solutions.
Example
We can apply the master theorem on many recurrences. For example, if we’re given,
We can quickly see that we have \(a = 4\), \(b = 2\) and \(d = 1\). Therefore, \(a > b^d\) and so by using the master theorem, we can see that \(T(n) = O(n^{\log_2(4)}) = O(n^2)\).
Intuition
Why do we have 3 cases and what’s the intuition behind each case? To see this, we discuss three examples, one for each case, starting with case 2.
Case 2:
Clearly by the master theorem (case 2), the solution should be \(O(n)\). Intuitively, we’re reducing the size of each subproblem by half at each level of the recursion and at the same time, the decrease in the number of subproblem is more than the increase in the number of subproblems. So, the work is dominated by the top level of the recursion tree.
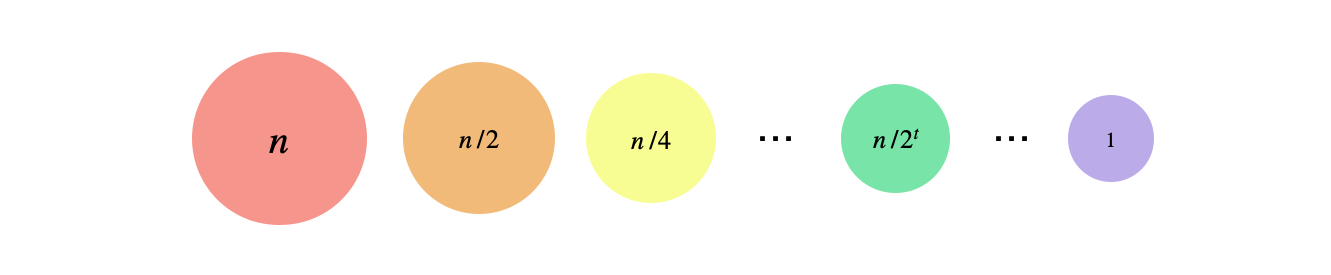 To be precise, we sum all the work done across all levels and use the geometric series \(\sum_{t=0}^{N}x^t = \frac{x^{N+1} - 1}{x - 1}\).
To be precise, we sum all the work done across all levels and use the geometric series \(\sum_{t=0}^{N}x^t = \frac{x^{N+1} - 1}{x - 1}\).
Case 3:
Again by the master theorem (case 3), the solution should be \(O(n^2)\). Intuitively, we’re reducing the size of each subproblem by half at each level of the recursion but at the same time, the number of subproblems is actually increasing by a lot more! So, the work is dominated by the bottom level of recursion tree. Drawing only the first three levels, you can see, the bottom level will carry most of the work
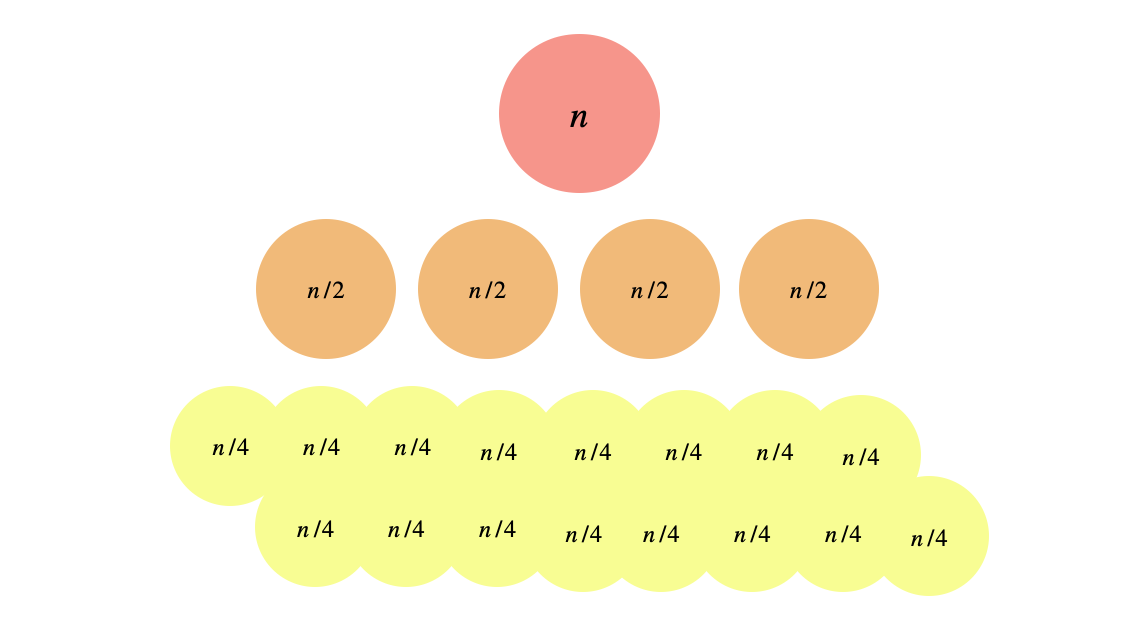 To be precise, we sum all the work done across all levels and use the geometric series \(\sum_{t=0}^{N}x^t = \frac{x^{N+1} - 1}{x - 1}\).
To be precise, we sum all the work done across all levels and use the geometric series \(\sum_{t=0}^{N}x^t = \frac{x^{N+1} - 1}{x - 1}\).
Case 1:
By the master theorem (case 1), the solution should be \(O(\log(n))\). Intuitively, we’re reducing the size of the problem by half at each level of the recursion and at the same time, we’re doubling the number of subproblems (balanced case). So, at each level, we have the same amount of work. If we draw only the first three levels, you’ll notice that at each level, we’re doing precisely \(n\) total amount of work.
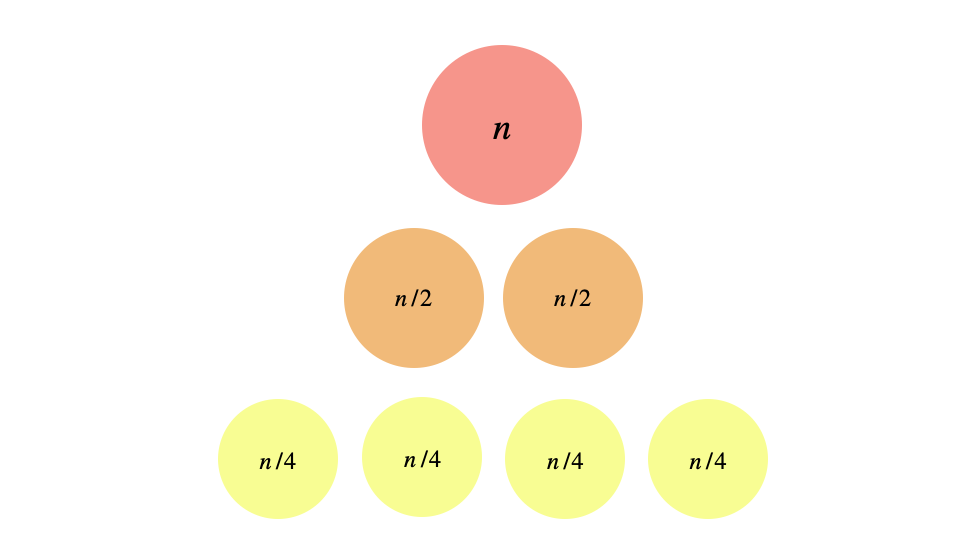 To make this formal, we sum all the work done across all levels,
To make this formal, we sum all the work done across all levels,
Proof Outline
Why is the master theorem correct? Let’s take a look at the recurrence again,
We will assume that \(T(1) = 1\) for simplicity. To solve the recurrence, we will use the recursion tree method similar exactly to what we did for Mergesort. Let’s build the same table that we built for Mergesort to calculate the amount of work done per each level of recursion and get the following,
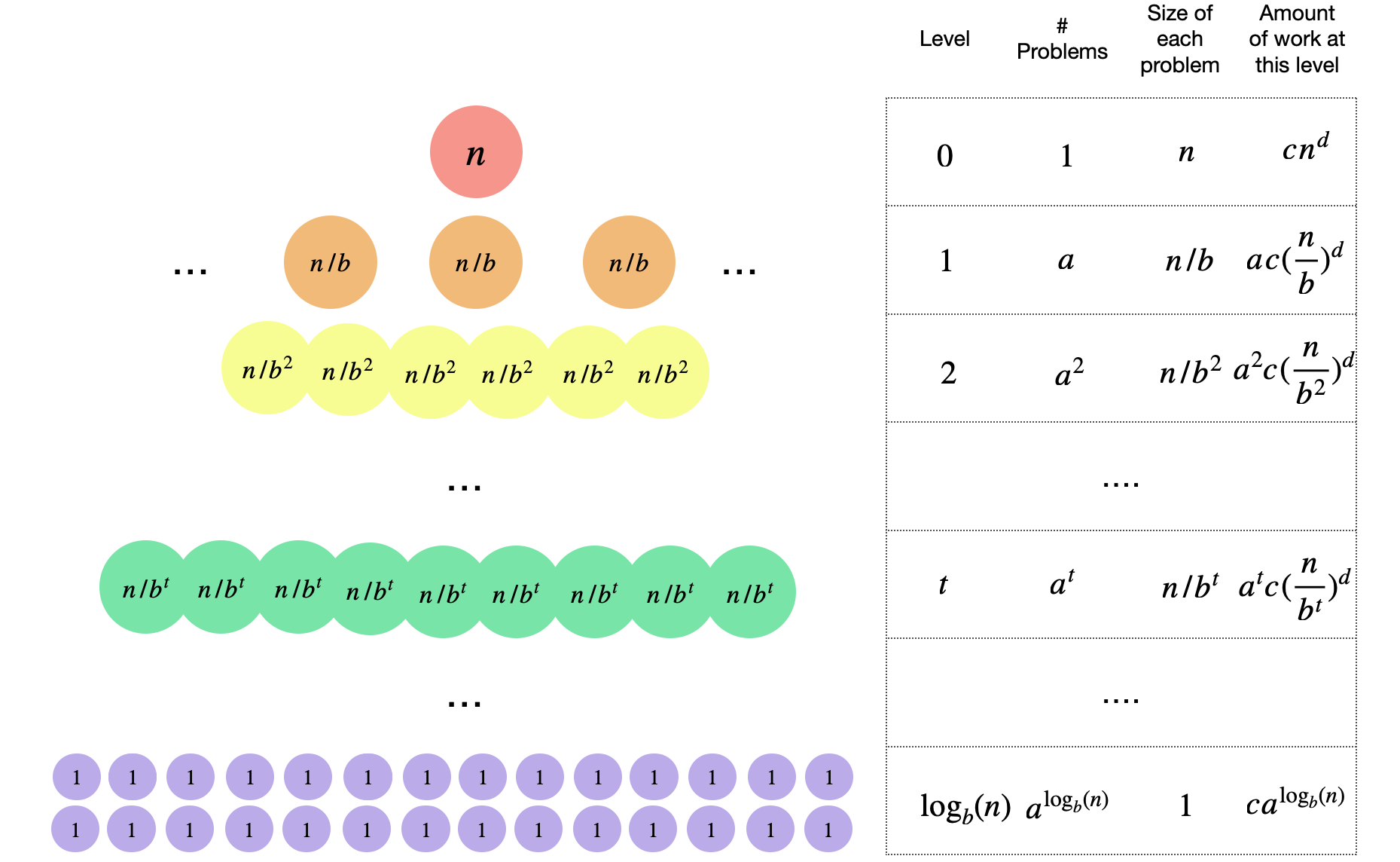
All we need to do now is to sum the amount of work done for all the levels in the table. We see that,
So now we can handle each case.
Case 1: \(a = b^d\)
Case 2: \(a < b^d\)
We note in the above sum that \(\frac{a}{b^d} < 1\). We can then use the geometric series,
When \(|x| < 1\) and the summation is infinite, this sum approaches \(\frac{1}{1-x}\). So, \(\sum_{t=0}^{\log_b(n)} (\frac{a}{b^d})^t\) is bounded by \(\frac{1}{1-a/b^d}\) which is some constant that doesn’t depend on \(n\). Therefore,
Case 3: \(a > b^d\)
We note in the above sum that \(\frac{a}{b^d} > 1\). We can then use the geometric series again,
When \(|x| > 1\) and the summation is infinite, this sum approaches the last term in the series. So, \(\sum_{t=0}^{\log_b(n)} (\frac{a}{b^d})^t\) is bounded by \((a/b^d)^{\log_b(b)}\). Therefore,
References
- Stanford CS161
- CLRS