In this note, we would like to analyze the running time of MergeSort. Recall that MergeSort is a divide and conquer algorithm where we repeatedly split the input into two halfs and then call MergeSort again on each half. Once we’re done, we can combine the halfs in Merge. The follow pesudo-code shows this (Based on CLRS)
MergeSort(A, first, last) {
if (first < last) {
mid = floor((first+last)/2)
MergeSort(A,first,mid)
MergeSort(A,mid+1,last)
Merge(A,first,mid,last)
}
}
Recursion Tree Method
How long does MergeSort take? How many operations are we performing? Let’s look at what MergeSort is doing at each level of of the recursion tree. We will first go all way down splitting the array and calling MergeSort on each half until we reach the base case. And then we will go all way up calling Merge in every level until the final Merge call which combines the two sorted halfs of the array.
Level 0:
At the top level, we have the whole input, array \(A\) of size \(n\). We will recursively call MergeSort on each half of the \(A\).
 Level 1:
Level 1:
In this level, we have two calls to MergeSort. Each call is on one half of the array. The total number of elements from all calls though is still \(n\).
 Level 2:
Level 2:
In level 2, we will have 4 calls. Each call is on an array of size \(n/4\). We also notice here that the total number of elements is also \(n/4+n/4+n/4+n/4=n\).
 Level \(t\):
Level \(t\):
At the \(t\)‘th level, we will have \(2^t\) calls to MergeSort. Each of the arrays passed to MergeSort is of size \(n/2^t\). Again, the total number of elements is also \(n\).
 Level ?:
Level ?:
When do we stop dividing/recursively calling MergeSort? Our base case happens when \(first == last\). This means that we stop the recursion when each call has an array of size 1. How many times do we divide \(n\) by 2 (we’re dividing the array into two halfs at each step) to reach 1? This is precisely what logs give us. \(log_d(n)\) is the number of times that we divide \(n\) by \(d\) to reach 1. Therefore, at the \(log_2(n)\) level, each array will be of size 1 1 and this is when stop calling MergeSort again. After this step, we will start calling Merge now to combine everything together!

Now let’s climb up the recursion tree. Merge merges two sorted arrays with \(cn\) operations where \(n\) is the size of the array and \(c\) is a positive constant. To see why it’s linear, below is what merge is exactly doing
void merge(int a[], int first, int last, int mid) {
int b[mid - first + 1], c[last - mid], i, j;
// fill both arrays with the two sorted halfs
for (i = 0; i < mid - first + 1; i++) { b[i] = a[i + first]; }
for (j = 0; j < last - mid; j++) { c[j] = a[j + mid + 1]; }
int k = 0, m = 0, index = first;
// combine both arrays one element at a time
while (k < i && m < j) {
if (b[k] < c[m]) {
a[index++] = b[k++];
} else {
a[index++] = c[m++];
}
}
while (k < i) { a[index++] = b[k++]; }
while (m < j) { a[index++] = c[m++]; }
}
Level \(log(n):\)
 We know that each array is of size 1 and so there is nothing to do here besides just returning from MergeSort. (Refer to the pseudocode and note (if first < last)). So at this level, we precisely doing \(n\) operations.
We know that each array is of size 1 and so there is nothing to do here besides just returning from MergeSort. (Refer to the pseudocode and note (if first < last)). So at this level, we precisely doing \(n\) operations.
Level \(t\):
 At the \(t\)‘th level, we have \(2^t\) arrays. Each of these arrays is of size \(n/2^t\). We will perform \(n/2^t * c\) operations per call. Summing everything, we have \(2^t * n/2^t * c = cn\) operations.
At the \(t\)‘th level, we have \(2^t\) arrays. Each of these arrays is of size \(n/2^t\). We will perform \(n/2^t * c\) operations per call. Summing everything, we have \(2^t * n/2^t * c = cn\) operations.
So at each level we’re doing at most \(cn\) operations.
Summary
Let’s now summarize everything in a nice table:
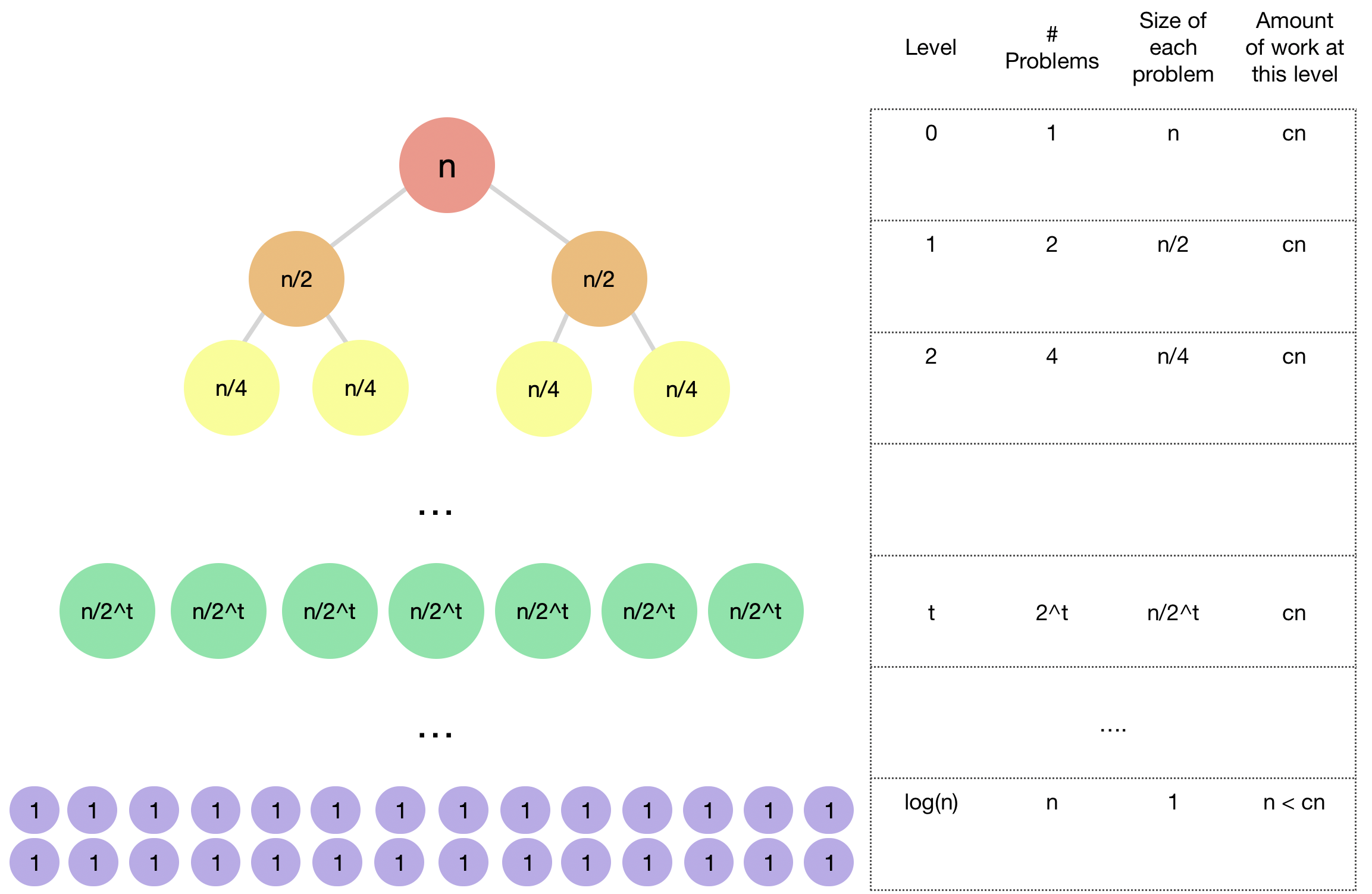
What about the total number of operations for all levels? In other words, what is the running time of merge sort? We have \(log(n)+1\) total levels and in each level we’re doing \(cn\) operations, therefore MergeSort performs \(cn(\log(n)+1)\) operations.
Let \(f(n) = cn(\log(n)+1)\) and \(g(n) = n\log(n)\). To see that \(f(n) = O(g(n))\), recall that we need to find \(c'\) and \(n_0 > 0\) such that for all \(n \geq n_0\), we have \(0 \leq f(n) \leq c'g(n)\)
Choose \(c'=2c\) and \(n_0=2\) and so for all \(n \geq n_0\) and \(c' = 2c\) we need to prove:
Solving for \(n\) (\(n\) is positive)
This is certainly true for all \(n \geq 2\) and so we are done.
The Substitution Method
TODO
References
- Stanford CS161
- CLRS