Let \(G = (V, E)\) be a directed acyclic graph consisting of \(V\) vertices and \(E\) edges. Topological sort is an ordering of the vertices of the graph such that for any given vertices \(u, v \in V\), if \((u,v) \in E\), then \(u\) must come before \(v\) in the ordering. We have already developed an algorithm for topological sort using depth first search here. In this article, we will explore another topological sort algorithm, Kahn’s algorithm.
Kahn's Algorithm
Kahn’s algorithm is extremely intuitive. What are we trying to achieve with topological sort? If we have two vertices/tasks \(u\) and \(v\) where task \(u\) is a perquisite or required to be done before task \(v\), then we want to output \(u\) before \(v\). This dependency is represented with an edge \((u,v)\).
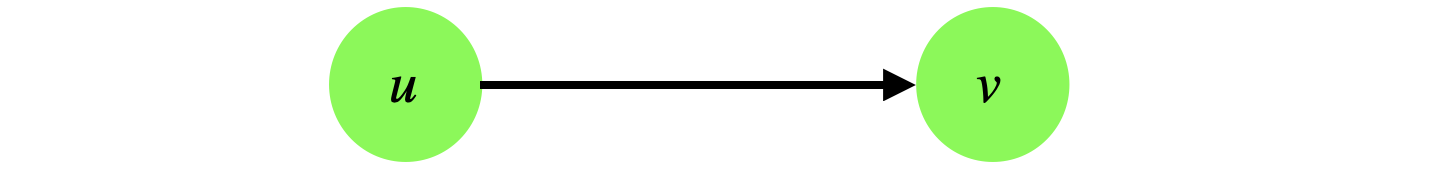
The in-degree of a vertex
This edge contributes to the in-degree of vertex \(v\) and out-degree of vertex \(u\). The in-degree of a vertex is the number of incoming edges into the vertex. The out-degree of a vertex is the number of edges leaving the vertex. In Kahn’s algorithm, we’re interested in the in-degree of each vertex. In the above example, \(v\) has an in-degree of 1.
How does Kahn utilizes the in-degree of a vertex?
Intuitively, if we have a vertex with in-degree \(=0\), then we know that this vertex has no incoming edges. This means that this vertex (task) can be processed/started because it has no dependencies. Therefore, we can just output or add this vertex to the sorted output! This is the whole idea of Kahn’s algorithm.
What if we don’t have a vertex with in-degree 0?
Since the graph is a DAG (no cycles), then it must have at least one node with in-degree \(=0\).
What happens when we don’t have any more vertices with in-degree \(=0\)?
 When we add a vertex to the sorted output, we need to decrement the in-degree count of all its neighbors. In the example above, once we add \(u\) to the sorted output, we need to decrement the in-degree of \(v\). This will lead to \(v\) having an in-degree 0. At this point, we need to also add \(v\) to the sorted output and decrement its neighbors.
When we add a vertex to the sorted output, we need to decrement the in-degree count of all its neighbors. In the example above, once we add \(u\) to the sorted output, we need to decrement the in-degree of \(v\). This will lead to \(v\) having an in-degree 0. At this point, we need to also add \(v\) to the sorted output and decrement its neighbors.
How do we do the above?
We maintain a queue to hold the nodes with in-degree 0 that haven’t been added to the sorted output yet. Every time we pop a vertex from this queue, we do two things:
- Add this node to the sorted output.
- Go through its neighbors, decrement their indegree and push any neighbor with in-degree 0 to the queue.
What if the graph has a cycle?
 If the graph has a cycle, then we will have a situation where multiple vertices won’t reach an indegree of zero ever. That’s totally fine. We only need to check that the sorted output at the end has the same number of vertices in the graph. If that’s not the case, then we know the graph has a cycle and we just return an error.
If the graph has a cycle, then we will have a situation where multiple vertices won’t reach an indegree of zero ever. That’s totally fine. We only need to check that the sorted output at the end has the same number of vertices in the graph. If that’s not the case, then we know the graph has a cycle and we just return an error.
Example
Let’s go through a full example of running Kahn’s algorithm based on the description we gave above. (TODO)
Correctness Proof
How do we prove that Kahn’s algorithm actually returns a correctly sorted vertices? (TODO)
Implementation
void kahn(std::vector<std::vector<int>> &g) {
std::vector<int> in_degree(g.size(), 0);
std::queue<int> q;
// compute the in-degree of each vertex in O(E+V)
for (int u = 0; u < g.size(); u++) {
for (int i = 0; i < g[u].size(); i++) {
int neighbor = g[u][i];
in_degree[neighbor]++;
}
}
// push the vertices of in-degree 0
// if this is a DAG, then we must have some vertex with in-degree=0
for (int u = 0; u < g.size(); u++) {
if (in_degree[u] == 0) {
q.push(u);
}
}
std::vector<int> ordered_vertices;
while (!q.empty()) {
int u = q.front(); // some vertex with in-degree = 0
q.pop();
ordered_vertices.push_back(u);
// decrease the in-degree of all neighbors
for (int i = 0; i < g[u].size(); i++) {
int neighbor = g[u][i];
in_degree[neighbor]--;
// push a vertex with no more dependencies on the queue
if (in_degree[neighbor] == 0) {
q.push(neighbor);
}
}
}
// cycle check
if (ordered_vertices.size() != g.size()) {
printf("cycle!!!!!\n");
return;
}
// print or return ordered_vertices
}Running Time
We compute the in-degree of all vertices in time \(O(E+V)\). The while loop runs in time \(O(E+V)\) since we push and pop a vertex with indegree-0 once. We also loop through the edges of that vertex only once. The total complexity remains at \(O(E+V)\).
References
geeks-for-geeks