Let \(G = (V, E)\) be a directed acyclic graph consisting of \(V\) vertices and \(E\) edges. Topological sort is an ordering of the vertices of the graph such that for any given vertices \(u \in V\) and \(v \in V\), if \((u,v) \in E\), then \(u\) must come before \(v\) in the ordering. For example, we might have some dependency graph of classes and their prerequisites and we want to find an ordering of the classes such that if class \(a\) is a prerequisite to class \(b\), then \(a\) comes before \(b\) in the sorted list.
Revisiting Depth First Search
Believe or not, topological sort is just a depth first search with a minor tweak! In depth first search, we start by visiting some node and marking its start time. We then visit its children and run depth first search again on the children and their descendants. Only after we’re done processing all the neighbors, we mark the node’s finishing time. This means that once we mark a node finished, then it’s impossible for this node to have unvisited neighbors and so this means that all the descendants of this node will have a lower finish time than the node itself! (we’ll prove this). Therefore, we can utilize this idea by pushing the nodes whenever we’re done processing them onto a stack. When there are no longer unvisited nodes, we will end up with the sorted vertices as required.
int dfs(int v, int current_time,
std::vector<std::vector<int>>& graph,
std::vector<std::pair<int,int>> ×,
std::vector<int> &visited) {
times[v].first = current_time++; // mark the start time for v
visited[0] = true;
for (int i = 0; i < graph[v].size(); i++) {
int u = graph[v][i];
if (visited[u] == false) {
current_time = dfs(u, current_time, graph, times, visited);
current_time++;
}
}
times[v].second = current_time; // mark the finish time for v
// we can push the nodes here onto a stack!!! yay
return current_time;
}
Example
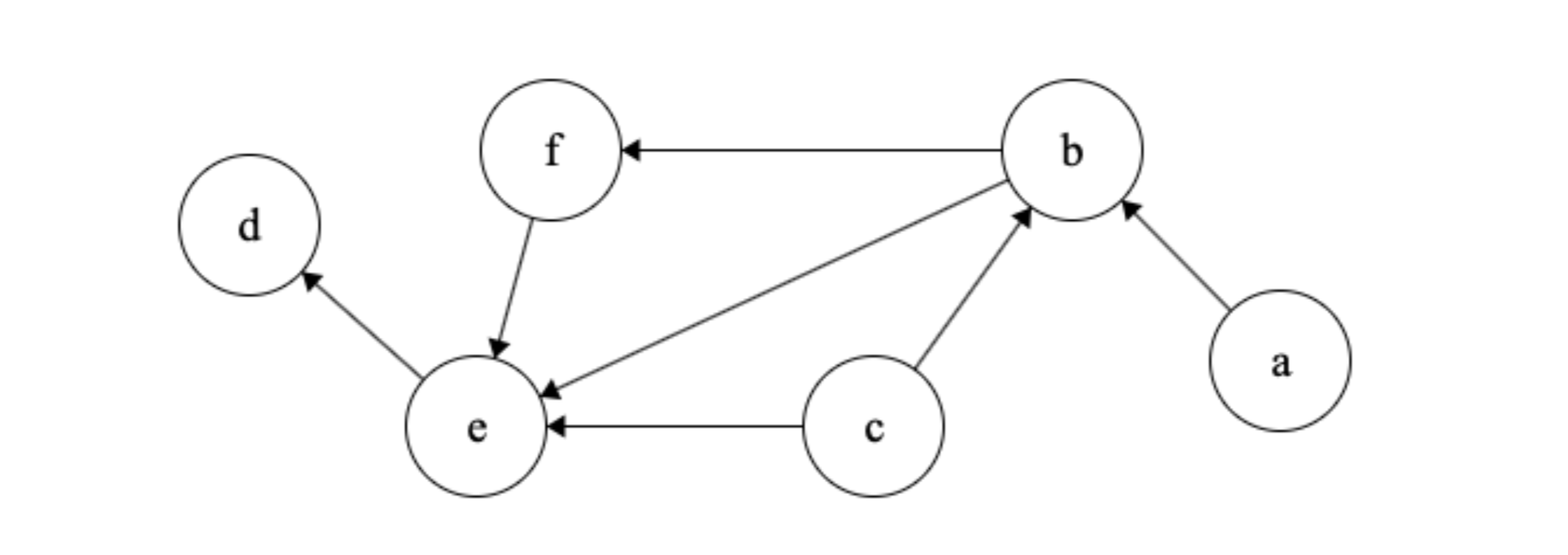 Let’s explore the graph above with dfs to see how the start and finish times are set again. We will start from \(f\) (arbitrarily chosen), mark its start time as zero and visit \(e\). We will mark \(e\)’s start time and then recursively call DFS on \(d\). We will set its start time. At this point, we don’t have more neighbors and so we mark its finish time as well. When we come back, \(e\) won’t have more neighbors and so we will mark its finish time. We do the same thing with \(f\) and we’ll end up with the graph below.
Let’s explore the graph above with dfs to see how the start and finish times are set again. We will start from \(f\) (arbitrarily chosen), mark its start time as zero and visit \(e\). We will mark \(e\)’s start time and then recursively call DFS on \(d\). We will set its start time. At this point, we don’t have more neighbors and so we mark its finish time as well. When we come back, \(e\) won’t have more neighbors and so we will mark its finish time. We do the same thing with \(f\) and we’ll end up with the graph below.
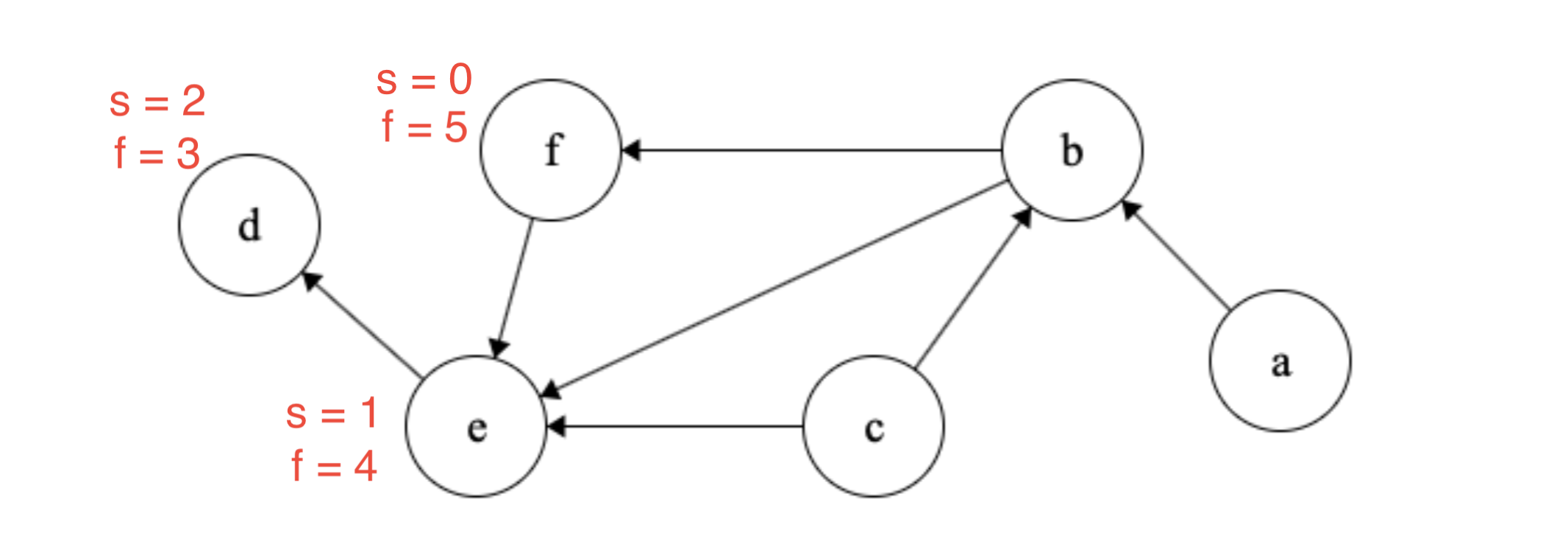
Next we will start from \(c\) and visit \(b\) and mark both their start and finish times. Finally we will visit \(a\) and mark its times as well.
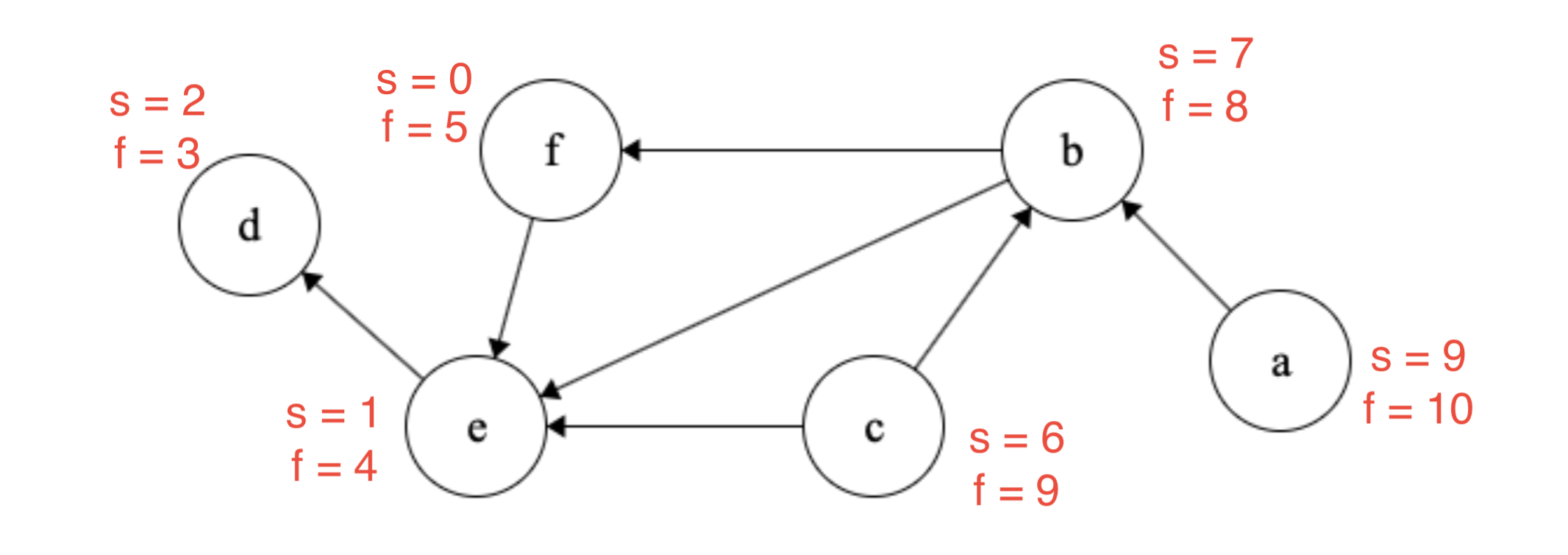
Notice how if we ordered the nodes by their finishing times (\(a, c, b, f, e, d\)) descendingly then we’ll have a valid ordering of the nodes.
Correctness Proof
The first time I saw topological sort I didn’t believe it. It seemed strange to just be able to sort the vertices by just doing a depth first search. What do we need to show to prove that topological sort works? what is the intuition here? Let’s think about this. We need to prove that for any two vertices \(a, b \in V\), if there is an edge from \(a\) to be \(b\), then \(a\) will come before \(b\) in the sorted output.
How do we prove this? Well, we know that topological sort relies on the finishing times of vertices and we know that \(a\)’s finishing time gets marked after its children and so this means that we want to prove that \(a\)’s finishing time is greater than \(b\)’s finishing time. So to summarize, we want to prove the following
claim: For any two vertices \(a, b \in V\), if there is an edge from \(a\) to \(b\), then \(a\)’s finishing time is greater than \(b\)’s finishing time.
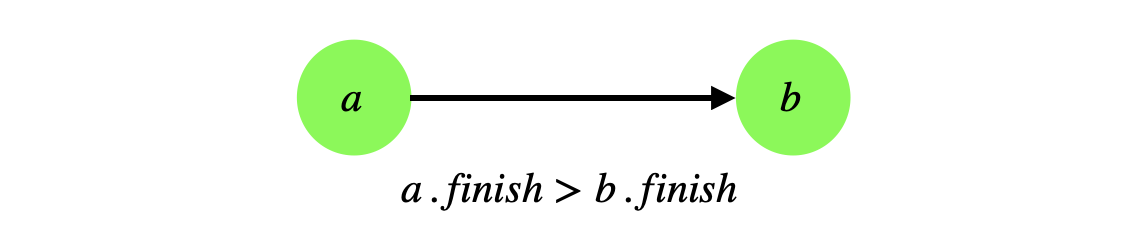
To do so, we will use a theorem called the Parenthesis Theorem from CLRS (proof in CLRS). The parenthesis theorem claims that in a depth first search of a graph \(G = (V,E)\) and for any vertices \(u\) and \(v\), exactly one of the following conditions holds:
-
the intervals [u.start, u.finish] and [v.start, v.finish] are disjoint and neither \(u\) or \(v\) is a descendant of the other in the depth-first forest.
-
the interval [u.start, u.finish] is contained within the interval [v.start, v.finish] and \(u\) is a descendant of \(v\) in the depth-first tree.
-
the interval [v.start, v.finish] is contained within the interval [u.start, u.finish] and \(v\) is a descendant of \(u\) in the depth-first tree.
Proof: TODO!
Now we are ready to prove our earlier claim.
Let \(\)G = (V,E)\(\) be a directed acyclic graph. For any two vertices \(a, b \in V\), if \((a,b) \in E\), then \(a\).finish > \(b\).finish.
Proof:
Let’s consider the depth first tree generated after running depth first search and let’s apply the parenthesis theorem. According to the theorem one of three conditions must hold:
-
the interval [a.start, a.finish] is contained within the interval [b.start, b.finish] and \(a\) is a descendant of \(b\) in the depth-first tree. We claim that this case is impossible because by assumption, we know that \((a,b) \in E\) and so if \(a\) is descendant of \(b\) then \(G\) must have a cycle. This is a contradiction since \(G\) is acyclic.
-
the interval [b.start, b.finish] is contained within the interval [a.start, a.finish] and \(b\) is a descendant of \(a\) in the depth-first tree. This immediately shows that \(b.finish_time < a.finish_time\) as we wanted to show.
-
the intervals [a.start, a.finish] and [b.start, b.finish] are disjoint and neither \(a\) or \(b\) is a descendant of the other in the depth-first forest. In this case, we claim that we must have explored \(b\) first before \(a\). Because if we have explored \(a\) first then we would have explored \(b\) since \((a,b) \in E\) and so we must have \(b.finish < a.finish\) as required. Beautiful isn’t it?
We conclude from all three cases that we must have \(b.finish < a.finish\). \(\blacksquare\)
Implementation
Let’s tweak depth first search to push the nodes onto a stack and let’s forget about the start and finishing times since we only care about returning an ordering of the vertices in this specific case. Let’s call this version topological sort! Here is a simple implementation:
typedef std::vector<std::vector<int>> graph;
void dfs(graph& g, int v, bool *visited, std::stack<int> &ordered) {
visited[v] = true;
for (auto i = 0; i < g[v].size(); i++) {
int u = g[v][i];
if (visited[u] == false) {
visited[u] = true;
dfs(g, u, visited, ordered);
}
}
ordered.push(v); // node is done, we can push it on the ordered stack
}
void topological_sort(graph& g) {
std::stack<int> ordered;
bool visited[MAX] = {false};
// perform dfs until there are no more unvisited nodes
for(int i = 0; i < g.size(); i++) {
if (!visited[i]) {
dfs(g, i, visited, ordered);
}
}
while (!ordered.empty()) {
printf("%s\n", ordered.top());
ordered.pop();
}
}Running Time
It is just DFS! so the total time is \(O(V+E)\).
References
Stanford CS161 Stanford CS161