We previously discussed binary search trees and how the binary search tree property allows us to do tree operations such as insert and delete in just $O(h)$ time. However, if the tree height is of order $O(n)$, then we end up with a worse data structure than just a linked list or a sorted array. What we need is a guarantee that the height is $O(\log(n))$. How can we achieve this?

A red-black tree is a binary search tree that is balanced. By only adding one extra bit to store the color of the node (red or black) and some restrictions on how to insert and delete nodes, we can have a balanced binary search tree that guarantees the height to be $O(\log(n))$.

Red-black tree specifications

A red-black tree must satisfy the following properties:

Every node is either red or black.
The root is black.
Every leaf node is black.
If a node is red, then its children are black.
The number of black nodes must be the same across all simple paths from any node to a leaf node.

Why are red-black trees balanced?

Why do the above properties guarantee anything about the tree being balanced? Intuitively, just restricting the number of black nodes to be the same across all simple paths means that we will have a balanced tree. The red nodes are there to give us some buffer. We could have extra “red” nodes but not a lot in order to keep the height at $O(\log(n))$.

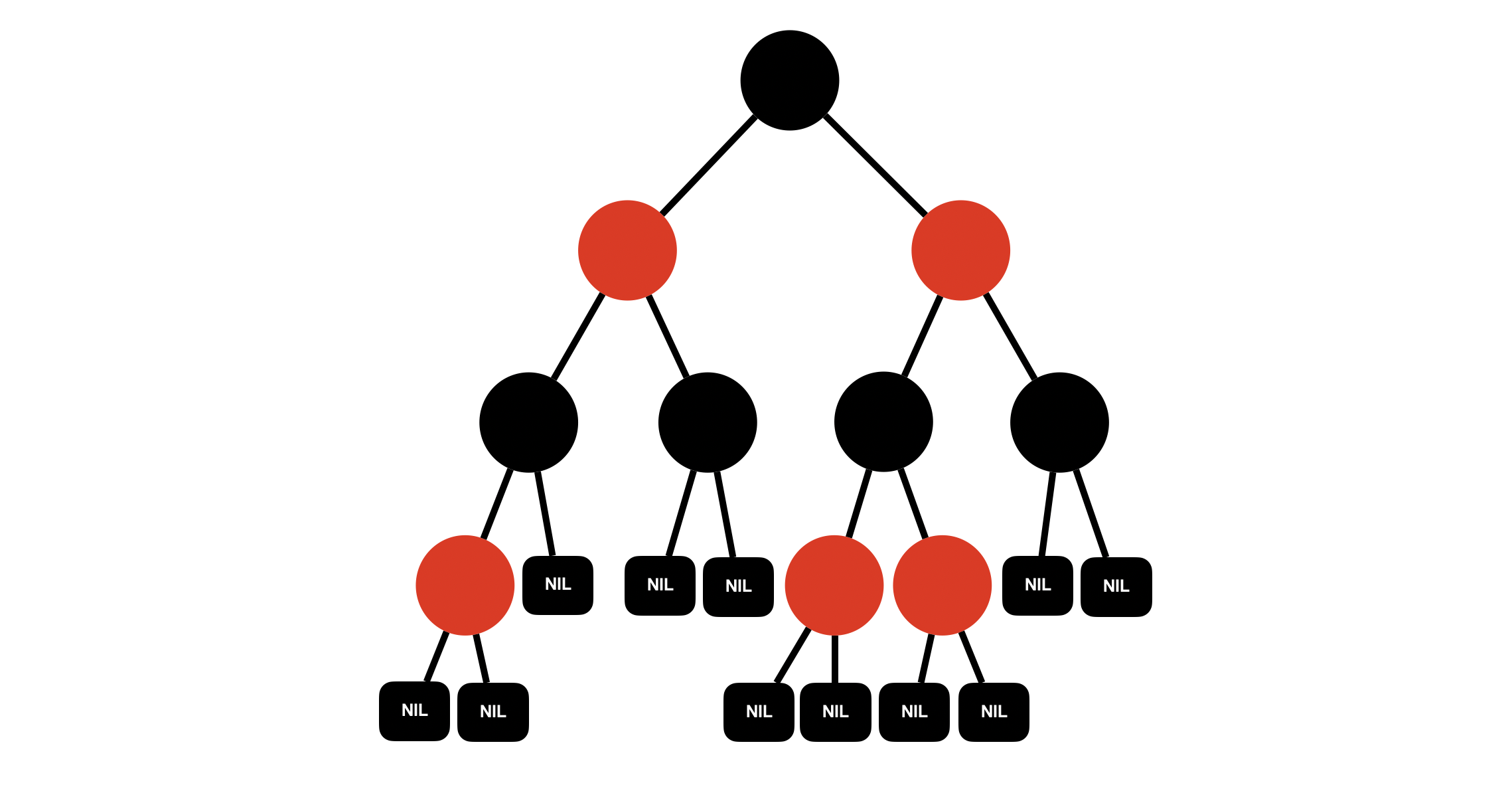
To show a formal proof, we first need to define the black height of a node. Let $bh(x)$ be the black height of a node. $bh(x)$ is number of black nodes from a node $x$ to a leaf but not including $x$ itself. In the above tree, we see that the black height of the root is 2 as every simple path includes exactly 2 black nodes. To show that the height is at most $O(\log(n))$, we want to prove somehow that we have “enough” internal nodes at every node such that the height can’t exceed $O(\log(n))$. Formally, we’ll prove

Given a red-black tree $t$ and a node $x$ in $t$, The subtree rooted at $x$ contains at least $2^{bh(x)}-1$ internal nodes (including x itself)

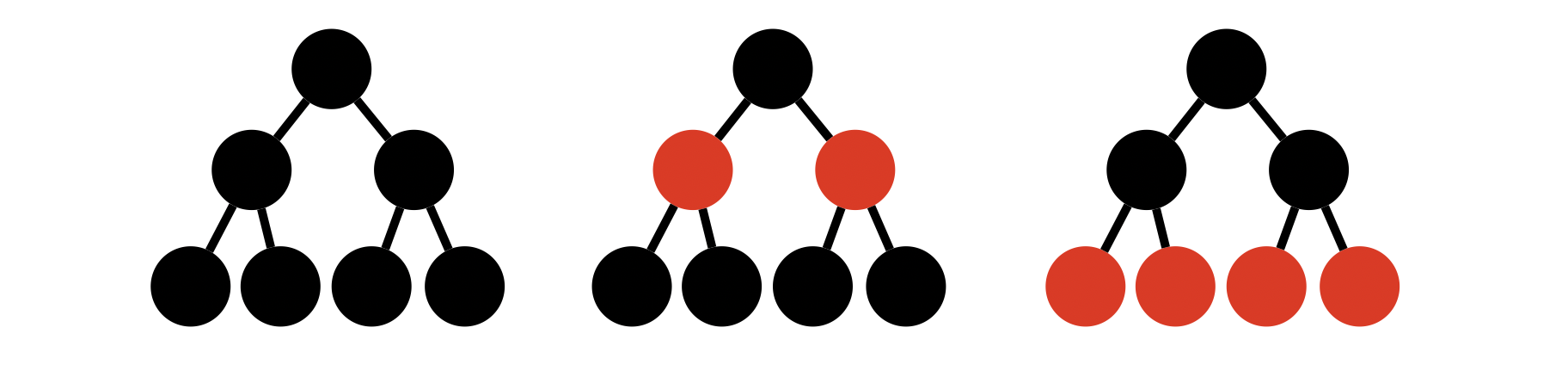
Looking at the figure below, we see in the first figure we have $bh(root)=3$ and we have at least $2^{3}-1=7$ nodes. In the second figure, we have $bh(root)=2$ and at least $2^2-1=3$ internal nodes. Similarly, in the third figure, we have $2^2-1$ internal nodes.

Proof: By Induction on the height of $x$. For the base case, consider when the height is 0, then we know that $x$ is NIL. Therefore, $2^{bh(x)} - 1 = 1 - 1 = 0$. For the inductive step, suppose $x$ has some positive height > 0 and has two internal children (why 2?). Each child must have either $bh(x)-1$ or $bh(x)$ black height depending on its color. If $x$ was red, then both children must be black and the black height of both children is $bh(x)$. If $x$ was black, then both its children must have black height $bh(x)-1$. Since the height of both children is less than $x$, then we can apply the inductive hypothesis and conclude that each child must have at least $2^{bh(x)-1}-1$ internal nodes. Therefore, $x$ has at least $1 + 2^{bh(x)-1} - 1 + 2^{bh(x)-1} - 1 = 2^{bh(x)} -1$ internal nodes which completes the proof. $\blacksquare$

To prove that the height of the tree is at most $O(\log(n))$, . The next thing we want to use is the fact that every red node in a red-black tree must have black children. Therefore, half the nodes on any path must be black. Therefore, if the height of the tree is $h$ then we must have $bh(root) \geq h/2$. Using what we proved earlier, we see that

$$ \begin{align*} n &\geq 2^{bh(root))} - 1 \text{ (using the earlier lemma we proved) }\\ n &\geq 2^{h/2} - 1 \text { (using the fact that red nodes must have black children) }\\ \log(n-1) &\geq h/2 \\ h/2 &\leq \log(n-1) \\ h &\leq 2\log(n-1). \blacksquare \end{align*} $$

Rotations

Operations on red-black trees such as insert and delete modify the tree such that we might violate the red-black tree properties. To restore these properties we perform an essential operation called a rotation. Rotations maintain the binary search property. More on rotations are here.

Insert

Just like inserting a node into a binary search tree, we just find an appropriate place to insert it such that we don’t violate the binary search property. Since all leaf nodes must be black, we create a special dummy node and color it black. We call it SNIL, just to differentiate it from NIL (dumb?).

void Tree::insert(int d) {
    Node *z = new Node(d); // create a new node
    Node *x = root;
    Node *p = SNIL; // potenial parent
    while (x != SNIL) {
        p = x;
        if (z->key < x->key) {
            x = x->left;
        } else {
            x = x->right;
        }
    }
    z->parent = p;
    if (p == SNIL) { // tree was empty
        root = z;
    } else if (z->key < p->key) { // left child
        p->left = z;
    } else {
        p->right = z;
    }
    z->left = SNIL; // new for red-black-trees
    z->right = SNIL; // new for red-black-trees
    z->color = RED; // new for red-black-trees
    insertFixUp(z); // new for red-black-trees
}

Also note that we color the node red by default. Red nodes allow for some room in the definition of a “balanced tree”. We still be okay. If the parent of the node is black, then all is fine. However if we choose to color it black then we immediately violate the property that the number of black nodes must be the same across all simple paths.

In general, there are two main violations that could happen. This could be our very first node which the root and the root must be black. The parent of the node might be red and red nodes are not allowed to have red children.

TODO: EACH CASE :)

Delete

TODO

Implementation

Source Code

References

CLRS