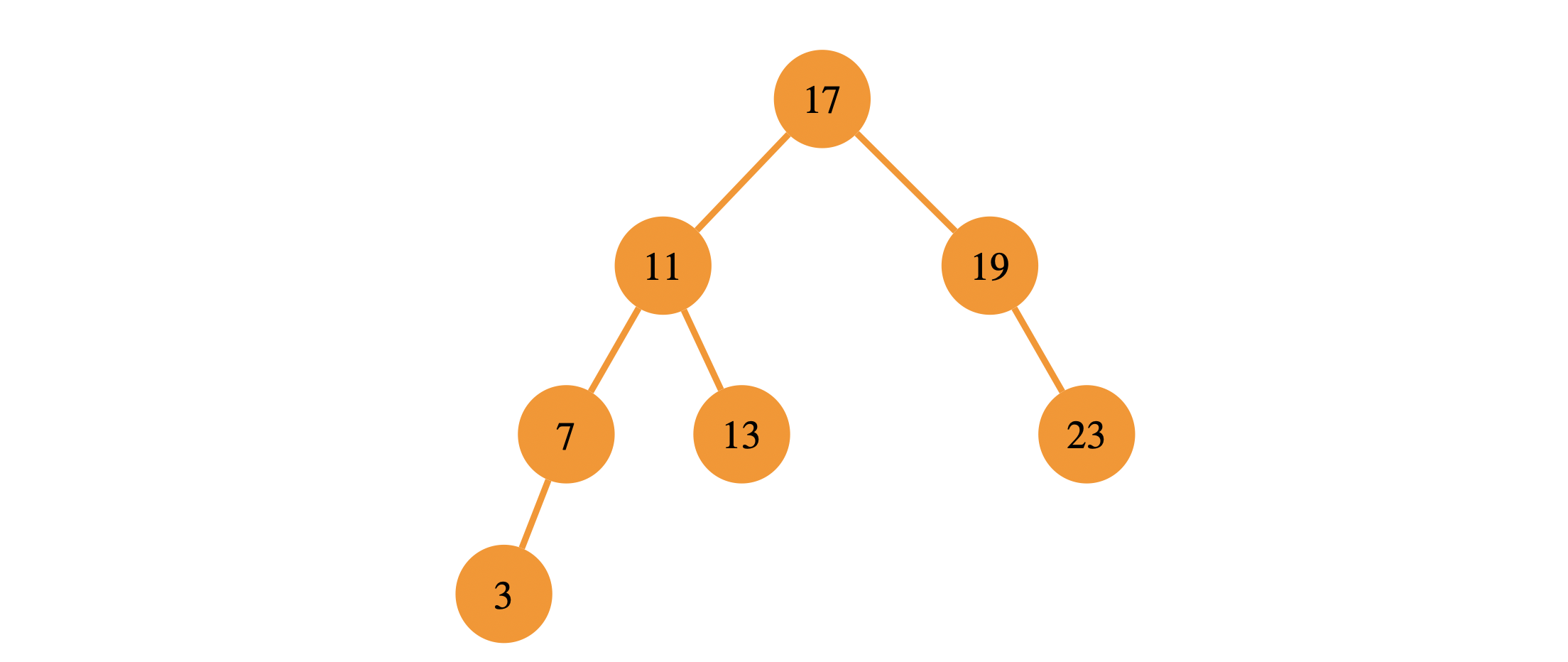
A binary search tree is a binary tree that maintains the binary-search-tree property for every node in the tree. The binary-search-tree property states that given a node \(x\) in the tree, every node in the left subtree has a key less than \(x\)’s key and every node in the right subtree has a key greater than \(x\)’s key.

Motivation

But why invent another data structure? Let’s take a look at sorted arrays. We can search a sorted array for keys in just \(O(\log(n))\) time with binary search. However, inserting and deleting elements takes \(O(n)\) time. Similarly, while inserting elements in a linked list takes only \(O(1)\) time, searching a linked list takes \(O(n)\) time in the worst case. Can we do better with binary search trees? yes!

The binary search tree property is really great at allowing us to insert/search and delete in just \(O(h)\) time since we can eliminate a branch at every single step. Moreover, if the tree is balanced, the height will only be \(O(\log(n))\) where is \(n\) is the number of nodes. Overall, this is a much better data structure for dynamic data than both arrays and linked lists!

In Order Walk

Another great property of binary search trees is that an in order walk of the tree results in getting all the keys sorted. 

void in_order_walk(tree *t) {
    if (t == NULL) { return; }
    in_order_walk(t->left);
    print key
    in_order_walk(t->right);
}

Proving that it takes \(O(n)\) time to perform the in order walk is such a great way to practice the substitution method. (TODO: add proof)

Search

Similar to the in-order walk, we can simply perform a search by using the following 

tree* search(tree *t, key) {
    while (t != NULL && k != t->key) {
        if (key < t->key) {
            t = t->left;
        } else {
            t = t->right;
        }
    }
    return t;
}


Minimum, Maximum, Predecessor and Successor

Similarly, we can find the minimum and maximum by traversing all the way to the left and all the way to the right respectively. For example to find the successor of a node \(x\), we have two cases:

  • If \(x\) has a right subtree, then the most left element (tree minimum) of the right subtree is the successor.
  • If \(x\) doesn’t have a right subtree, then the next element would be the first ancestor such that \(x\) is a left child of it. 
tree* successor(tree *t) {
    if  (t->right != NULL) {
        return tree_minimum(t->right);
    };
    // otherwise, find the closest parent where t is a left child
    tree *p = t->parent;
    while (p != NULL && p->right == t) {
        t = p;
        p = t->parent;
    }
    return p;
}


Insert

Inserting a node into a binary search tree is pretty simple. We need to follow the following steps:

  • Create a new node and assign both the left and right pointers to NULL.
  • Similar to search, descend in the tree with pointer \(current\) based on the key value, while keeping a trailing pointer \(p\) to its parent. Once we hit NULL, we know that the \(p\) will be the parent of our node. The figure below illustrates the process: 
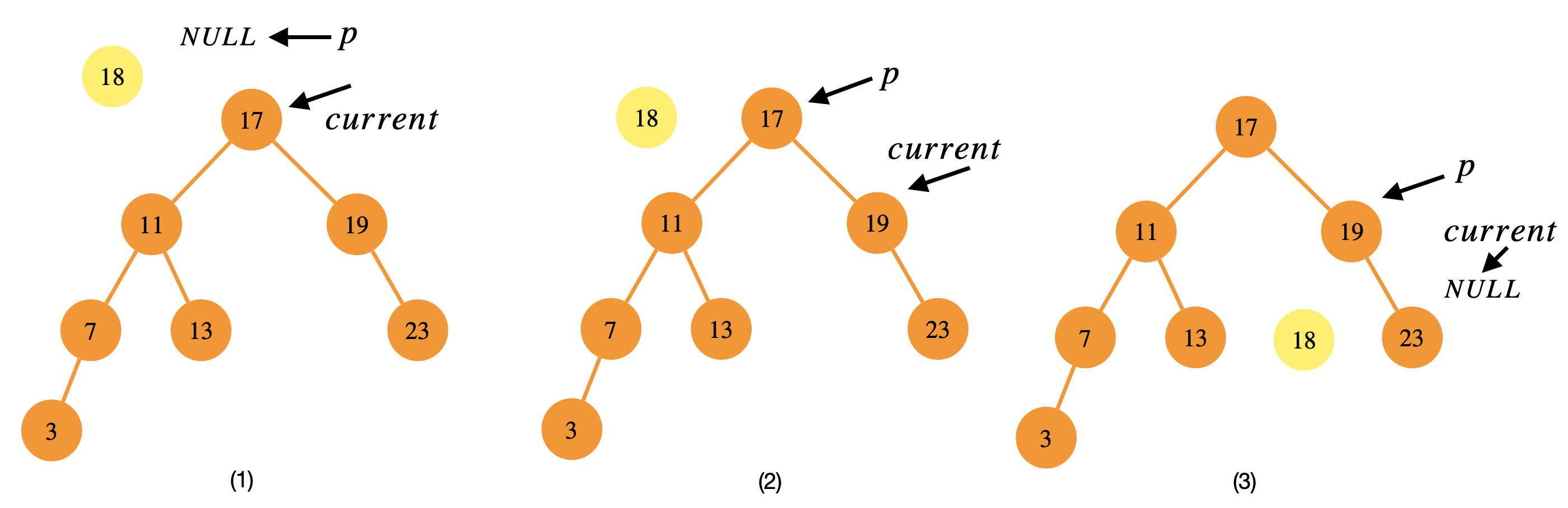
void insert(tree **t, key) {
    // create a new node x
    p = NULL;
    current = *t;
    while (current != NULL) {
        p = current;
        if (x->key < current->key) {
            current = current->left;
        } else {
            current = current->right;
        }
    }
    x.parent = p;
    if (p == NULL) { // x is now the root!
        *t = x;
    } else if (p->key > x->key) {
        p->left = x;
    } else {
        p->right = x;
    }
 }


Delete

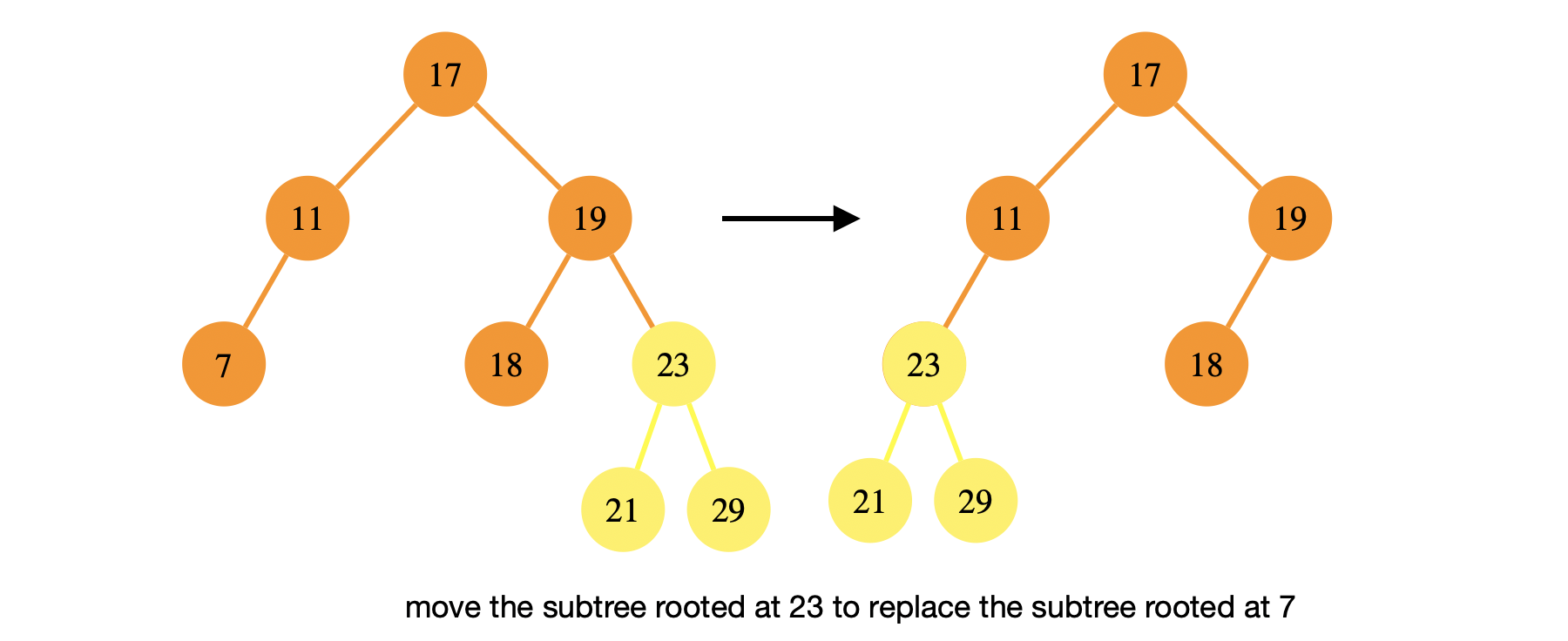
Before discussing delete, we’ll present a helper function that we will use in deleting a node in a binary search three. transplant replaces a subtree rooted at \(x\) with another subtree rooted at \(v\), illustrated below, 

// replace subtree u with subtree v
void transplant(tree **t, tree *u, tree *v) {
    if (u.parent == NULL) { // u is the root 
        *t = v;
    } else if (u == u.parent.left) { // u is a left child
        u.parent.left = v;
    } else if (u == u.parent.right) {
        u.parent.right = v;
    }
    if (v != NULL) { // fix v's parent pointer
        v.parent = u.parent
    }
 }

Now, suppose we’re about to delete node \(x\) and that are given a pointer to it We have four different cases that we need to handle:

  • \(x\) has no children. We then can simply delete that node and return. This case could be handled implicitly in the next case.

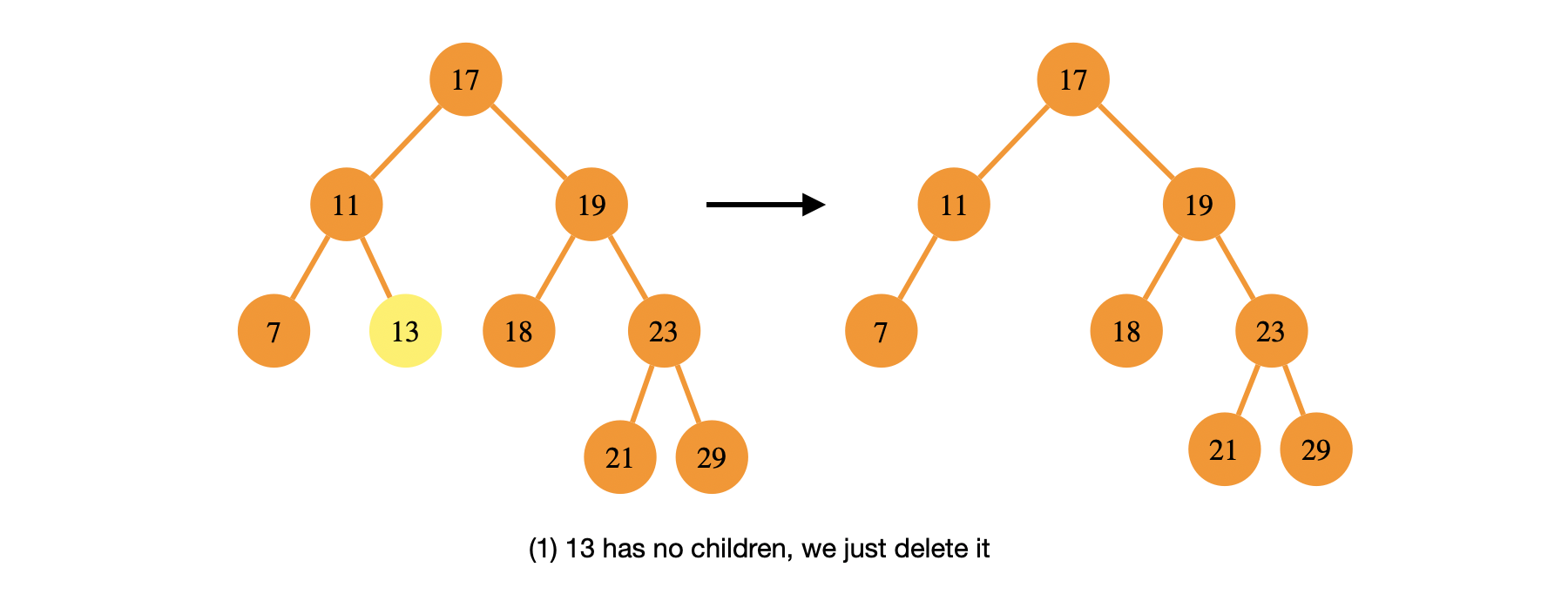
  • \(x\) has only one child. We then just transplant its child at \(x\)’s parent and remove \(x\). 

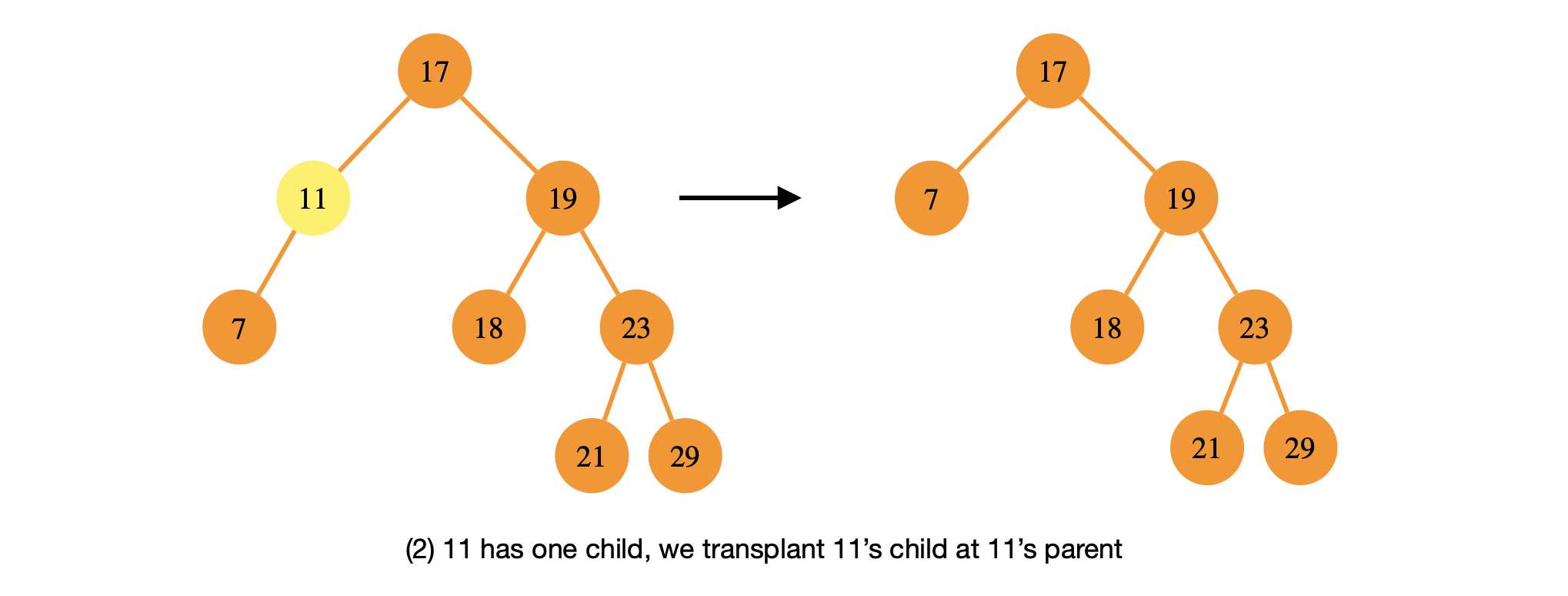
// one child case
// delete node x if x has only one child
if (x.left == NULL) { // no left child
    transplant(*t, x, x.right) // replace x with its right child
} else if (x.right == NULL) { // u is a left child
    transplant(*t, x, x.left) // replace x with its left child
}
// we're good to remove x's memory using "free" or "delete" or whatever we need
  • \(x\) has two children. The idea here is that the successor of \(x\) will take \(x\)’s place to maintain the binary search tree property and then we can just delete \(x\). We do know that the successor is the most left child (minimum node) in \(x\)’s right subtree. Let \(s\) be the successor of \(x\). It is also important to note that \(s\) can’t have left children since it is the most left node by definition. We now break deleting \(x\) into two sub-cases:

(1) \(s\) is the right child of \(x\). In this case, we transplant \(s\) at \(x\)’s parent. We also move \(x\)’s left subtree to be \(s\)’s left subtree. We then we remove \(x\). 

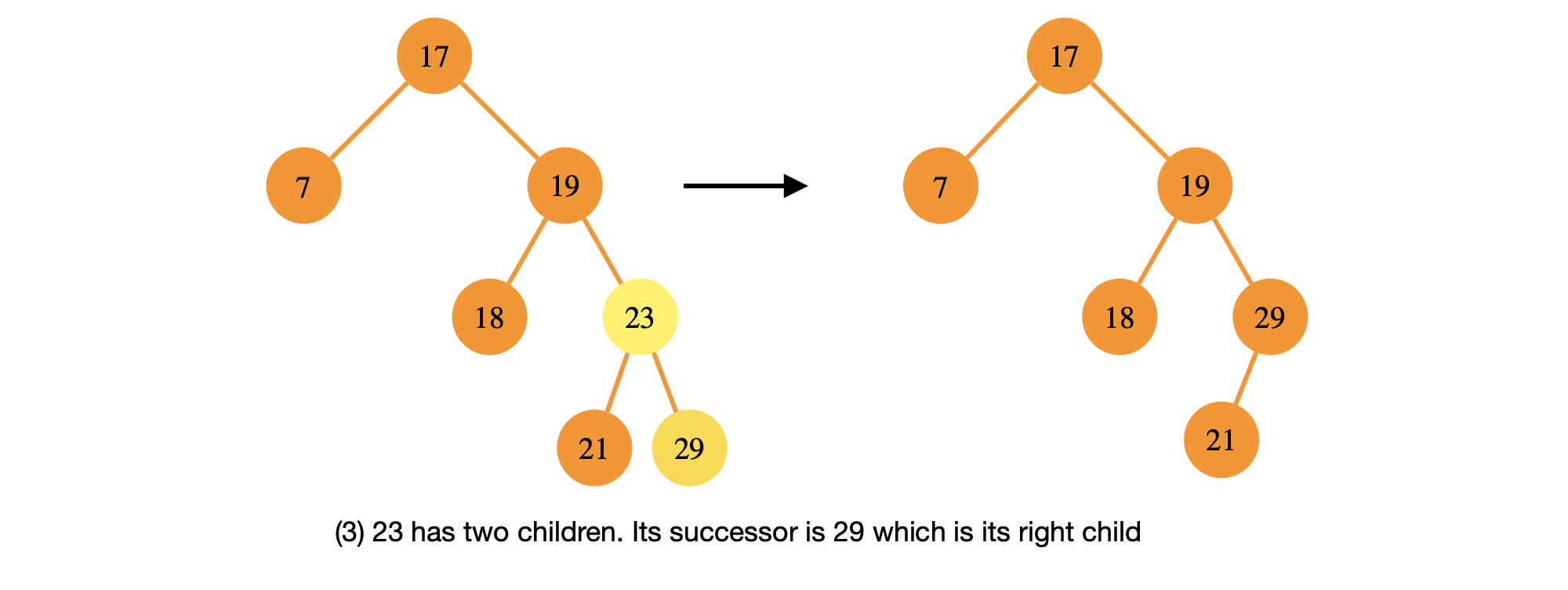
// two children first sub-case (s is a right child of x)
s = minimum(x.right);
if (s->parent == x) { // s is x's immediate right child
    transplant(*t, x, s); // replace x with s
    s->left = x->left; // s's left subtree = x's left subtree
    s->left->parent = s; // we also fix its parent pointer 
}


(2) \(s\) is in the left subtree of \(x\)’s right child. In this case, it’s a little more complicated. We first want to replace \(s\) (21 in the example) with its right subtree (25 in the example) (remember \(s\) can’t have a left subtree). We then assign \(x\)’s right subtree to be \(s\)’s right subtree. So now the subtree 29 is the right child of 21. Finally just like in the earlier case, simply replace \(x\) with its right subtree. In this example, it means to replace 19 with 21! 

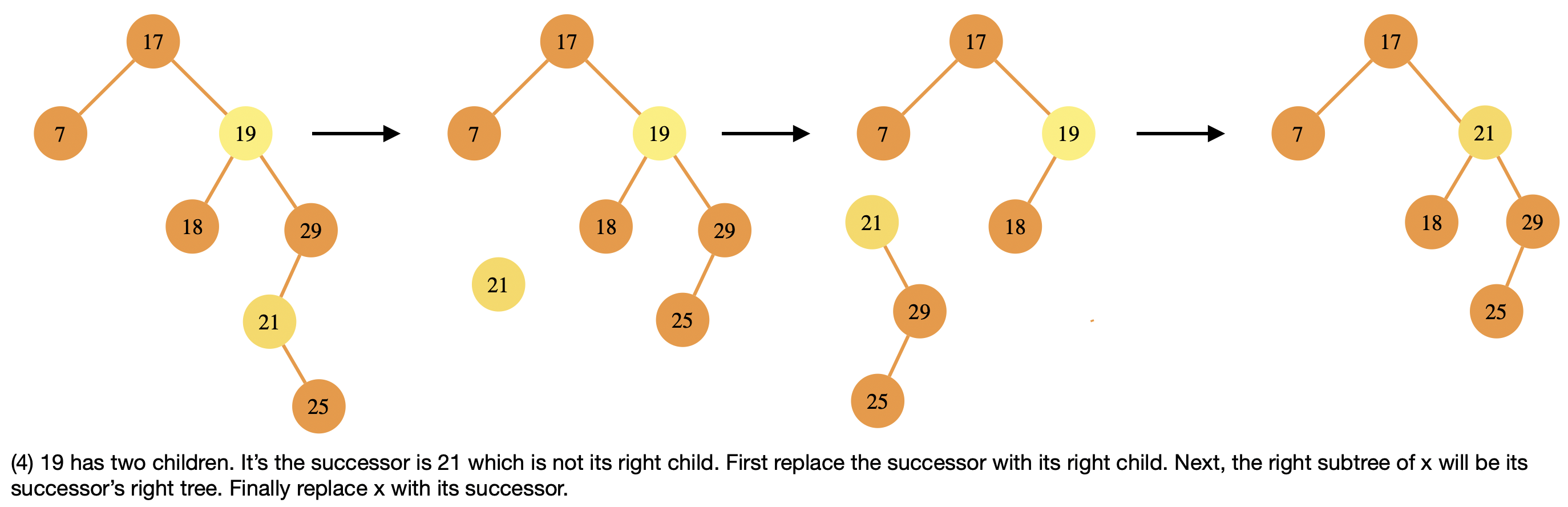
// two children second sub-case (s is not right child of x)
s = minimum(x.right);
if (s->parent != x) { // s is not x's immediate right child
    transplant(*t, s, s.right); // replace s with its right subtree
    s->right = x->right; // s's right subtree = x's right subtree
    s->right->parent = s; // we also fix its parent pointer 
}
// repeat steps from above to replace x with its right child (s)
transplant(*t, x, s); // replace x with s
s->left = x->left; // s's left subtree is now x's left subtree
s->left->parent = s; // we also fix its parent pointer


Finally putting everything together in one place:

void delete(tree **t, tree *x) {
    // one child case
    if (x.left == NULL) { // no left child
        transplant(*t, x, x.right) // replace x with its right child
    } else if (x.right == NULL) { // u is a left child
        transplant(*t, x, x.left) // replace x with its left child
	} else {
    // two children second sub-case (s is not right child of x)
    s = minimum(x.right);
    if (s->parent != x) { // s is not x's immediate right child
        transplant(t, s, s.right); // replace s with its right subtree
        s->right = x->right; // s's right subtree = x's right subtree
        s->right->parent = s; // we also fix its parent pointer 
    }
    transplant(*t, x, s); // replace x with s
    s->left = x->left; // s's left subtree is now x's left subtree
    s->left->parent = s; // we also fix its parent pointer 
}


Implementation

Source Code

References

CLRS