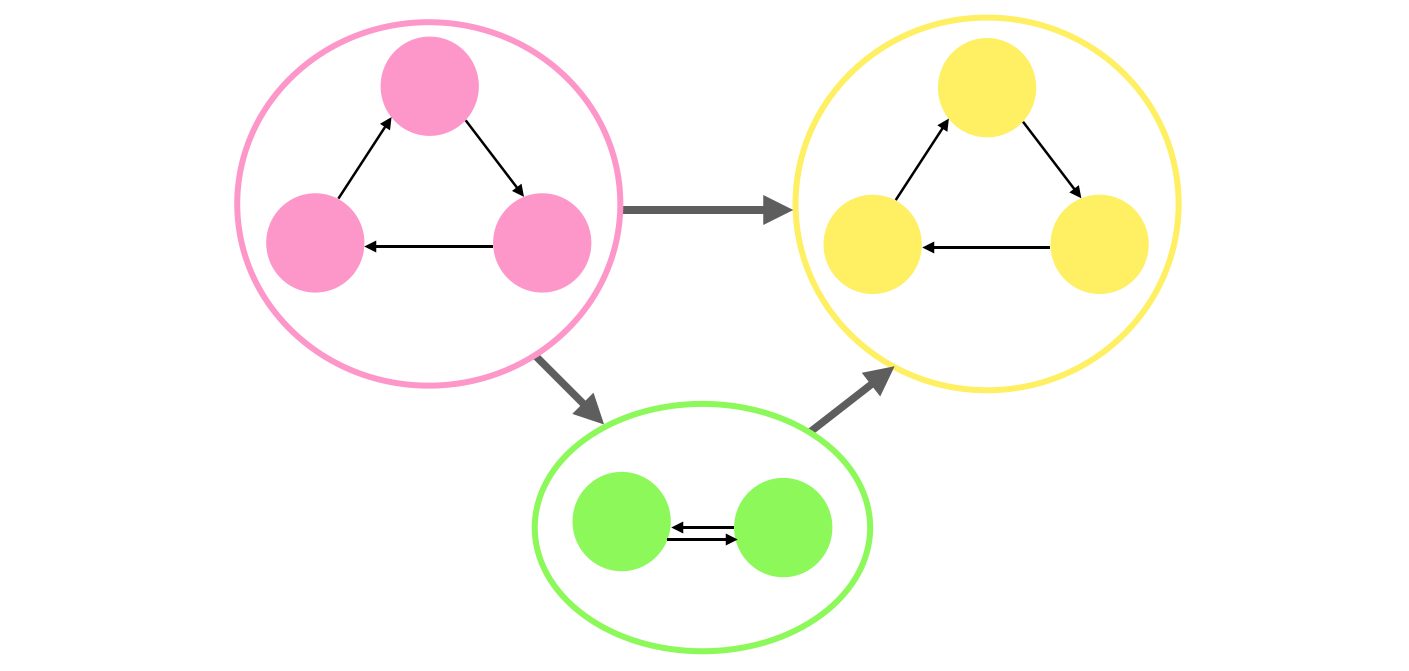
 Let \(G=(V,E)\) be a graph with \(V\) vertices and \(E\) edges. A strongly connected component, \(S\), in \(G\) is a maximal set of vertices \(S \subseteq V\) such that given any two vertices \(u, v \in V\), \(u\) and \(v\) are mutually reachable. In other words, there is a path from \(u\) to \(v\) and a path from \(v\) to \(u\).
Let \(G=(V,E)\) be a graph with \(V\) vertices and \(E\) edges. A strongly connected component, \(S\), in \(G\) is a maximal set of vertices \(S \subseteq V\) such that given any two vertices \(u, v \in V\), \(u\) and \(v\) are mutually reachable. In other words, there is a path from \(u\) to \(v\) and a path from \(v\) to \(u\).
The goal of Kosaraju’s algorithm is to find all the strongly connected components in \(G\).
Algorithm
Kosaraju’s algorithm is shockingly simple. We simply run two passes of depth first search on \(G\). Here is a sketch of what the algorithm is all about,
(1) Run depth first search on G and keep track of finishing times.
(2) Reverse all the edges in G.
(3) Run depth first search on the reversed graph from the node with the largest finishing time.
The connected components in step 3 are the strongly connected components (SCCs))Since all we’re doing is a depth first search, the running time is astonishingly \(O(n+m)\). The following is a full implementation of Kosaraju hosted on Github.
Example
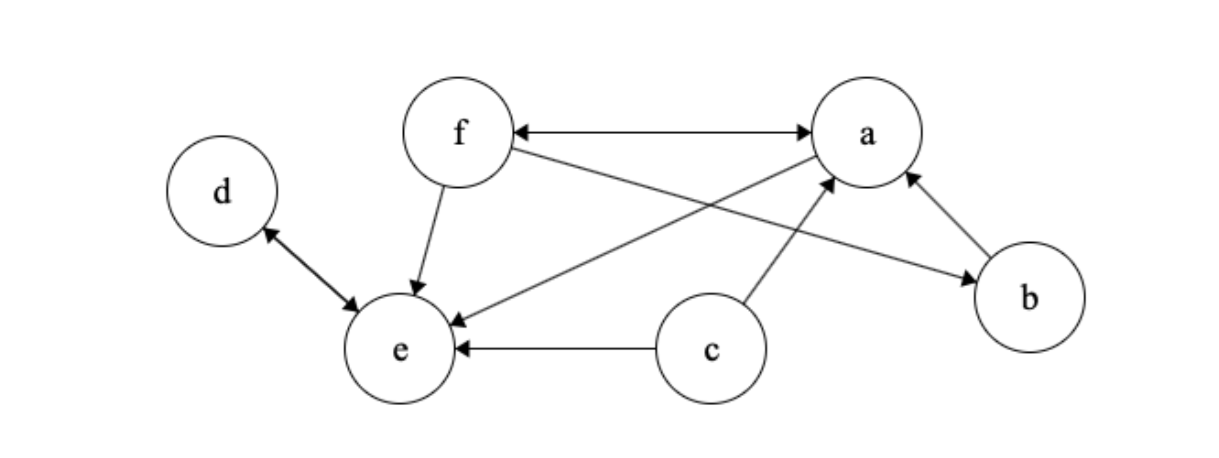 Let’s apply Kosaraju’s algorithm on the graph above. First, we need to run depth first search on the graph while keeping track of the finishing times of vertices. We start by visiting \(a\) and mark the start time as 0. We will continue to visit \(f\) and then \(b\) marking their start times below.
Let’s apply Kosaraju’s algorithm on the graph above. First, we need to run depth first search on the graph while keeping track of the finishing times of vertices. We start by visiting \(a\) and mark the start time as 0. We will continue to visit \(f\) and then \(b\) marking their start times below.
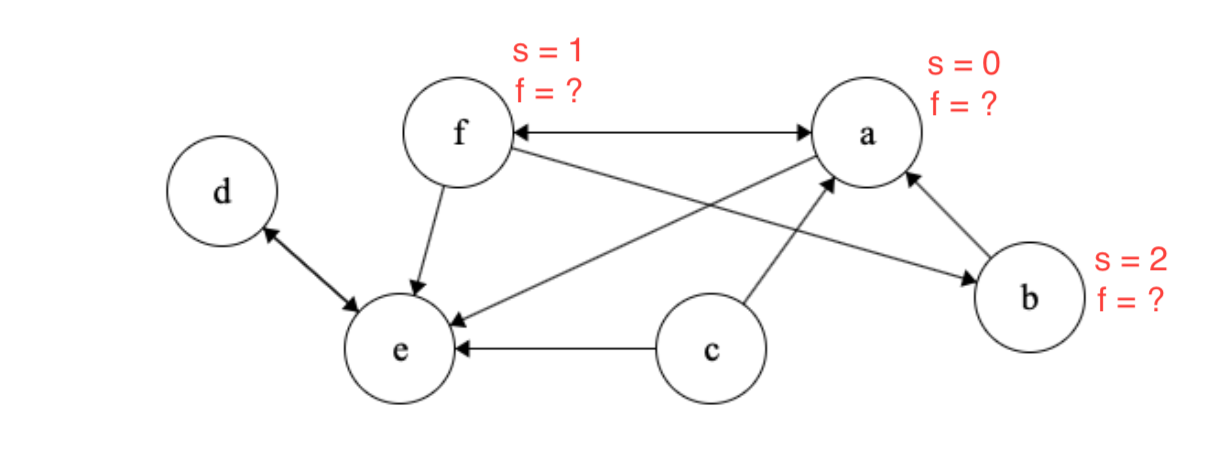 At this point, \(b\) doesn’t have any more neighbors to visit, and so we mark it as finished with finish time = 3. We then go back to \(f\) and visit \(e\) and \(d\) and mark them as finished as they don’t neighbors.
At this point, \(b\) doesn’t have any more neighbors to visit, and so we mark it as finished with finish time = 3. We then go back to \(f\) and visit \(e\) and \(d\) and mark them as finished as they don’t neighbors.
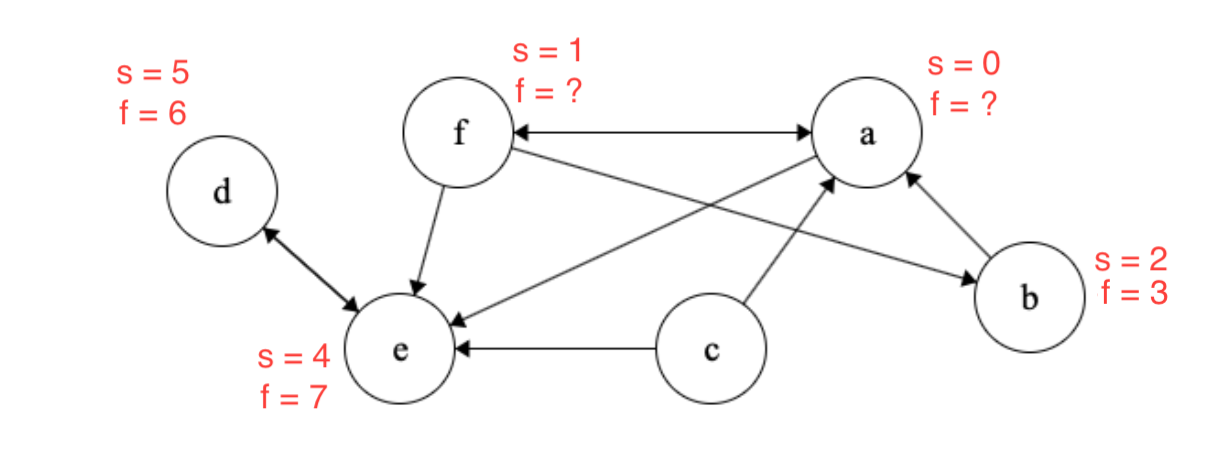 Next, we see that \(f\) doesn’t have any more neighbors and so we mark \(f\) as finished with finishing time = 8. We finally return to \(a\) and mark it as finished as it doesn’t have any more neighbors.
Next, we see that \(f\) doesn’t have any more neighbors and so we mark \(f\) as finished with finishing time = 8. We finally return to \(a\) and mark it as finished as it doesn’t have any more neighbors.
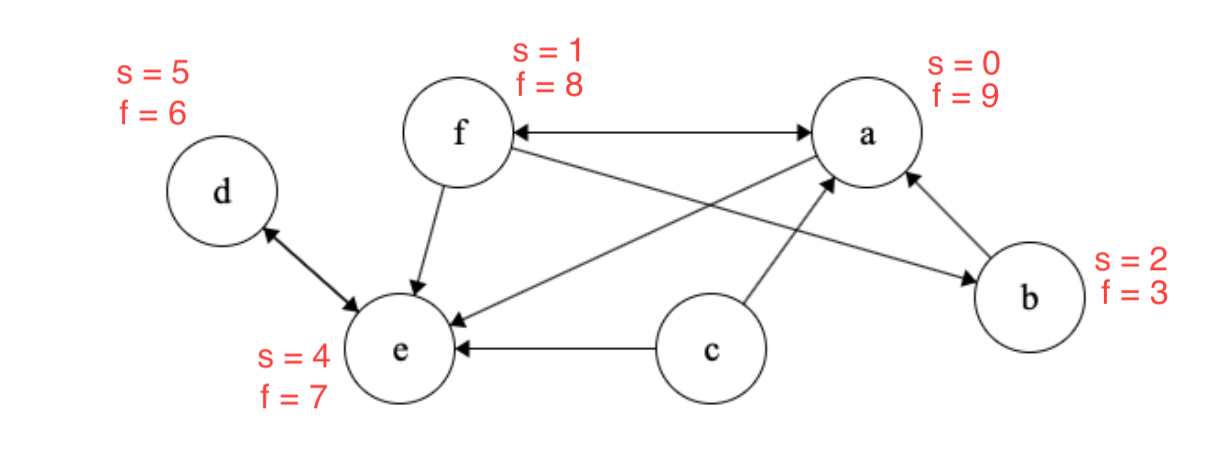 We finally visit \(c\) and mark it as finished. Note that \(c\) has the largest finishing time in \(G\).
We finally visit \(c\) and mark it as finished. Note that \(c\) has the largest finishing time in \(G\).
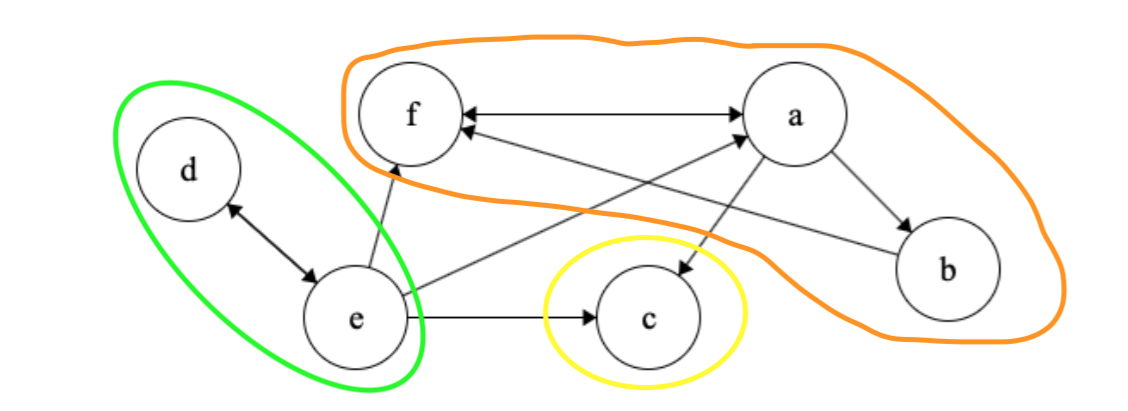
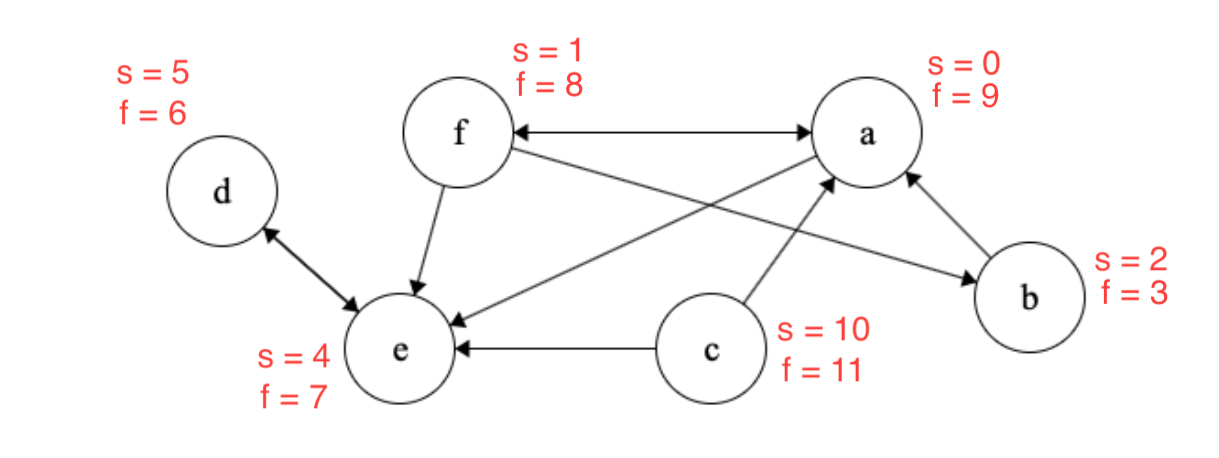 Great! The second step of Kosaraju’s algorithm is to reverse all the edges in \(G\).
Great! The second step of Kosaraju’s algorithm is to reverse all the edges in \(G\).
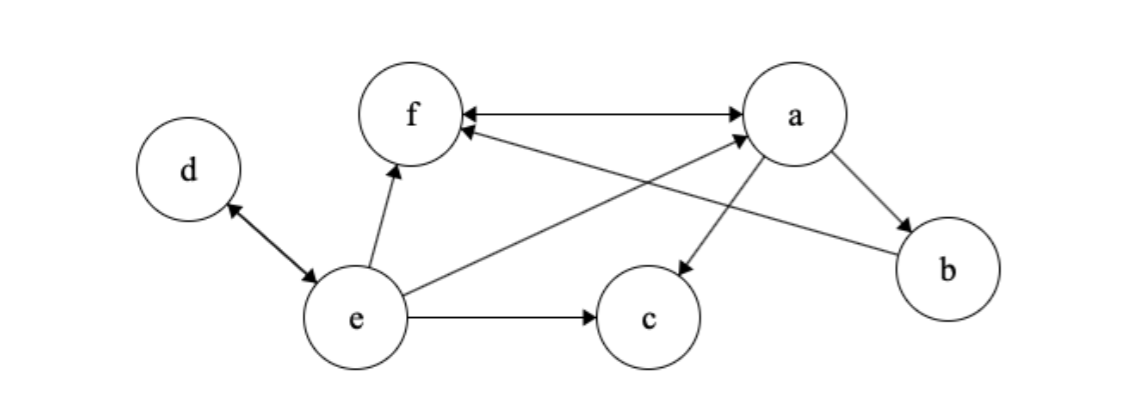 Finally we run another pass of depth first search on the reversed version of \(G\) starting with the node with the largest finishing time from the first pass. We therefore start with \(c\). We notice that \(c\) can’t reach any vertices and so \(c\) is the first strongly connected component in \(G\).
Finally we run another pass of depth first search on the reversed version of \(G\) starting with the node with the largest finishing time from the first pass. We therefore start with \(c\). We notice that \(c\) can’t reach any vertices and so \(c\) is the first strongly connected component in \(G\).
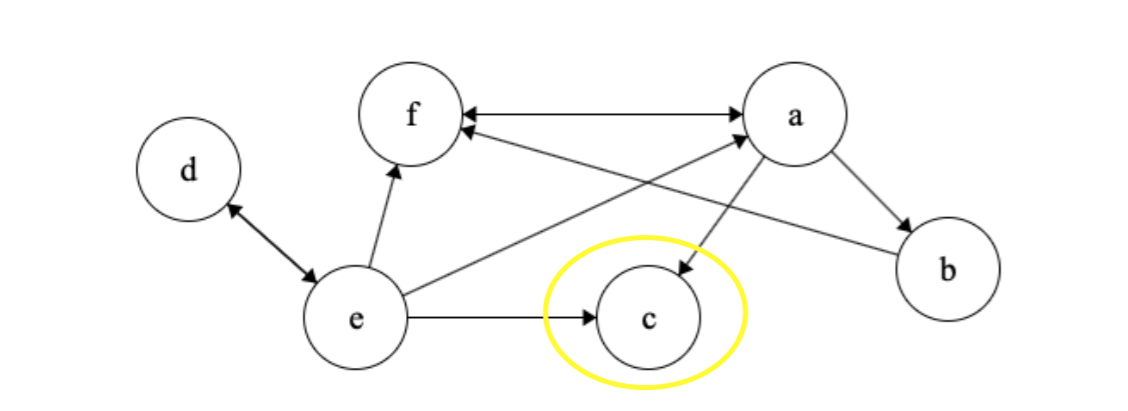 We next visit \(a\), \(f\) and \(b\) and that’s our second strongly connected component.
We next visit \(a\), \(f\) and \(b\) and that’s our second strongly connected component.
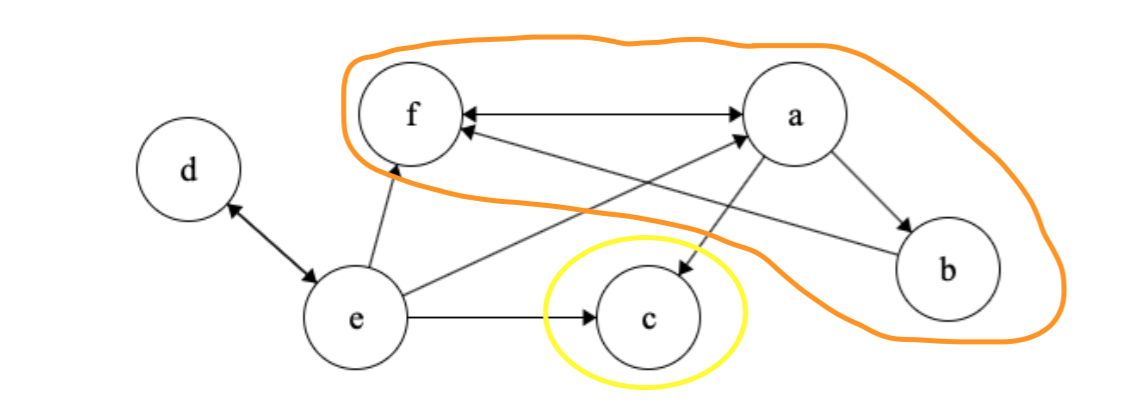 We finally visit \(d\) and \(e\) and that’s our third and final strongly connected component as expected.
We finally visit \(d\) and \(e\) and that’s our third and final strongly connected component as expected.
Correctness Proof
Why does this algorithm find the SCCs? To show why it beautifully works, we’ll breakdown the proof into proving a small claim followed by two lemmas that will be used in the correctness proof.
Claim: Let \(G\) be a graph. Let \(u\) and \(v\) be vertices in \(G\). If \(u\) and \(v\) are mutually reachable and \(v\) and \(w\) are mutually reachable then \(u\) and \(w\) are mutually reachable
Proof: We can construct a path from \(u\) to \(w\) by first going from \(u\) to \(v\) since they are mutually reachable and then going from \(v\) to \(w\) for the same reason. We can construct the reversed path from going from \(w\) to \(v\) since they are mutually reachable and then going from \(v\) to \(u\). Therefore, \(u\) and \(w\) are mutually reachable. \(\blacksquare\)
Lemma 1: The SCC graph is a directed acyclic graph (DAG)
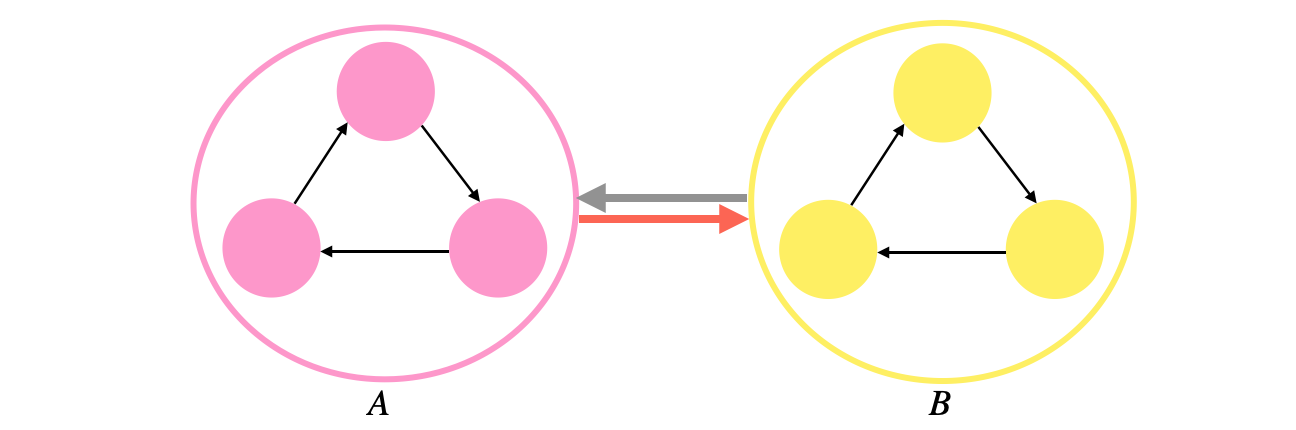 Proof: Suppose that the SCC graph is not a DAG. Therefore, we must have some cycle in the SSC graph. Without the loss of generality, let \(A\) and \(B\) be two components in that cycle. We claim that \(A\) and \(B\) must be in the same connected component and therefore, it is a contradiction to the assumption that the SCC graph is not a DAG.
Proof: Suppose that the SCC graph is not a DAG. Therefore, we must have some cycle in the SSC graph. Without the loss of generality, let \(A\) and \(B\) be two components in that cycle. We claim that \(A\) and \(B\) must be in the same connected component and therefore, it is a contradiction to the assumption that the SCC graph is not a DAG.
Since \(A\) and \(B\) participate in some cycle, then there must be some vertices \(x\) and \(y\) in \(A\) and \(B\) respectively, such that \(x\) and \(y\) are mutually reachable. Since \(A\) is a strongly connected component then \(x\) is mutually reachable from every other vertex in \(A\). Similarly, \(y\) is mutually reachable from every other vertex in \(B\). By the earlier claim, this means that every vertex in \(A\) must be mutually reachable from every other vertex in \(B\). Therefore, the vertices in \(A\) and \(B\) must be in the same strongly connected component and so the SCC graph must be a DAG. \(\blacksquare\)
Before introducing the next lemma, let \(G\) be a graph and let \(A\) be a strongly connected component. We will denote \(A.finish\) as the maximum finish time of all the vertices in \(A\).
Lemma 2: In the SCC DAG, if there is an edge from component \(A\) to component \(B\) then \(A.finish > B.finish\)
Proof: There are two cases:
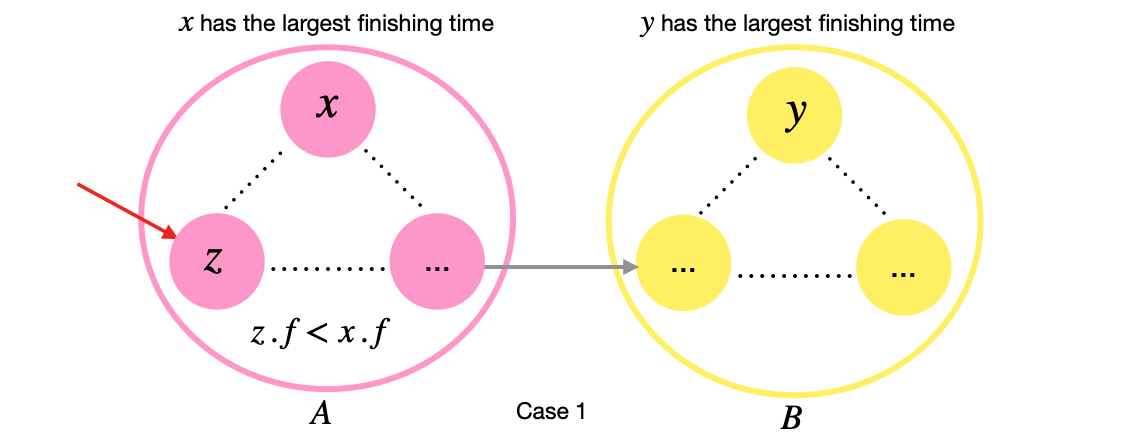 Case 1: We reached \(A\) before \(B\) in our first depth first search pass: Let \(x\) have the largest finishing time in \(A\) and \(y\) have the largest finish time in \(B\). Let \(z\) be the first node discovered in \(A\), then we will reach \(A\) and discover \(z\), then at some point we will reach \(B\) and discover \(y\). This means that \(y\) is a descendant of \(z\). By the parentheses theorem (used in proving topological sort here), this means that \(z\) has a larger finish time. Since \(x\) has the largest finish time in \(A\), then \(x.finish > y.finish\) and since \(y\) has the largest finishing time in \(B\), then we have \(A.finish > B.finish\), as required.
Case 1: We reached \(A\) before \(B\) in our first depth first search pass: Let \(x\) have the largest finishing time in \(A\) and \(y\) have the largest finish time in \(B\). Let \(z\) be the first node discovered in \(A\), then we will reach \(A\) and discover \(z\), then at some point we will reach \(B\) and discover \(y\). This means that \(y\) is a descendant of \(z\). By the parentheses theorem (used in proving topological sort here), this means that \(z\) has a larger finish time. Since \(x\) has the largest finish time in \(A\), then \(x.finish > y.finish\) and since \(y\) has the largest finishing time in \(B\), then we have \(A.finish > B.finish\), as required.
Case 2: We reached \(B\) before \(A\) in our first depth first search: Since we assumed that there is an edge from \(A\) to \(B\) then by Lemma 1, then we must not have an edge from \(B\) to \(A\) (otherwise we’re not a DAG!). Therefore, we will explore \(B\) completely first and then \(A\) will be explored at a later stage. This means that \(A.finish > B.finish\), as we wanted to show. \(\blacksquare\)
Corollary 1: In the SCC DAG, if there is an edge from component \(B\) to component \(A\) in the reversed graph, then \(A.finish > B.finish\)
We can now combine the previous results to prove the following theorem:
Theorem: Kosaraju's algorithm correctly finds the strongly connected components
Proof:
Inductive Hypothesis: The first \(t\) trees found in the second (reversed) DFS
forest are the \(t\) SCCs with the largest finish times. Moreover, what’s left unvisited after these \(t\) trees have been explored is a DAG on the un-found SCCs.
Base Case: It is vacuously true that the first 0 trees found in the reversed DFS forest are the 0 SCCs with the largest finish times. Moreover, what’s left unvisited after 0 trees have been explored is a DAG on all the SCCs by Lemma 1.
Inductive Step: Assume by the inductive hypothesis that the first \(t\) trees are the last-finishing SCCs, and the remaining SCCs form a DAG.
Now, consider the \(t+1\)st tree produced and let \(x\) be the root of the tree. Let \(x\)’s SCC be \(A\). We know that \(A.finish\) must be greater than the finish time of any remaining SSC. This is due to the fact that we chose \(x\) because it was the vertex with the largest finishing time from the remaining vertices. Moreover, we are guaranteed to not have any edges from \(A\) to any remaining SSCs and this is due to Corollary 1. (if there was an edge to some component \(C\), then \(C.finish > A.finish\) which is a contradiction since \(A\) has the largest finish time)
Therefore, we will only discover the vertices in \(A\) from \(x\). So the \(t+1\)st tree is the SCC with the (t+1)st biggest finish time. Also the remaining SCCs still form a DAG, since removing an SSC won’t create a cycle.
Conclusion: The second (reversed) DFS forest contains all the SCCs as its trees. \(\blacksquare\)
Practice Problems
11504 - Dominos (Almost Kosaraju but not quite)
References
- CS161 Stanford
- Algorithm Design