[3.2] Exercise 18
Use conjugation to give a complete bijective proof for the identity $$p(n \mid \leq m\text{ parts}) = p(n \mid \text{all parts }\leq m)$$
Proof
If we start with a partition of \(n\) with at most \(m\) parts, then the corresponding Ferrers graph has at most \(m\) rows. With conjugation, rows becomes columns. Thus, it will have at most \(m\) columns. This means, each row has a maximum length of \(m\) which means that each part is at most \(m\).
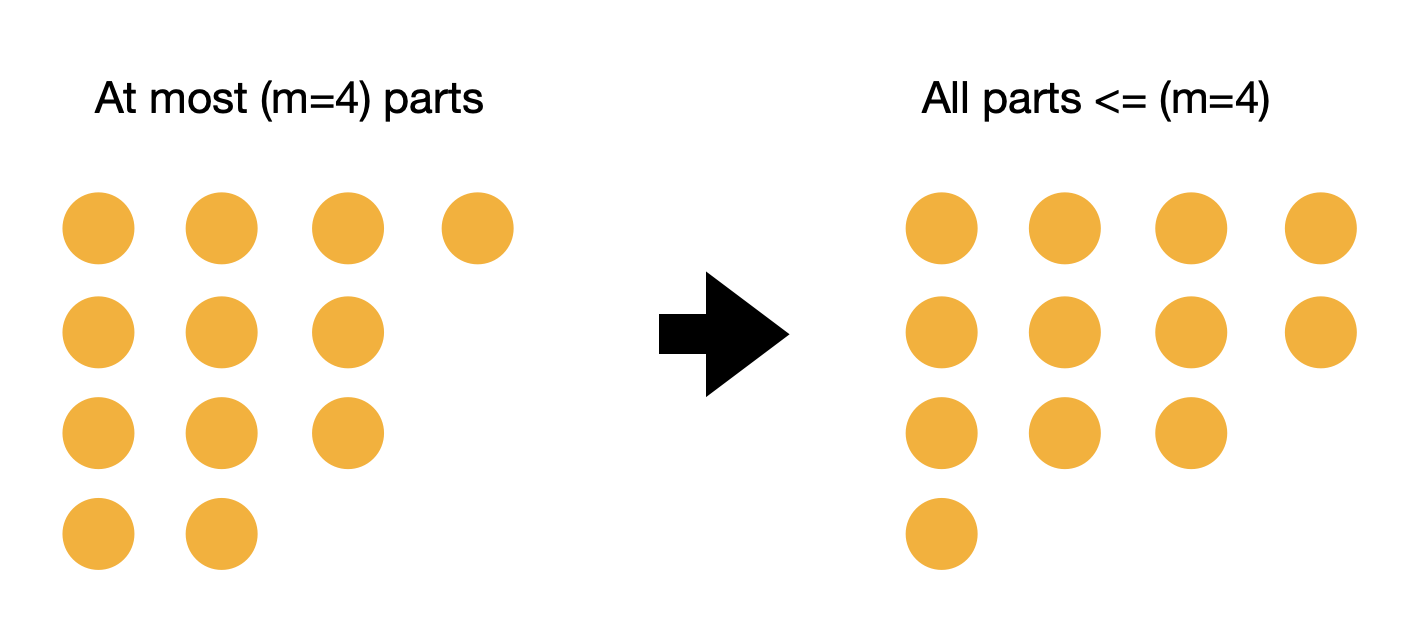
Conversely, conjugation maps partitions whose parts are all at most \(m\) to partitions with at most \(m\) parts.