[3.2] Exercise 17
For \(n=7\) and \(m=3\), explicitly show how conjugation proves Eq. (3.1) by listing all the pairings of partitions.
Proof
We want to show how conjugation proves the identity (3.1) when \(n = 7\) and \(m = 3\):
$$
\begin{align}
p(7 \mid 3\text{ parts}) = p(7 \mid \text{greatest part is } 3)
\end{align}
$$
First, the possible partitions of \(7\) using exactly \(3\) parts is
$$
\begin{align}
7 &= 3 + 3 + 1 \\
7 &= 3 + 2 + 2 \\
7 &= 4 + 2 + 1 \\
7 &= 5 + 1 + 1
\end{align}
$$
We then conjugate each partition above by transforming rows to columns as follows
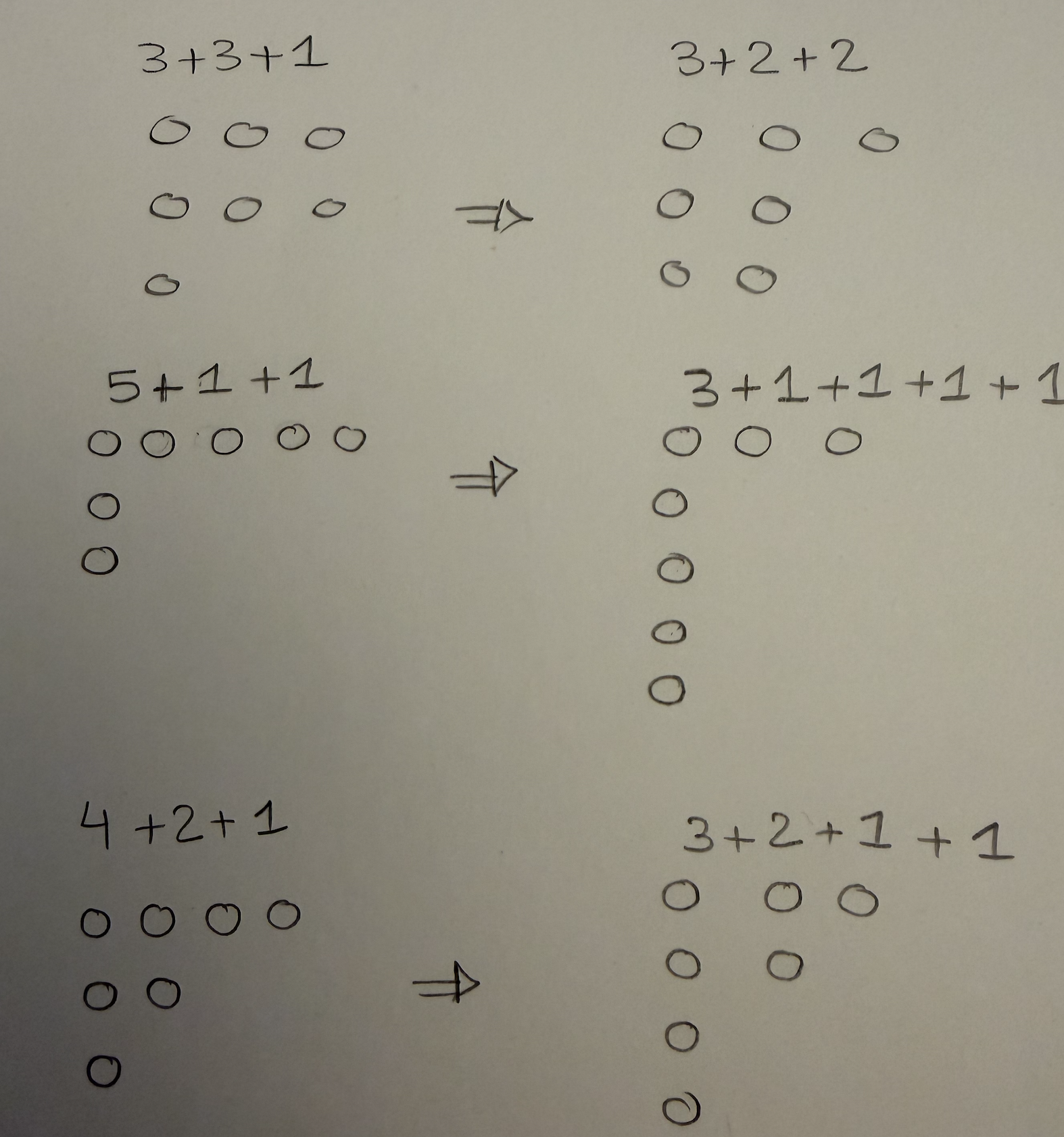
We will get exactly
$$
\begin{align}
7 &= 3 + 3 + 1 \rightarrow 3 + 2 + 2 \\
7 &= 3 + 2 + 2 \rightarrow 3 + 3 + 1 \\
7 &= 4 + 2 + 1 \rightarrow 3 + 2 + 1 + 1 \\
7 &= 5 + 1 + 1 \rightarrow 3 + 1 + 1 + 1 + 1
\end{align}
$$
Note that the greatest part in each of the above partitions is \(3\).