Fixed Point Theorem
Let \(f: [0,1]\to [0,1]\) be a continuous function whose domain and codomain are all \([0,1]\). Show that there always exists \(x_0\) such that $$ f(x_0) = x_0. $$ (\(x_0\) is called the fixed point of \(f\))

Notes

What is this theorem or exercise saying? We’re just looking to show that in the following graph

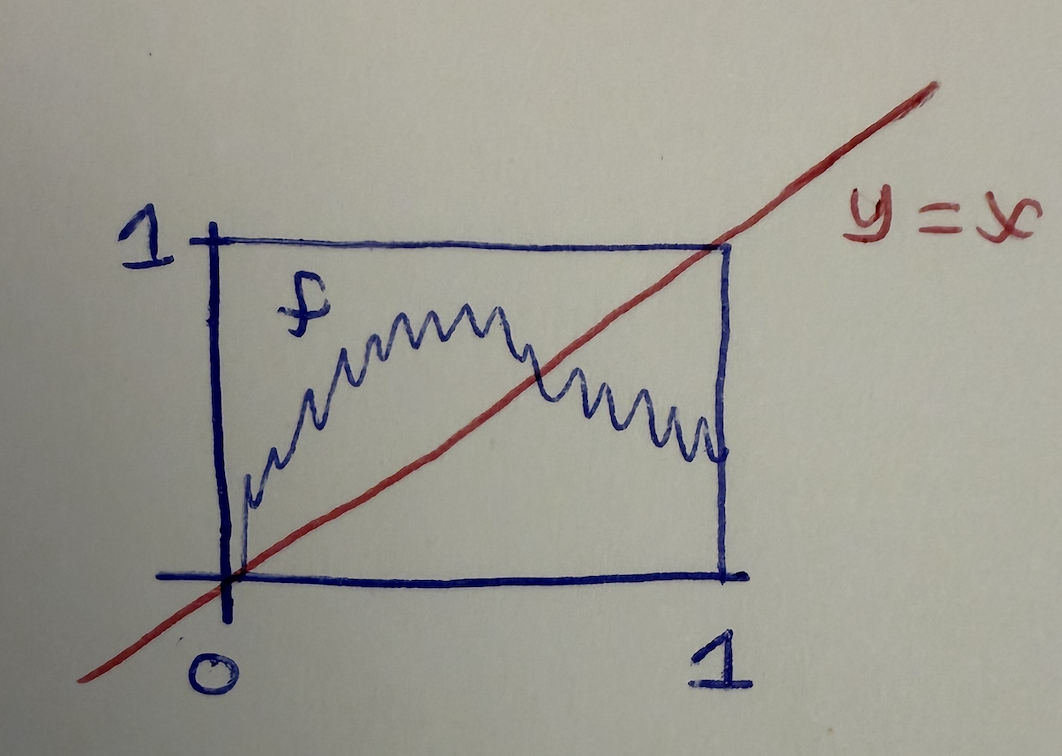
We must hit the diagonal at some point. Since \(f\) is continuous on a closed and bounded interval, then IVT says we can draw the function in a single stroke and every point in the range gets hit. Therefore, we must hit some point on that diagonal. To show this, we do the same thing we did in the IVT proof. Translate the function down so define \(g(x) = f(x)-x\). Then, if \(g(x) > 0\), we’re above the diagonal. If \(g(x) < 0\), we’re below the diagonal and if \(g(x) = 0\), then \(y=x\).

Proof

First note that \(f(0) \geq 0\) and \(f(1) \leq 1\). Now, consider \(g(x) = f(x) - x\). Then

$$ \begin{align} g(0) &= f(0) - 0 \geq 0 \\ g(1) &= f(1) - 1 \leq 0 \end{align} $$

Hence \(0\) lies between \(g(0)\) and \(g(1)\). Since \(g(0) \geq 0\) and \(g(1) \leq 0\). The intermediate value theorem says that there exists some point \(x_0 \in (0,1)\) such that

$$ \begin{align} g(x_0) = 0 \end{align} $$

This means that

$$ \begin{align} f(x_0) - x_0 &= 0 \\ f(x_0) &= x_0. \ \blacksquare \end{align} $$

References