Definition (5.1)
Let \(a,b \in \mathbb{R}\) with \(a < b\). Then
  1. A partition of the interval \([a,b]\) is a set of points \(P = \{x_0,x_1,...,x_n\}\) such that $$a = x_0 < x_1 < \ldots < x_n = b$$
  2. The norm of a partition \(P = \{x_0,x_1,...,x_n\}\) is the number $$\lVert P \rVert = \max_{1 \leq j \leq n} |x_j - x_{j-1}|$$
  3. A refinement of a partition \(P = \{x_0,x_1,...,x_n\}\) is a partition \(Q\) of \([a,b]\) which satisfies \(Q \supseteq P\). In this case, we say that \(Q\) is finer than \(P\).

So the norm of the partition is the length of the biggest sub-interval if we imagine that the interval is cut into all these subintervals \(x_i, x_{i+1}\). For example in

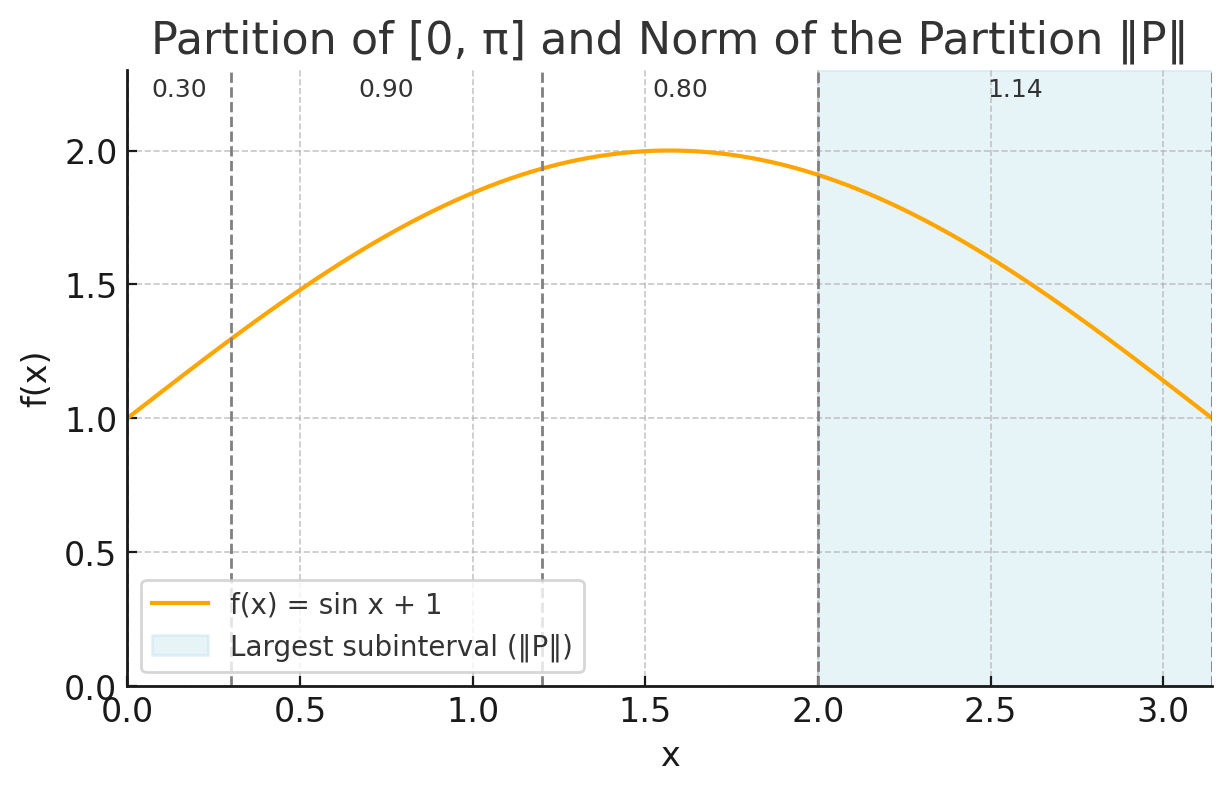
we see that the norm is the interval highlighted in blue since it’s the largest interval.

Definition (5.3)
Let \(a,b \in \mathbb{R}\) with \(a < b\). Let \(P = \{x_0,x_1,...,x_n\}\) be a partition of the interval \([a,b]\), set \(\Delta x_j = x_j - x_{j-1}\) for \(j = 1,2,\ldots,n\) and suppose that \(f:[a,b] \rightarrow \mathbb{R}\) is bounded.
  1. The Upper Riemann Sum of \(f\) over \(P\) is the number $$U(f,P) := \sum_{j = 1}^{n} M_j(f) \Delta x_j$$ where $$M_j(f) := \sup f([x_{j-1}, x_j]) := \sup_{t \in [x_{j-1}, x_j]} f(t) $$
  2. The Lower Riemann Sum of \(f\) over \(P\) is the number $$L(f,P) := \sum_{j = 1}^{n} m_j(f) \Delta x_j$$ where $$m_j(f) := \inf f([x_{j-1}, x_j]) := \inf_{t \in [x_{j-1}, x_j]} f(t) $$

Note that since \(f\) is bounded then by Completeness, \(M_j(f)\) and \(M_j(f)\) exist and are finite. \(M_j(f)\) is the tallest height \(f\) can reach in this interval though it might not be attained since \(f\) is only bounded. For example, take

$$ \begin{align} f(x) = \begin{cases} x, & \text{if } x < 1, \\ 0, & \text{if } x = 1 \end{cases} \end{align} $$

Then the supremum of \(f\) in \([0,1]\) is \(1\) and hence \(M_j = 1\) in that interval. However if \(f\) is continuous, then by EVT, the supremum and infimum are attained in the interval so \(M_j\) and \(m_j\) are now the maximum and minimum. The following is an example of what the Reimann sums would look like:

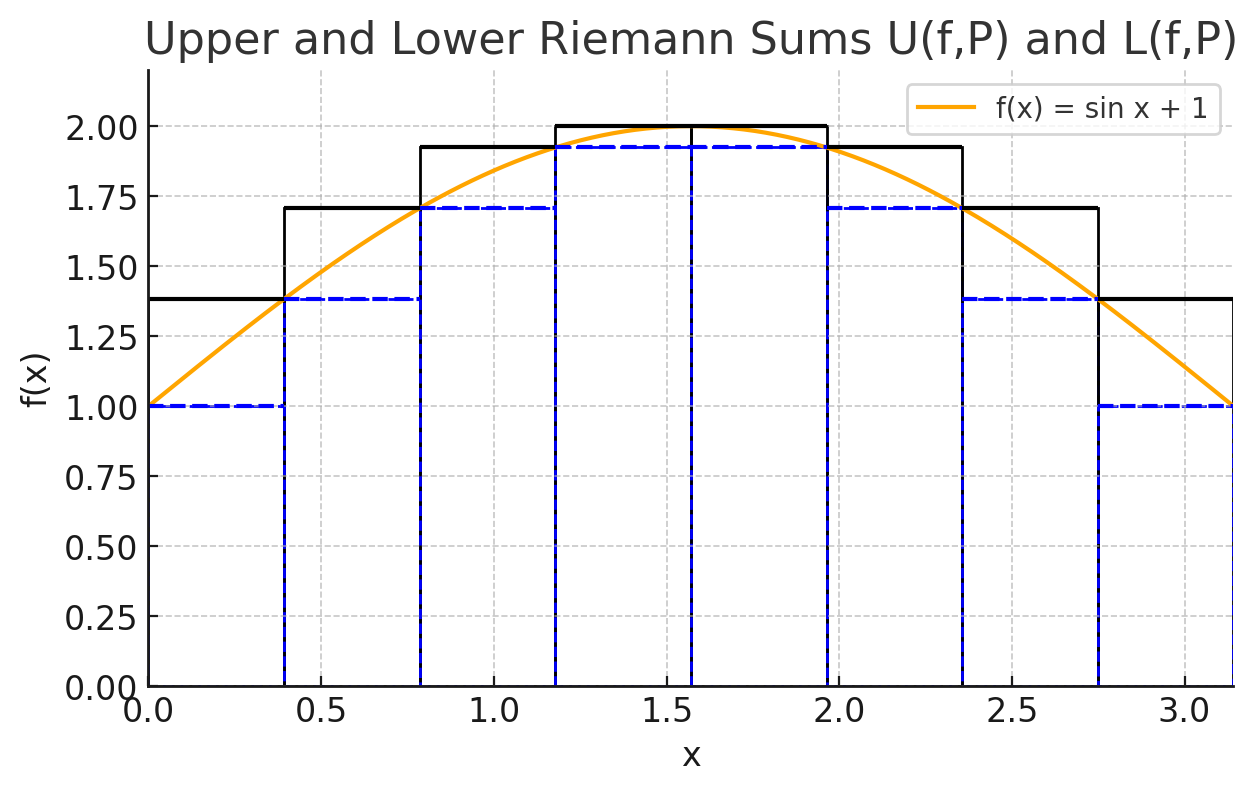
The sum of all the blue rectangles is the lower sum \(L(f,P)\) for the specific partition that we have and the sum of the black rectangles forms the upper Riemann sum for that specific partition.

Definition
We say that \(f\) is Darboux integrable if for all \(\epsilon > 0\), there exists a partition \(P\) such that $$U(f,P) - L(f,P) < \epsilon$$ In particular $$ \begin{align} (U) \int_a^b f(x)dx &= \inf\{U(f,P): P \text{ is any partition of } [a,b]\} \\ (L) \int_a^b f(x)dx &= \sup\{L(f,P): P \text{ is any partition of } [a,b]\} \end{align} $$

So we take all possible Riemann upper sums over all partitions and then take the infimum of that. Then, we do the same for all the possible Reimann lower sums. For example, take

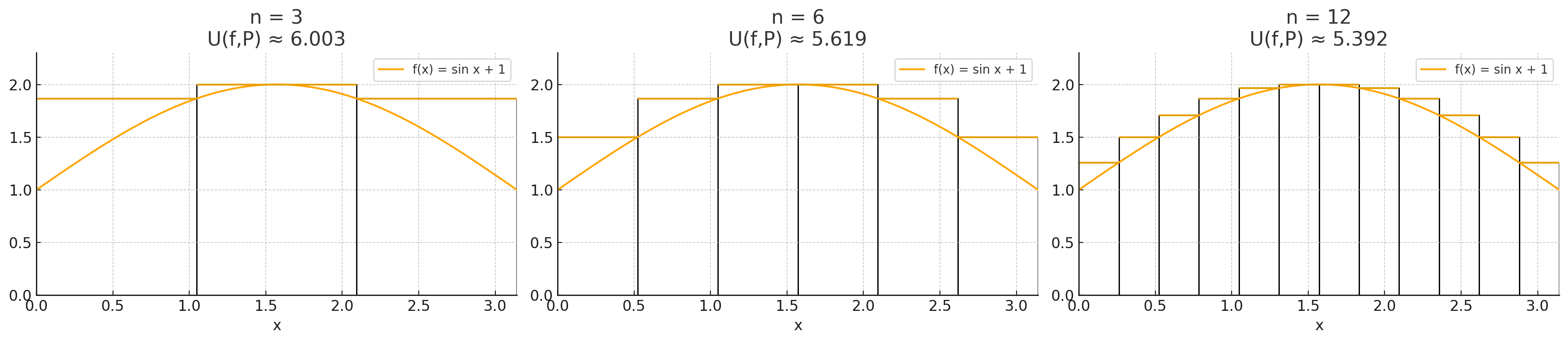
These are three possible partitions and the upper sum for each one. So far the smallest one is the third one. But then we do this for all possible partitions.

References