The Thomae/Popcorn Function
Let $$ \begin{align*} f(x) = \begin{cases} \dfrac{1}{q}, & \text{if } x = \dfrac{p}{q} \in \mathbb{Q} \text{ in lowest terms.} \\[1em] 0, & \text{if } x \in \mathbb{R} \setminus \mathbb{Q}, \end{cases} \end{align*} $$ Then \(f\) is not continuous at any \(x\) such that \(x \in \mathbb{Q}\).

Proof

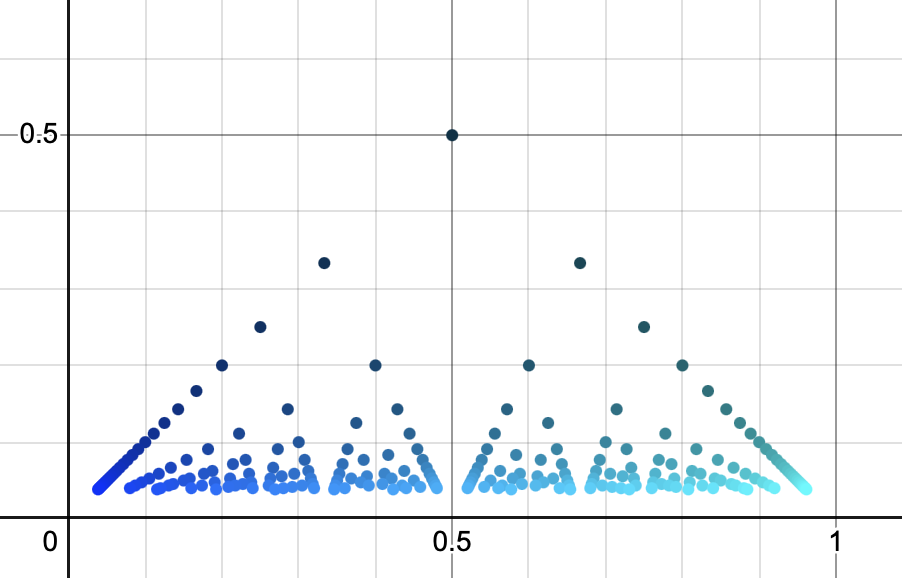
We first claim that \(f\) is not continuous at any rational point. Pick a point \(x_0 = \frac{p}{q} \in \mathbb{Q}\). Since irrationals are dense in \(\mathbb{R}\), then we can find a sequence \(\{x_n\}\) such that

$$ \begin{align*} x_n &\rightarrow x_0 \quad \text{ as } \quad n \to \infty \quad \text{ and } \quad x_n \in \mathbb{R} \setminus \mathbb{Q} \end{align*} $$

We know by definition that \(f(x_n) = 0\). Therefore,

$$ \begin{align*} \lim\limits_{n \to \infty} f(x_n) = 0 \end{align*} $$

Now define the sequence \(\{y_n\}\) by \(y_n = x_0 = \frac{p}{q}\) for all \(n\). Then

$$ \begin{align*} f(y_n) = f\left(\frac{p}{q}\right) = \frac{1}{q} \end{align*} $$

Thus,

$$ \begin{align*} \lim\limits_{n \to \infty} f(y_n) = \frac{1}{q} \end{align*} $$

Since we have two sequences converging to \(x_0\) but \(\lim\limits_{n \to \infty} f(y_n) \neq \lim\limits_{n \to \infty} f(x_n)\). Then \(\lim\limits_{x \to x_0} f(x)\) doesn’t exist. Thus, \(f\) is not continuous at \(x_0\). Since \(x_0\) is chosen arbitrarily, then \(f\) is not continuous at any rational point. \(\ \blacksquare\)

Next, we claim that \(f\) is continuous at any irrational point.

The Thomae/Popcorn Function
Let $$ \begin{align*} f(x) = \begin{cases} \dfrac{1}{q}, & \text{if } x = \dfrac{p}{q} \in \mathbb{Q} \text{ in lowest terms.} \\[1em] 0, & \text{if } x \in \mathbb{R} \setminus \mathbb{Q}, \end{cases} \end{align*} $$ Then \(f\) is continuous at any \(x\) such that \(x \in \mathbb{R} \setminus \mathbb{Q}\).

Strategy

Pick \(x_0 \in \mathbb{R} \setminus \mathbb{Q}\) such that \(x_0 \in [0,1]\) and recall that \(f(x_0) = 0\) by definition. Then
We want to show that for \(\epsilon > 0\), there exists a \(\delta > 0\) such that whenever \(|x - x_0| < \delta\), then

$$ \begin{align*} |f(x) - f(x_0)| &= |f(x) - 0| = |f(x)| < \epsilon \end{align*} $$

The idea of the proof is control what rationals are in the neighborhood of \(|x-\delta|\). It relies on constructing this set

$$ \begin{align*} Q_{q_0} = \left\{ \frac{p}{q} \mid q \leq q_0\right\} \end{align*} $$

For example, \(Q_8 = \{\frac{1}{2}, \frac{1}{3}, \frac{2}{3}, \frac{1}{4},\ldots, \frac{7}{8}\}\) so all the fractions with denominator less that \(q_0 = 8\). This way, if we pick any fraction in \(Q_{q_0}\), then we know that

$$ \begin{align*} f(x) = f\left(\frac{p}{q}\right) = \frac{1}{q} \geq \frac{1}{q_0} \end{align*} $$

On the other hand, if \(x\) is not in the set then

$$ \begin{align*} f(x) = f\left(\frac{p}{q}\right) = \frac{1}{q} < \frac{1}{q_0} \end{align*} $$

Hence, by choosing \(q_0\) to be large enough such that \(\frac{1}{q_0} < \epsilon\), all the rationals with denominator \(q > q_0\) will satisfy \(\frac{1}{q} < \frac{1}{q_0} < \epsilon\).

Proof

Let \(\epsilon > 0\) be given. Pick \(q_0 \in \mathbb{N}\) such that

$$ \begin{align*} \frac{1}{q_0} < \epsilon \end{align*} $$

Consider the set

$$ \begin{align*} Q_{q_0} = \left\{ \frac{p}{q} \in [0,1] \mid q \leq q_0\right\} \end{align*} $$

Then we know that \(|Q_{q_0}| < \infty\) is finite. Since it’s finite, then we can find a \(\delta > 0\) small enough such that

$$ \begin{align*} (x_0 - \delta, x_0 + \delta) \cap Q_{q_0} = \emptyset \quad \quad \quad (1) \end{align*} $$

Then, for all \(x\) such that \(|x - x_0| < \delta\) we have two cases:
Case 1: If \(x \in \mathbb{R} \setminus \mathbb{Q}\), then we know that \(f(x) = 0\). Therefore, \(|f(x) - 0| < \epsilon\).
Case 2: If \(x \in \mathbb{Q}\), then by (1) \(x \in (x_0 - \delta, x_0 + \delta)\). This means that \(x = \frac{p}{q}\) where \(q > q_0\). Thus

$$ \begin{align*} f(x) = f\left(\frac{p}{q}\right) = \frac{1}{q} \leq \frac{1}{q_0} < \epsilon \end{align*} $$

From case 1 and 2, we see that \(f(x) < \epsilon\). Therefore, \(f\) is continuous at \(x_0\). \(\ \blacksquare\)

References