Intermediate Value Theorem
Suppose \(a < b\) and that \(f: [a,b] \to \mathbb{R}\) is continuous. If \(y_0\) lies between \(f(a)\) and \(f(b)\), then there is an \(x_0 \in (a,b)\) such that \(f(x_0) = y_0\).

Notes

One consequence of continuity on a closed and bounded interval, is that any value between \(f(a)\) and \(f(b)\) will get hit, meaning that we can draw the function between \(a\) and \(b\) in one single stroke without lifting the pencil. How do we show this? Suppose we have the following function

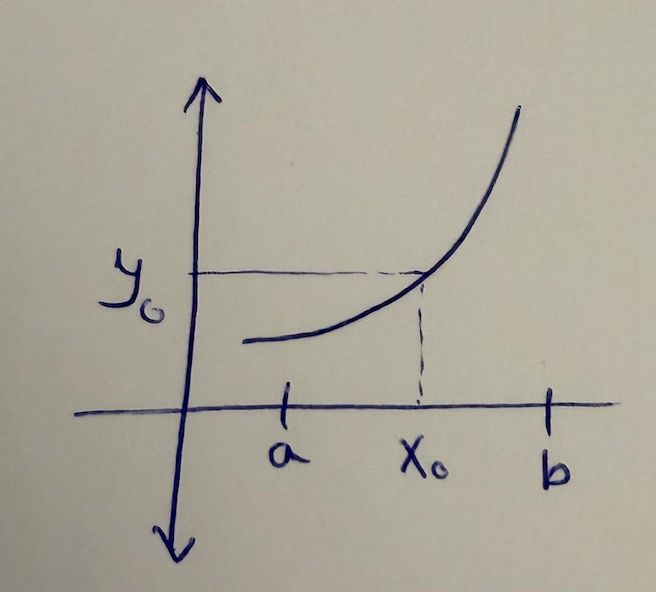
We want to show for any given \(y_0\) between \(f(a)\) and \(f(b)\), we can always find an \(x_0\) such that \(f(x_0) = f(y)\). The idea of the proof is to first translate the function such that \(y_0 = 0\) so \(F(x) = y_0 - f(x)\) as follows:

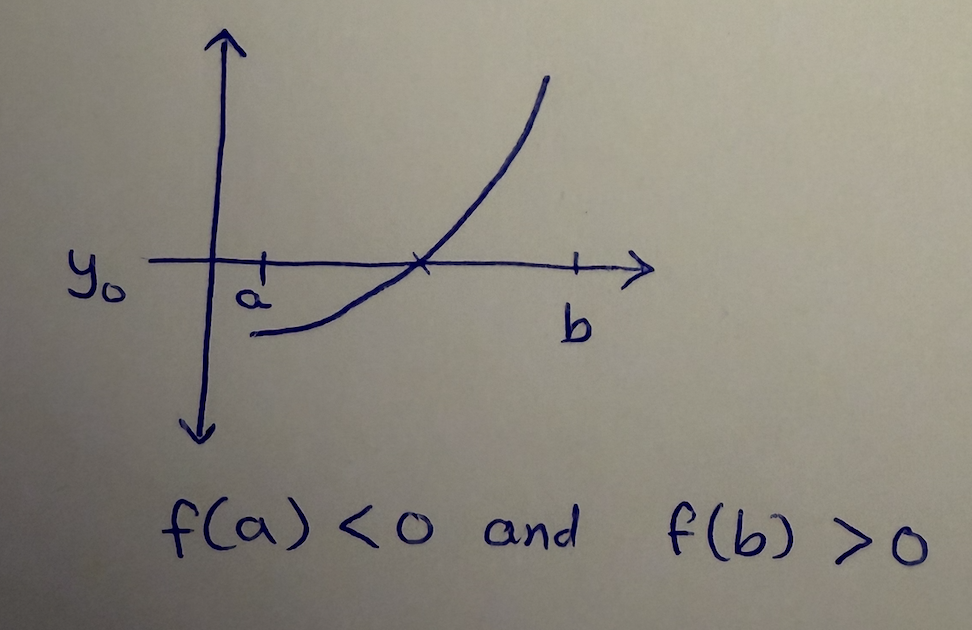
Once we translate the function, notice now that \(f(a) < 0\) and \(f(b) > 0\). Of course if it’s the other way around, we can always mirror the function and consider \(-(y_0-f(x))\). Next is the same idea of the proof of Bolzano-Weirestrass. Take this interval \([a,b]\). Divide it into two halfs. At the mid point, if it’s zero, then we’re done. If not, we want to choose the interval such that the two ends have opposite signs. If we do this over and over again, notice that we will have two sequences. \(\{a_k\}\) and \(\{b_k\}\). But for all \(a_k\), we know that \(F(a_k) < 0\) and for all \(b_k\), we know that \(F(b_k) > 0\). First, by the nested interval property, we know the intersection is a single point \(x\). We also know both sequences must converge to the same intersection point.

Proof

Suppose without the loss of generality that \(f(a) < y < f(b)\). Consider \(F(x) = y - f(x)\). Then

$$ \begin{align*} F(a) &= y - f(a) > 0 \\ F(b) &= y - f(b) < 0 \\ \end{align*} $$

We know \(F\) is continuous on \([a,b]\). Let \(I_1 = [a,b]\) and let \(x_1 = \frac{a+b}{2}\). If \(F(x_1) = 0\), then we’re done. Otherwise, set \(I_2\) as follows

$$ \begin{align*} F(x_1) > 0 \quad \longrightarrow \quad I_2 &= [x_1, b] \\ F(x_1) < 0 \quad \longrightarrow \quad I_2 &= [a, x_1] \end{align*} $$

Suppose now that \(I_k = [a_k, b_k]\) has been constructed for some \(k > 1\) such that \(F(a_k) > 0\) and \(F(b_k) < 0\). Let \(x_{k} = \frac{a_k+b_k}{2}\). If \(F(x_{k}) = 0\), then we’re done. Otherwise, set \(I_{k+1}\) as follows

$$ \begin{align*} F(x_k) > 0 \quad \longrightarrow \quad I_{k+1} &= [x_k, b_k] := [a_{k+1}, b_{k+1}] \\ F(x_k) < 0 \quad \longrightarrow \quad I_{k+1} &= [a_k, b_k] := [a_{k+1}, b_{k+1}] \end{align*} $$

We know that \(F(a_k) > 0\) and \(F(b_k) < 0\) so by construction we know that \(F(a_{k+1}) > 0\) and that \(F(b_{k+1}) < 0\). Observe now that

$$ \begin{align*} I_k \subset \ldots \subset I_3 \subset I_2 \subset I_1 \end{align*} $$

We also know that

$$ \begin{align*} |I_{k+1}| = \frac{|I_{k}|}{2} = \frac{b - a}{2^{k-1}} \end{align*} $$

which implies that

$$ \begin{align*} \frac{b - a}{2^{k-1}} = 0 \quad \text{ as } \quad k \to \infty \end{align*} $$

Thus by the Nested Interval Property, the intersection of all the closed intervals \(I_k\) is non-empty. Furthermore, the intersection contains one point so

$$ \begin{align*} \bigcap_{k = 1}^{\infty} I_k = \{x_0\} \end{align*} $$

Moreover, \(a_k \leq x_0 \leq b_k\) for all \(k\). Hence, \(a_k\) and \(b_k\) converge to \(x_0\). But recall that \(F\) is continuous. Therefore, by the Sequential Characterization of Continuity Theorem,

$$ \begin{align*} F(a_k) \rightarrow F(x_0) \quad \text{ and } \quad F(b_k) \rightarrow F(x_0) \end{align*} $$

But \(F(a_k) > 0\) for all \(k\) so \(F(x_0) \geq 0\) and \(F(b_k) < 0\) for all \(k\) so \(F(x_0) \leq 0\). Hence, \(F(x_0) = 0 = y - f(x_0)\) and \(f(x_0) = y\) as desired. \(\ \blacksquare\)

References

  • Lecture Notes by Professor Chun Kit Lai