Binomial Coefficients Module Prime

First we’re going to look at the binomial coefficients modulo 2. When we build Pascal’s triangle modulo 2, we will get the following diagram.

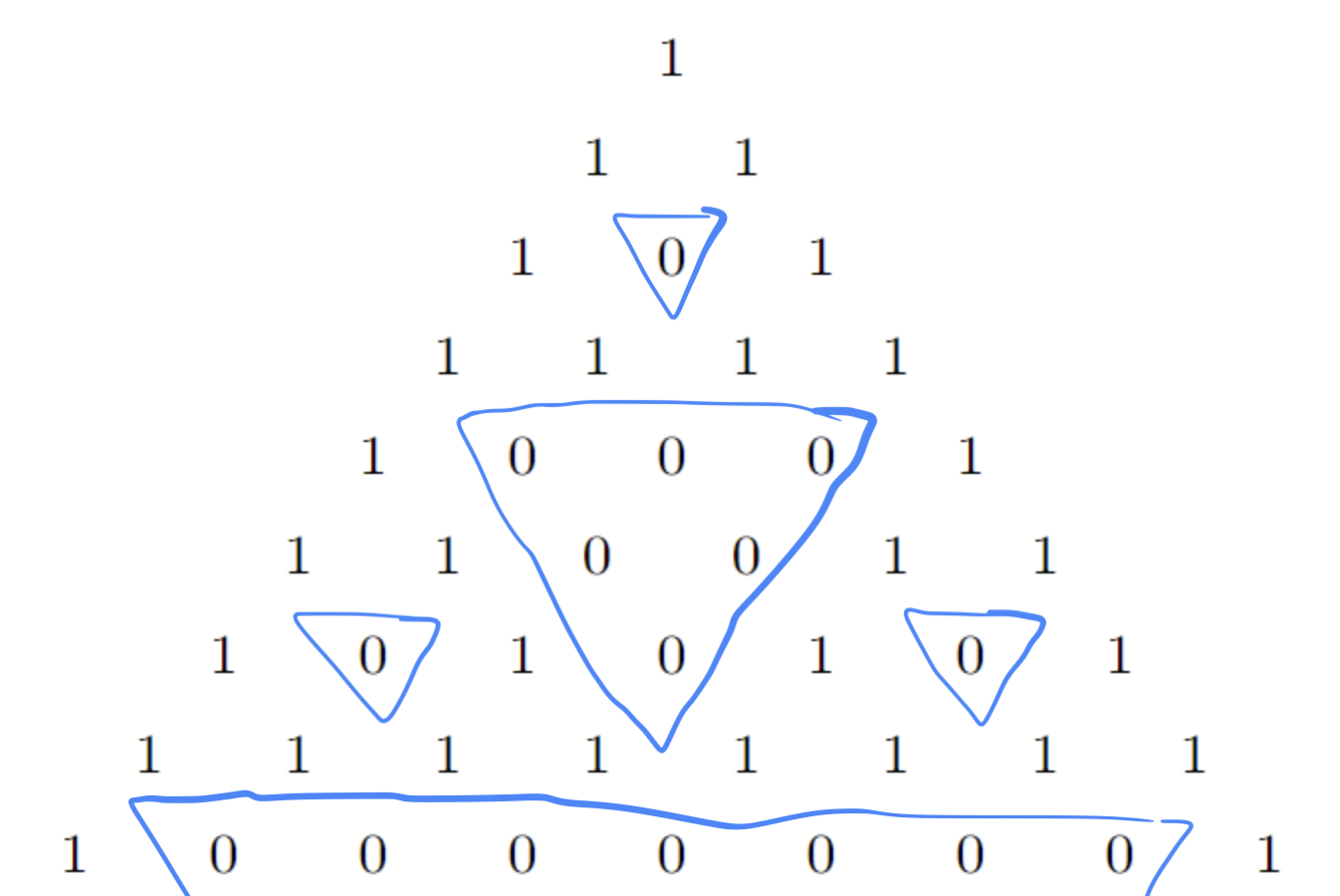
Now, observe the patterns that the zeros are making. One obvious thing to notice is that when the row is a power of 2, almost all coefficients become 0. So now the question is, does this happen for other primes? do rows vanish when they’re divisible by this prime? For example, if we do this for 3. Then we get the following

Note here that the dark square is 2, the light square 1 and the empty squares represent 0. So we do get the same pattern. All the rows divisible by 3 mostly vanish. It turns out, this happens for any prime \(p\). In general

$$ \begin{align*} \binom{p}{k} \bmod p = 0 \quad \text{ if } 0 < k < p. \end{align*} $$

One way to show this is by using the explicit definition

$$ \begin{align*} \frac{p!}{k!}{(p-k)!} \bmod p \end{align*} $$

Observe here that \(p!\) is divisible by \(p\). \(k!\) and \((p-k)!\) are only divisible by \(p\) if \(k = 0\) or \(k = p\). So as long as \(0 < k < p\), we know that \(\binom{p}{k} \bmod p = 0\). This property about primes and binomial coefficients gives us the following application. Consider expanding \((x+y)^p\). Then we would get something like \((x+y)^p = x^p + y^p + p(\)some other term\()\). For example

$$ \begin{align*} (x+y)^5 = x^5 + y^5 + 5(x^4y + 2x^3y^2 + 2x^2y^3 + xy^4) \end{align*} $$

So all the other terms are multiples of 5. So when we take this module 5, you will see that

$$ \begin{align*} (x+y)^5 \bmod 5 = x^5 + y^5 \end{align*} $$

In general,

$$ \begin{align*} (x+y)^p \bmod p = x^p + y^p \end{align*} $$

What about \(p^2\)? observe that

$$ \begin{align*} (x+y)^{p^2} &= [x^p + y^p + p(\cdots)]^p \\ &= x^{p^2} + y^{p^2} + p(\cdots)^p \end{align*} $$

Thus

$$ \begin{align*} \binom{p^2}{k} \bmod p = 0 \quad \text{ if } 0 < k < p. \end{align*} $$

# of Times a Prime Divides a Binomial Coefficient

Sometimes it is useful to know how many times does a prime divides a binomial coefficient. Recall that the explicit definition is \(\binom{n}{k} = \frac{n!}{(n-k)!}\). First, take the numerator. How many times does \(p\) divide \(n!\)? For example, how many times does 2 divide \(8!\)? Write the expansion of \(8!\) as follows

$$ \begin{align*} 8! = 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \end{align*} $$

We have 4 even numbers. Each one of them divides 2. So we have \(2^4\) as a factor. We can add an extra factor of 2 for \(4\) and \(8\). Finally, we still need to a final factor of 2 for 8. So we have \(2^7\). In general, if we want to know how many times does \(p\) divide \(n!\), then we list the numbers from \(1\) all the way to \(n\) which will include numbers divisible by \(p\) like \(p\) itself, \(2p\) and other multiples of \(p\). So

$$ \begin{align*} 1, 2, 3, \cdots, p, \cdots ,2p, \cdots ,(n-1), n \end{align*} $$

Intuitively, it is easy to see that we just need to know how many copies of \(p\) are \(n\). In fact, there are \([\frac{n}{p}]\) copies where \([]\) means the integer part of the number. That’s not everything though since \(p^2\) is also divisible by \(p\) so we want to count all the copies of \(p^2\) as well and that’s \([\frac{n}{p^2}]\). Similarly, we need to count the number of copies of \(p^3\), \(p^4\) and so. Thus, the total number of times \(p\) divides \(n!\) is

$$ \begin{align*} \left[\frac{n}{p}\right] + \left[\frac{n}{p^2}\right] + \left[\frac{n}{p^3}\right] + \cdots \end{align*} $$

Observe now that this sum is slightly less than the geometric series

$$ \begin{align*} \left[\frac{n}{p}\right] + \left[\frac{n}{p^2}\right] + \left[\frac{n}{p^3}\right] + \cdots < \frac{n}{p} + \frac{n}{p^2} + \frac{n}{p^3} \cdots = \frac{n}{p-1}. \end{align*} $$

Example 1

Take 1000! how many zeros does it have? so we want to count how many times does 2 divide 1000! and also how many times does 5 divide this number. The number of times 5 divides 1000! is

$$ \begin{align*} \left[\frac{1000}{5}\right] + \left[\frac{1000}{5^2}\right] + \left[\frac{1000}{5^3}\right] + \left[\frac{1000}{5^4}\right] \end{align*} $$

But note here that once we compute \(\left[\frac{1000}{5}\right] = 200\), then for the next computation, we just divide this number by 5 again.

$$ \begin{align*} 200 + \left(\left[\frac{200}{5}\right]=40\right) + \left(\left[\frac{40}{5}\right]=8\right) + \left(\left[\frac{8}{5}\right]=1\right) = 249 \end{align*} $$

Similarly for 2,

$$ \begin{align*} \left[\frac{1000}{2}\right]&=500 \\ \left[\frac{500}{2}\right]&=250 \\ \left[\frac{250}{2}\right]&=125 \end{align*} $$

But we don’t need to continue dividing as we have already passed the count of 249 in step 1. We stop since now we have exactly 249 zeros.

Example 2

Suppose we want to find the number of times 7 divides \(\binom{100}{40}\). The number of times 7 divides 100 is

$$ \begin{align*} \left[\frac{100}{7}\right]&=14 \\ \left[\frac{14}{7}\right]&=2 \end{align*} $$

So we have 7 dividing 100 16 times. While the number of times 7 divides 40 is

$$ \begin{align*} \left[\frac{40}{7}\right]&=5 \end{align*} $$

is just 5 times. Finally, the number of times 7 divides 7 is

$$ \begin{align*} \left[\frac{60}{7}\right]&=8 \\ \left[\frac{8}{7}\right]&=1 \end{align*} $$

So it’s 9 times. Thus, the number of times 7 divides \(\binom{100}{40}\) is \(16 - 5 - 9 = 2\).

How Big are Binomial Coefficients?

A crude estimate would be to look at the sum of the \(n\)th row in Pascal’s triangle which we found in the last lecture to be \(2^n\). Thus

$$ \begin{align*} \binom{n}{k} \leq 2^n \end{align*} $$

We can also give a lower bound by observing that

$$ \begin{align*} 2^{2n} = \binom{2n}{0} + \binom{2n}{1} + \cdots + \binom{2n}{n} + \cdots + \binom{2n}{2n} \end{align*} $$

and noticing here that we have exactly \(2n+1\) terms and that \(\binom{2n}{k}\) is the largest coefficient among these \(2n+1\) coefficients. If we assume that every single coefficient is as large as the largest one, then

$$ \begin{align*} 2^{2n} &\leq (2n+1) \binom{2n}{n} \end{align*} $$

which then gives us the bound

$$ \begin{align*} 2^{2n} \geq \binom{2n}{n} \geq \frac{2^{2n}}{(2n+1)} \end{align*} $$

We can also use Stirling’s Formula to precisely compute the binomial coefficients using

$$ \begin{align*} n! \approx n^{n+\frac{1}{2}}e^{-n}\sqrt{2\pi} \end{align*} $$

An Upper Bound on the Number of Primes \(\leq n\)?

As an application, we can try to estimate how many primes are there that are less than or equal to \(n\). Let the number of primes \(\leq n\) be \(\pi(n)\). The prime number theorem gives us the estimate of \(\pi(n) \approx \frac{n}{\log n}\). However, the prime number theorem is difficult to prove. So we will instead use the binomial coefficients to prove a slightly weaker version of it as follows

$$ \begin{align*} \frac{1}{2} \frac{n}{\log n} \leq \pi(n) \leq 2\frac{n}{\log n} \end{align*} $$

The key idea is to look at the binomial coefficient of \(\binom{2n}{n}\) and the number of primes diving it. So suppose that \(2 < p < 2n\). Then \(p\) divides \(\binom{2n}{n}\) exactly once. why?

$$ \begin{align*} \binom{2n}{n} = \frac{2n!}{(2n-n)!n!} = \frac{2n!}{n!n!} \end{align*} $$

\(p\) divides \(2n!\) but it doesn’t divide \(n!\). So \(p\) divides \(\binom{2n}{n}\) once. Now, take the product of all primes \(p\) between \(2\) and \(2n\). Each one of these primes divides \(\binom{2n}{n}\) once. so their product must divide \(\binom{2n}{n}\) as well

$$ \begin{align*} \prod_{2 < p < 2n} p \mid \binom{2n}{n} \end{align*} $$

And this gives the lower bound below

$$ \begin{align*} \prod_{2 < p < 2n} p \leq \binom{2n}{n} \end{align*} $$

But we already saw earlier that we can also bound \(\binom{2n}{n}\) as follows

$$ \begin{align*} \prod_{2 < p < 2n} p \leq \binom{2n}{n} \leq 2^{2n} \end{align*} $$

So now let’s take the log of each side

$$ \begin{align*} \sum_{2 < p < 2n} \log p \leq 2n \log 2 \end{align*} $$

Now, for any prime \(p\) in the interval \([n,2n]\), we know that \(p \geq n\). Thus, \(\log p \geq \log n\). Let \(\pi(n,2n)\) be the number of primes in the interval \([n,2n]\). Then, the sum of logarithms of primes in the interval \([2,2n]\) is at least:

$$ \begin{align*} \sum_{2 < p < 2n} \log p \geq \pi(n,2n) \cdot \log n \end{align*} $$

This gives us the inequality

$$ \begin{align*} \pi(n,2n) \cdot \log n &\leq 2n \log 2 \end{align*} $$

We can now solve for the number of primes to see that

$$ \begin{align*} \pi(n,2n) &\leq \log 2 \cdot \frac{2n}{\log n} \end{align*} $$

But then with some additional work (TODO?), we can get to

$$ \begin{align*} \pi(n) &\leq \frac{2n}{\log n} \end{align*} $$

A Lower Bound on the Number of Primes \(\leq n\)?

What about a lower bound on the number of primes? We will again look at the binomial coefficient \(\binom{2n}{n}\). If we take the product of all prime powers less than \(2^n\), then we will get the following bound (WHY?)

$$ \begin{align*} \prod_{p^k \leq 2n} p \geq \binom{2n}{n} \end{align*} $$

[The left hand side is the product of \(k\) copies of \(p\) where \(p^k \leq 2n\).] The number of times \(p\) divides \(\binom{2n}{n}\), can be done similar to example 2. Since \(\binom{2n}{n} = \frac{(2n)!}{n!n!}\), then

$$ \begin{align*} &=\left[\frac{2n}{p}\right] - \left[\frac{n}{p}\right] - \left[\frac{n}{p}\right] \\ &+ \left[\frac{2n}{p^2}\right] - \left[\frac{n}{p^2}\right] - \left[\frac{n}{p^2}\right] \\ &+ \cdots \end{align*} $$

However, observe here that the expression \(\left[\frac{2n}{p}\right] - \left[\frac{n}{p}\right] - \left[\frac{n}{p}\right]\) is either 0 or 1 since it is equal to \([2n] - [n] - [n]\) and this is always 1 or 0 depending on the fractional part of \(n\). This means that in the inequality above, for each power of \(p\), we’re going to see that we will get at most 1 copy of \(p\) dividing \(\binom{2n}{n}\). Therefore, the product \(\prod_{p^k \leq 2n} p\) is at least bigger than \(\binom{2n}{n}\).

Furthermore, we saw earlier that that

$$ \begin{align*} \binom{2n}{n} \geq \frac{2^{2n}}{2n+1} \end{align*} $$

Combining both inequalities and then taking the logarithms of both sides

$$ \begin{align*} \prod_{p^k \leq 2n} p &\geq \frac{2^{2n}}{2n+1} \\ \log \prod_{p^k \leq 2n} p &\geq \frac{2^{2n}}{2n+1} \\ \sum_{p^k \leq 2n} \log p &\geq 2n\log 2 - \log(2n+1) \end{align*} $$

So now how do we turn \(\sum_{p^k \leq 2n} \log p\) to counting primes? We need to simplify things further. First, the terms \(p^2\), \(p^3\), and so on are small. Second, \(\log(x)\) is almost constant as \(n\) gets really big. Therefore, \(\log p \approx \log 2n\) for most primes. Thus

$$ \begin{align*} \sum_{p \leq 2n} 2n &\geq 2n\log 2 - \log(2n + 1) \end{align*} $$

In other words,

$$ \begin{align*} \pi(2n) &\geq \frac{2n\log 2}{\log 2n} - \text{small factors} \end{align*} $$

Catalan Numbers

Take a look at the binomial coefficient \(\binom{2n}{n}\) again. If we write them down, we will get

$$ \begin{align*} 1 \ \ 2 \ \ 6 \ \ 20 \ \ 70 \ \ \cdots \end{align*} $$

which we notice that they are divisible by

$$ \begin{align*} 1 \ \ 2 \ \ 3 \ \ 4 \ \ 5 \ \ \cdots \end{align*} $$

so \(\binom{2n}{n}\) is always divisible by \(n+1\). The sequence we get after dividing is

$$ \begin{align*} 1 \ \ 1 \ \ 2 \ \ 5 \ \ 14 \ \ \cdots \end{align*} $$

This sequence is called the Catalan numbers. They are famous because they count many things. For instance, they count the number of ways to bracket products. So to count the ways to multiply \(abcd\), we will see that there are exactly 5 ways.

$$ \begin{align*} (((ab)c)d) \quad a(b(cd)) \quad (ab)(cd) \quad (a(bc))d \quad a((bc)d) \end{align*} $$

Why is this true? Catalan numbers can be described with the following

$$ \begin{align*} C_0 &= 1 \\ C_n &= C_0C_{n-1} + C_1C_{n-2} + C_2C_{n-3} + \cdots + C_{n-1}C_0 \end{align*} $$

So if we’re multiply \(n\) numbers together, we can imagine that \(C_0\) represents \(a\), \(C_1\) represents \(ab\), \(C_2\) represents \(abc\) and we can start pairing them as follows

$$ \begin{align*} (a(...)) \quad (ab)(...) \quad (abc)(...) \quad \cdots \end{align*} $$

How did the recurrence formula for Catalan numbers came to? For this we again use the powerful tool of generating numbers. So if we let

$$ \begin{align*} f(x) = C_0 + C_1x + C_2x^2 + \cdots \end{align*} $$

Then

$$ \begin{align*} f(x)^2 = C_0^2 + (C_1C_0 + C_0C_1)x + (C_0C_2+C_1C_1+C_2C_0)x^2 + \cdots \\ \end{align*} $$

In fact,

$$ \begin{align*} 1 + xf(x)^2 = f(x) \end{align*} $$

This is a quadratic equation where we can use the quadratic formula to solve it and get

$$ \begin{align*} f(x) = \frac{1 \pm \sqrt{1 - 4x}}{2x} \end{align*} $$

But now recall that

$$ \begin{align*} (1 + x)^n = 1 + \binom{n}{1}x + \binom{n}{2}x^2 + \cdots + \binom{n}{n}x^n \end{align*} $$

and this works even if \(n\) is not an integer. So we can use this to expand \(\sqrt{1 - 4x}\) in the quadratic formula above. So

$$ \begin{align*} (1 - 4x)^{1/2} = \sum_{n=0} \binom{1/2}{n} (-4x)^n \end{align*} $$

If we work this out, we will see that this turns out to be

$$ \begin{align*} \frac{1 - (1 - 4x)^{1/2}}{2x} &= \sum_{n} \frac{(2n-2)!}{n!(n-1)!}x^{n-1} \\ &= \sum_{n} x^n \frac{\binom{2n}{n}}{n+1} \\ &= \sum_{n} C_nx^n \end{align*} $$

References