Theorem
Squareroot of \(2\) exists. It is \(s = \sup \{x \in \mathbb{R}^{+} \mid x^2 < 2\}\) where \(s^2 = 2\).

Strategy

Let \(E = \{x \in \mathbb{R}^{+} \mid x^2 < 2\}\) and let \(s = \sup(E)\). We want to show that \(s^2 = 2\). This will mean that that the supremum itself is the “Square root of \(2\)”. We do this by showing that it’s impossible for \(s^2\) be greater than \(2\) or less than \(2\) so it must be \(2\). Then, we have two cases.

Case 1: \(s^2 < 2\): Here, we want to show that it’s impossible to have \(s^2 < 2\). Why? because \(s\) is now going to be too small to be the square root of \(2\) or the supremum. This is because we will be able to find a number slightly larger than \(s\) and have its square be less than \(2\) still which means it’s in the set. This is a contradiction since now \(s\) is no longer the supremum.

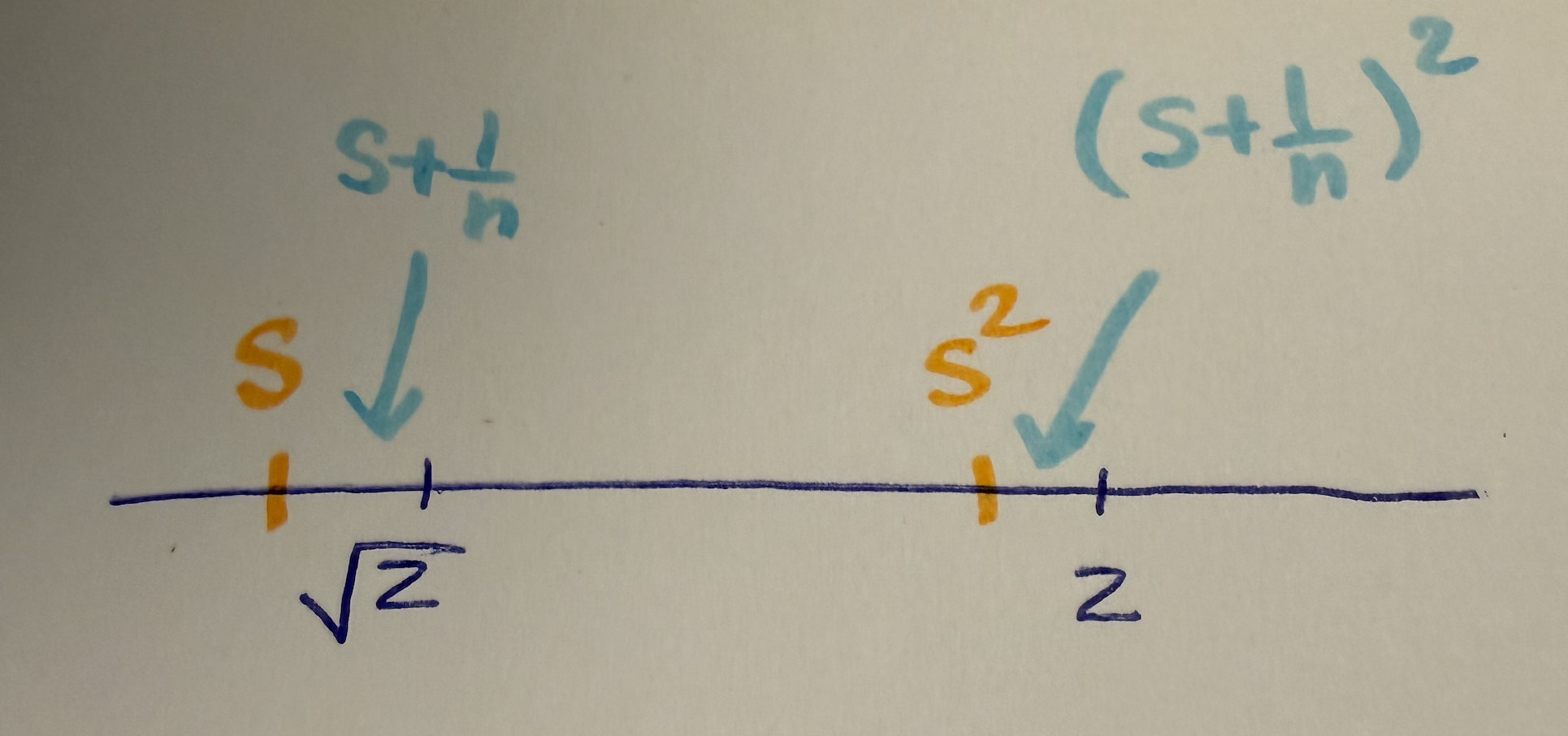
To show this:

  1. We can pick a number that is slightly bigger than \(s\). Let this number be \(s + \frac{1}{n}\).
  2. When we square this number, then \((s+\frac{1}{n})^2\) is still going to be under \(2\).
  3. This means that \(s+\frac{1}{n}\) belongs in the set \(E\). This is a contradiction since we said that \(s\) is the supremum.

So we can go back to point \(2\) and derive what \(n\) should be

$$ \begin{align*} 2 &> \left(s+\frac{1}{n}\right)^2 \\ 2 &> s^2 + \frac{2s}{n} + \frac{1}{n^2} \\ 2 &> s^2 + \frac{2s}{n} + \frac{1}{n^2}. \end{align*} $$

What do we do with \(\frac{1}{n^2}\)? The goal is to show that \(\left(s+\frac{1}{n}\right)^2\) is less than \(2\). So if we show that a bigger fraction is less than \(2\), then automatically, \(\left(s+\frac{1}{n}\right)^2\) is less than \(2\). So the idea here is to replace \(\frac{1}{n^2}\) with a bigger number to make it simpler. So let’s replace it with \(\frac{1}{n}\). Notice how \(\frac{1}{n} > \frac{1}{n^2}\). So this makes the new fraction bigger.

$$ \begin{align*} 2 &> s^2 + \frac{2s}{n} + \frac{1}{n} \\ 2 - s^2 &> \frac{2s}{n} + \frac{1}{n} \\ 2 - s^2 &> \frac{2s + 1}{n} \\ n &> \frac{2s + 1}{2 - s^2} \\ \end{align*} $$

So now if we choose this \(n\) (using the Archimedean principle), then we will guarantee this fraction to be less than \(2\) which is what we want.

Case 2: For case 2, we have \(s^2 > 2\) and this picture

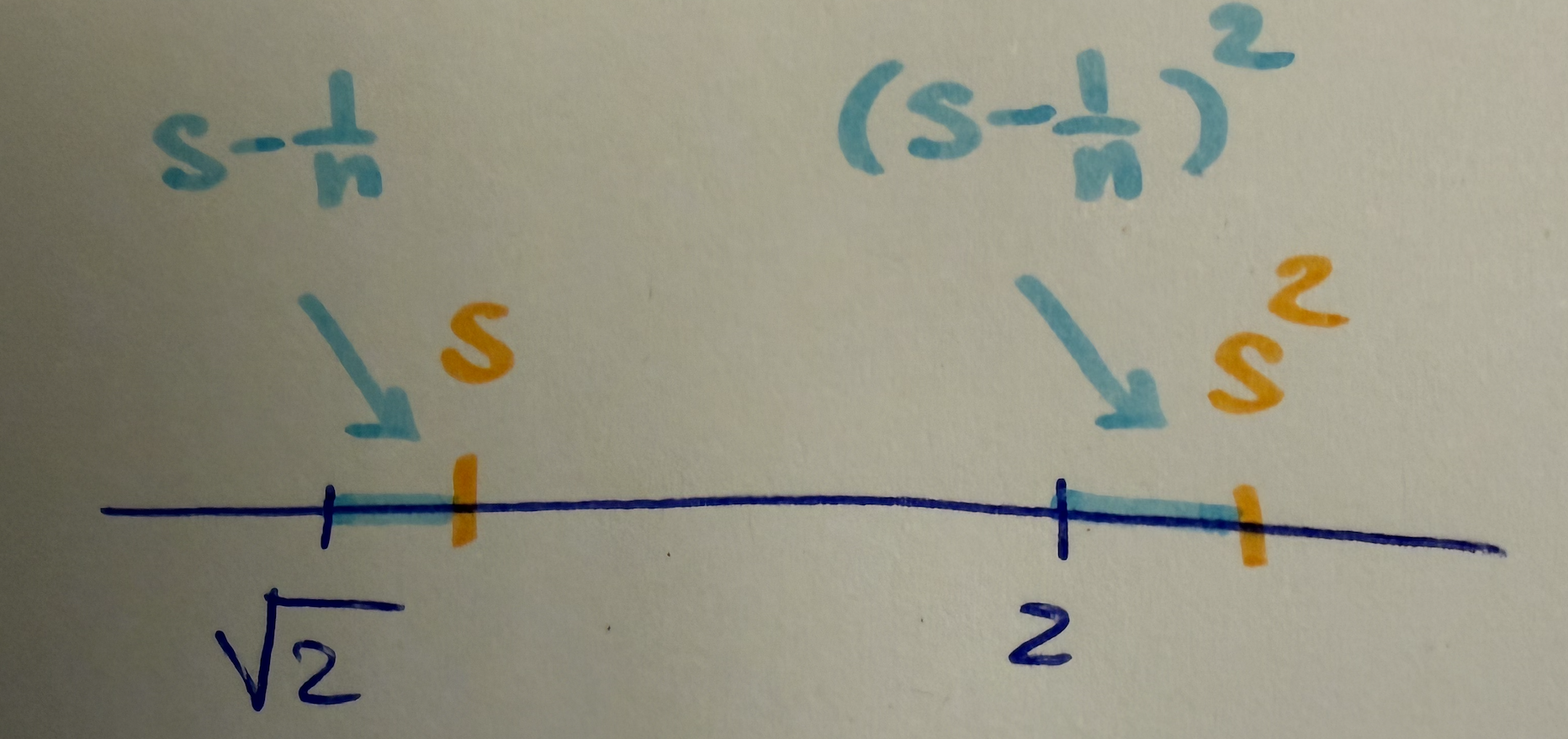
We want to show that if \(s^2 > 2\), then we will be able to pick a slightly smaller \(s\) and we will show that this smaller \(s\) is actually an upper bound on \(E\). But it’s smaller and it’s an upper bound, then \(s\) is not a supremum so that’s a contradiction and \(s^2 \not> 2\). To derive this \(n\), then

$$ \begin{align*} \left(s-\frac{1}{n}\right)^2 &= s^2 - \frac{2s}{n} + \frac{1}{n^2} > 2 \end{align*} $$

We want to show that this quantity is greater than \(2\). So here it’s the opposite. To ensure it’s greater than \(2\), we want a weaker simpler quantity (not a bigger one). So notice now that if we remove \(\frac{1}{n^2}\), then this quantity will be smaller.

$$ \begin{align*} s^2 - \frac{2s}{n} + \frac{1}{n^2} &> s^2 - \frac{2s}{n}. \end{align*} $$

and what we want is this to have this smaller quantity to be larger than \(2\). In particular we want

$$ \begin{align*} s^2 - \frac{2s}{n} &> 2 \\ s^2 - 2 &> \frac{2s}{n} \\ \frac{1}{s^2 - 2} &< \frac{n}{2s} \\ \frac{2s}{s^2 - 2} &< n \end{align*} $$

We can now again use the Archimedean property to get that \(n\).

To recap, in case \(1\) where \(s^2 < 2\). Here, we will find an element in the set that’s greater than \(s\) which is a contradiction. In case \(2\), \(s^2 > 2\), we will be able to find a better bound than \(s\) itself so \(s\) can no longer be a supremum.

Proof

Let \(E = \{x \in \mathbb{R}^{+} \mid x^2 < 2\}\) and let \(s = \sup(E)\). We want to show that \(s^2 = 2\). Suppose for the sake of contradiction that \(s^2 \neq 2\). We have two cases.
Case 1: \(s^2 < 2\). Then we know that \(2 - s^2 > 0\). Therefore \(\frac{2s + 1}{2 - s^2} > 0\). Thus, by the Archimedean principle, we can pick \(n\) such that

$$ \begin{align*} n &> \frac{2s + 1}{2 - s^2} \end{align*} $$

This implies that

$$ \begin{align} 2 - s^2 &> \frac{2s + 1}{n} \\ 2 &> s^2 + \frac{2s + 1}{n} \end{align} $$

Observe now that

$$ \begin{align*} \left(s+\frac{1}{n}\right)^2 &= s^2 + \frac{2s}{n} + \frac{1}{n^2} \\ &< s^2 + \frac{2s}{n} + \frac{1}{n} \\ &= s^2 + \frac{2s + 1}{n} \\ &< 2. \quad \text{(By the previous inequality)} \end{align*} $$

This shows that \(\left(s+\frac{1}{2}\right)^2 < 2\). So \(s+\frac{1}{n} \in E\). This is a contradiction since \(s\) is the supremum of the set by assumption. Therefore, \(s^2 \not< 2\).

Case 2: \(s^2 > 2\). Then we know that \(s^2 - 2 > 0\) and so \(\frac{2s}{s^2 - 2} > 0\). By the Archimedean principle, choose \(n\) such that

$$ \begin{align*} n > \frac{2s}{s^2 - 2} \end{align*} $$

This implies that

$$ \begin{align*} s^2 - 2 > \frac{2s}{n} \\ s^2 - \frac{2s}{n} &> 2 \end{align*} $$

Now, observe that

$$ \begin{align*} (s - \frac{1}{n})^2 &= s^2 - \frac{2s}{n} + \frac{1}{n^2} \\ &> s^2 - \frac{2s}{n} \\ &> 2 \quad \text{(By the previous inequality)} \\ \end{align*} $$

This shows that \(s - \frac{1}{n}\) is an upper bound on \(E\). This is a contradiction since \(s\) is the supremum of \(E\). Therefore, \(s^2 \not<2\). Thus, by case 1 and case 2, we must have \(s^2 = 2\). \(\ \blacksquare\)

References

  • Lecture Notes by Professor Chun Kit Lai