Proof (1, Lecture/Textbook)
Strategy
We want to find a rational number \(\frac{m}{n}\) such that \(a < \frac{m}{n} < b\). Suppose that \(0 < a < b\). Now construct the set
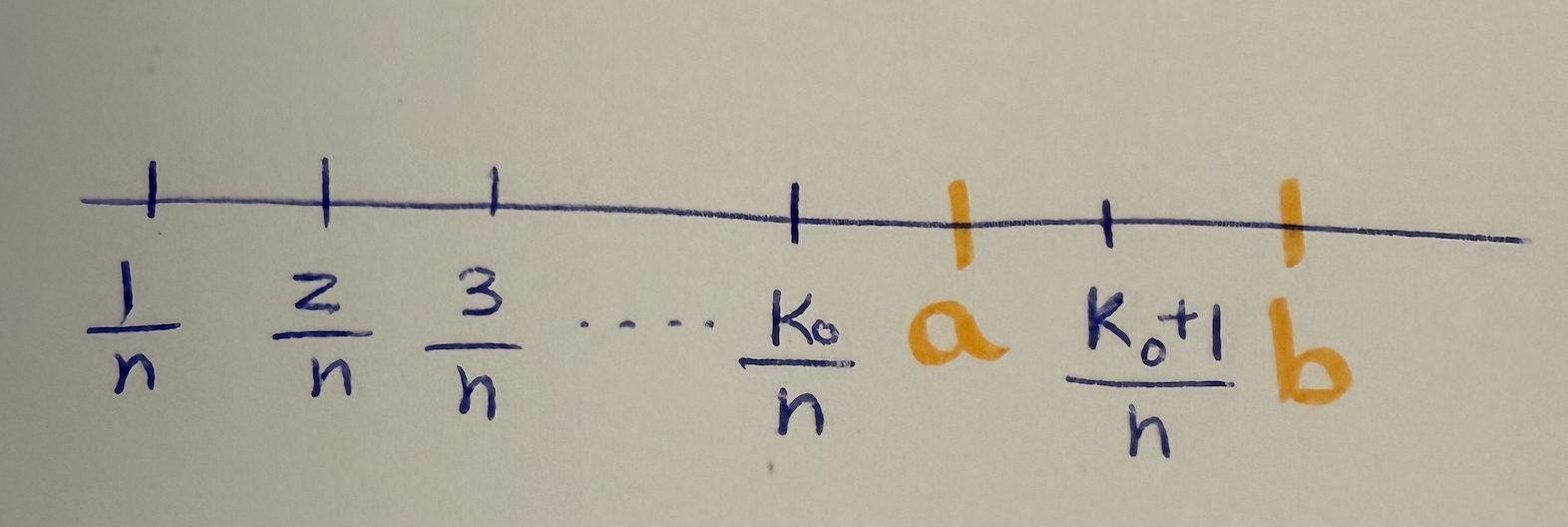
So we’re walking in steps of size \(\frac{1}{n}\). Note that \(S \subset \mathbb{N}\). If we let \(k_0 = \sup(E)\), then we know that \(k_0 \in E\) and \(k_0 + 1\) is not in \(E\). But this implies that \(\frac{k_0+1}{n} > a\). So we have a potential fraction that is strictly greater than \(a\). We still want to make this fraction be strictly less than \(b\) just like the picture above.
How can we do it? We can derive what \(n\) needs to be since \(n\) is fixed. We specifically want that
But this means that we want \(n\) to be
So the construction of the set ensures that the element that comes right after the supremum is greater than \(a\). But this relies on the set not being empty. To ensure this, we also want to make sure that \(n \geq \frac{1}{a}\). The second condition that we just derived ensures that this element is strictly less than \(b\). Hence, we have found a rational number in between \(a\) and \(b\).
Formal Proof
Case 1: \(a < 0 < b\): This is the trivial case since \(0 \in \mathbb{Q}\).
Case 1: \(0 < a < b\): By the Archimedean principle, choose \(n\) such that
From this, we get that
Now, consider the set
Observe that \(1 \in E\). Therefore, \(E\) is non-empty. Moreover, \(E\) is bounded by definition. By the completeness axiom, there exists a supremum of \(E\). Let \(k_0 = \sup(E)\) and so \(k_0+1 \not\in E\). By the definition of \(E\), this implies that
So this establishes that the fraction is strictly greater than \(a\). Next, we want to show that it is less than \(b\). To see this observe that
Case 3: \(a < b < 0\): Multiply the inequality by \(-1\) to see that
Now let \(a' = -a\) and \(b' = -b\) to get
Then, by case 1, we know we can find
So just multiply this by \(-1\) to get
Then, \(-\frac{k_0 + 1}{n} \in \mathbb{Q}\) as required. \(\ \blacksquare\)
Proof (2, Dr. Peyam)
Suppose that \(a < b\) and assume that \(0 < a < b\). Since \(a < b\), then we know that \(b - a > 0\). Since \(b - a\) is a positive number, then by the Archimedean Principle (with \(x = b-a\) and \(y = 1\)), we can always find \(n \in \mathbb{N}\) such that
which implies that
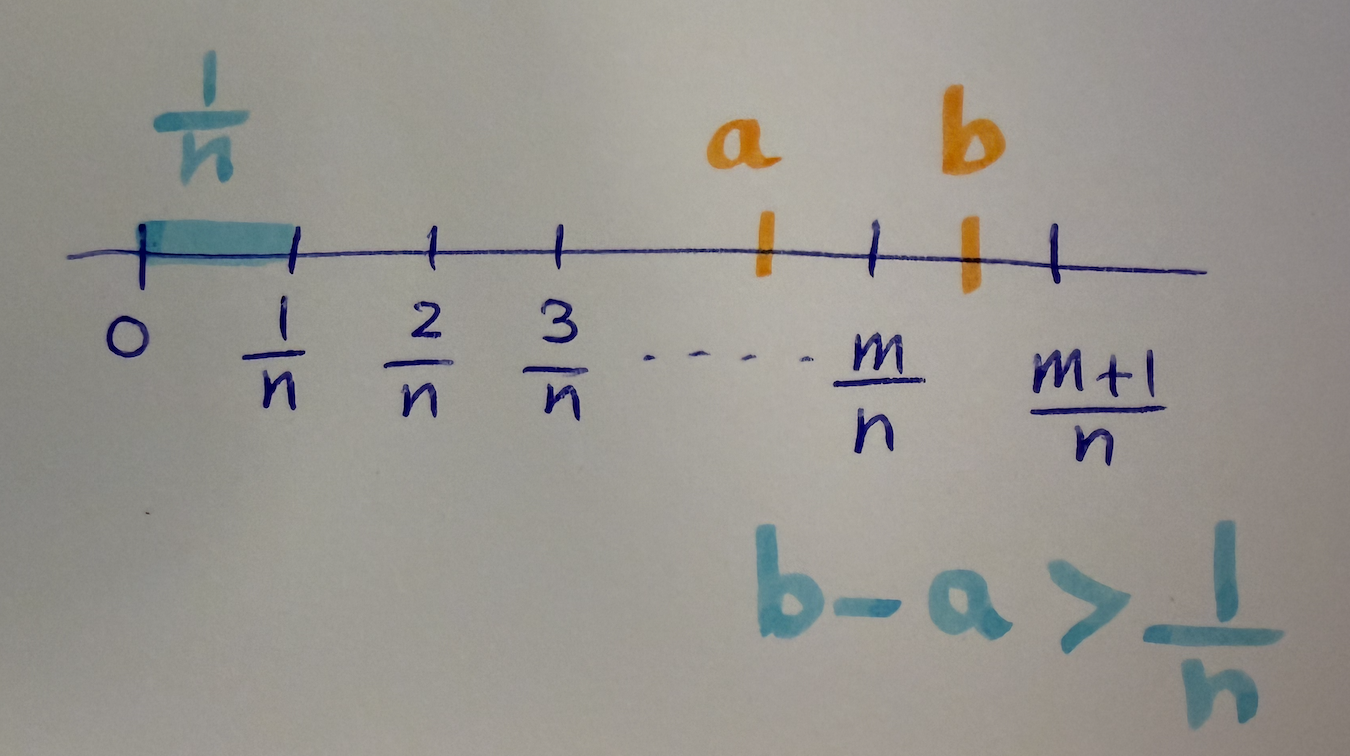
So let
We know that \(S\) is non-empty since \(0 \in S\) because \(b > 0\). Moreover, \(S\) is bounded above by \(b\). Therefore, by the completeness axiom, \(S\) has a least upper bound. So let \(r = \sup(S)\). We claim that \(a < r < b\). Observe that \(S\) is finite. This means that \(r = \sup(S) = \max(S)\). But since it’s the maximum element, then \(r \in S\). So \(r\) is rational. By definition, we know that \(r < b\). So the only thing left to show is that \(r \geq a\).
Suppose for the sake of contradiction that \(r = \frac{m}{n} \leq a\). We know that
Since \(r = \frac{m}{n} \leq a\), then
But this implies that \(\frac{m+1}{n} \in S\). This is a contradiction since \(\sup(S) = \frac{m}{n}\). Then we must have that \(r = \frac{m}{n} < a\). \(\ \blacksquare\)
References