Today we will discuss a formula for counting orbits calling the burnside formula. The book illustrates this with a necklace beads counting example. So how many necklaces are there with two orange, two blue beads? If we count naively, we have 4 slots. The two blue beads will go into two of the slots. So there are \(\binom{4}{2} = 6\) to do this. Then the orange beads will get the remaining two spots. So

$$ \begin{align*} X = \{OOBB, OBOB, OBBO, BOBO, BOOB, BBOO\} \end{align*} $$

But that’s not right. There are only 2 distinct elements. This in fact is the same as counting orbits of a group action. 2 here is the number of orbits of a group action. The group action is

$$ \begin{align*} G = \{ D_4 \}, |G| = 8 \quad \text{acts on } X = \text{ The set of linear arrangements where $|X|=6$} \end{align*} $$

To see this, imagine the beads moving by 90 degrees (which is the rotation \(r\)) to get the next shape in the picture. The symmetries of the beads are the same as the symmetries of the dihedral group. We can also flip the necklace on the \(x\)-axis which is the same as the flip \(j \in D_4\). Now, the orbits of this action are as follows

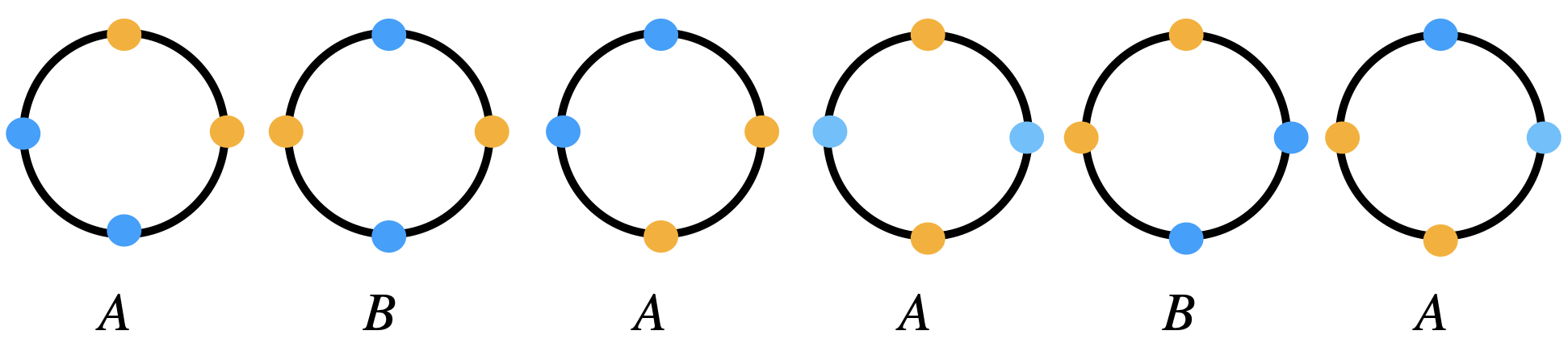
$$ \begin{align*} A &= \{OOBB, OBBO, BOOB, BBOO\} \\ B &= \{OBOB, BOBO\} \end{align*} $$



Example 2

How many necklaces with 9 beads: 4 red, 3 white, 2 yellow? This isn’t an easy question. But there is an easier question which is counting the linear arrangements of the 9 beads with the colors we have. Let \(X\) be the set of linear arrangements of 9 beads with 4 red, 3 while, 2 yellow. If they were all of different colors, then there will be \(9!\) arrangements. But only have 3 colors so some of the beads are indistinguishable. Therefore, we have

$$ \begin{align*} |X| = \frac{9!}{4!3!2!} = 1260. \end{align*} $$

So it’s impossible to physically see which arrangements will unique. We said earlier that this is equivalent to having an action by \(D_9\) on the set \(X\). So we just to count the orbits of this action with something called the burnside formula.


Burnside Formula

First, we need the following notation

Action by \(G\) on \(X\)
Given \(g \in G\), let \(\text{Fix}(g) = \{x \in X \ | \ gx = x \} \subseteq X \) be the set of elements fixed by \(g\).


For example \(Fix(e) = X\). Now,

Burnside Formula
If \(G\) acts on a set \(X\), and \(|G| < \infty, |X| < \infty\). Then, the number of orbits is $$ \begin{align*} \frac{1}{|G|}\sum_{g \in G} |\text{Fix}(g)| \end{align*} $$


Example 1

Let’s apply the formula on Example 1. We had \(G = D_4 = \{e,r,r^2,j,rj,r^2j\}\) where \(|G| = 8\) and \(|X| = 6\). For example, take \(r\). We want to know the arrangements that are fixed by \(r\) (the rotation by 90 degrees). What does it mean for an arrangement to be fixed by \(r\). It means that the arrangement when rotated by 90 degrees, it will still be the same arrangement. Observe what happens to the following arrangement.

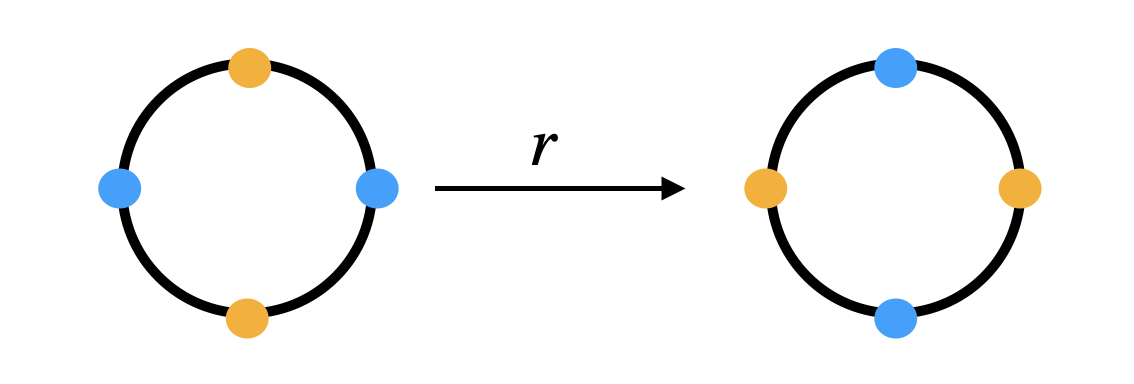
This arrangement is not fixed by \(r\). In fact, all the beads have to have the same color for \(r\) to be able to fix them. So the fix set is zero for \(r\). Note here that \(r^{-1} = r^{3}\) will have the same result for the same reason.

What about \(r^2\) so a rotation by 180 degrees. Observe what happens to the following arrangement

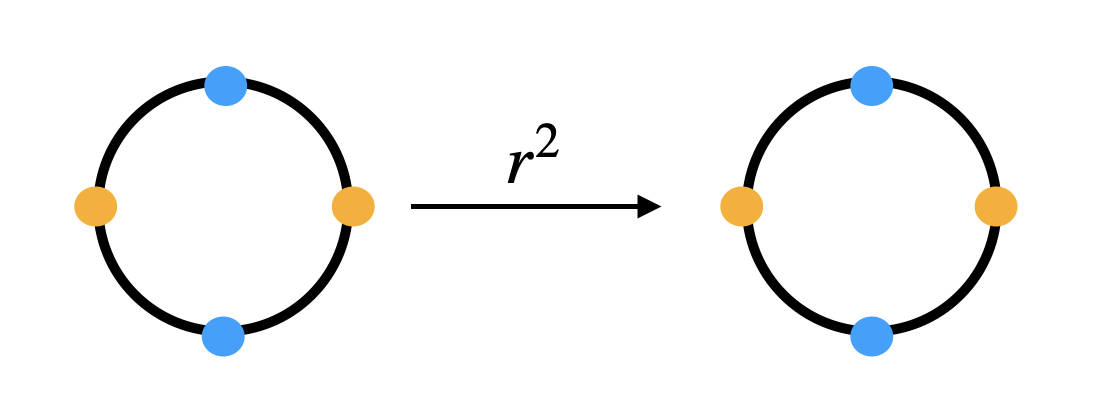
So the beads on the opposite sides have to have the same color for the arrangement to work. We have two arrangements exactly of this kind. So \(|Fix(r^2)| = 2\)

What about \(j\)? Let \(j\) be the flip across the \(x\)-axis. Here, for the arrangement to be fixed, notice that the beads on the axis will not change. So we just need the top and bottom beads to have the same color. The number of arrangements with this condition is 2. In fact, \(r^2j\) (flip around the \(y\)-axis) will have the same number of arrangement fixed.

\(rj\) is a flip around the axis \(x=y\). So the beads on either side of the following axis must have the same color just like following picture

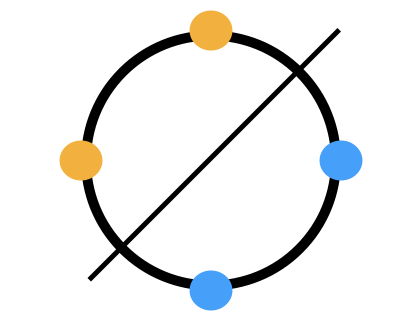
In summary,

\(g\) \(|\text{Fix}(g)|\)
\(e\) 6
\(r, r^3\) 0
\(j, r^2j\) 2
\(rj, r^3j\) 2

So now let’s apply the burnside formula

$$ \begin{align*} \text{number of orbits } &= \frac{1}{|G|}\sum_{g \in G} |\text{Fix}(g)| \\ &= \frac{1}{8}(6+0+2+0+2+2+2+2) \\ &= \frac{16}{8} = 2. \end{align*} $$



Example 2

Here, we had \(G = D_9 = \{e, r, r^2, ..., r^8, j, rj, ..., r^8j\}\). Recall that \(|X| = 1260\). Doing the same analysis

  • \(e\): This is just the entire group so \(|\text{Fix}(e)| = 1260\).
  • \(r\): Like before, we can't fix anything with a 90 degrees rotation. All the beads have to have the same color. This is the same for its inverse \(r^8\).
  • \(r^2\): Note that \(r^2\) has order 9 as well. No possible arrangements here as well. In fact, the same thing happens with \(r^4\) and its inverse \(r^5\).
  • \(r^3\): We have 9 beads. Here we need every third bead to match colors. So like in the following picture

    So vertices 1,4 and 7 have to have the same color. Vertices 2, 5 and 8 have to have the same color. Same for vertices 3, 6 and 9. But we recall that we have 4 red beads, 3 white beads, and 2 yellow beads.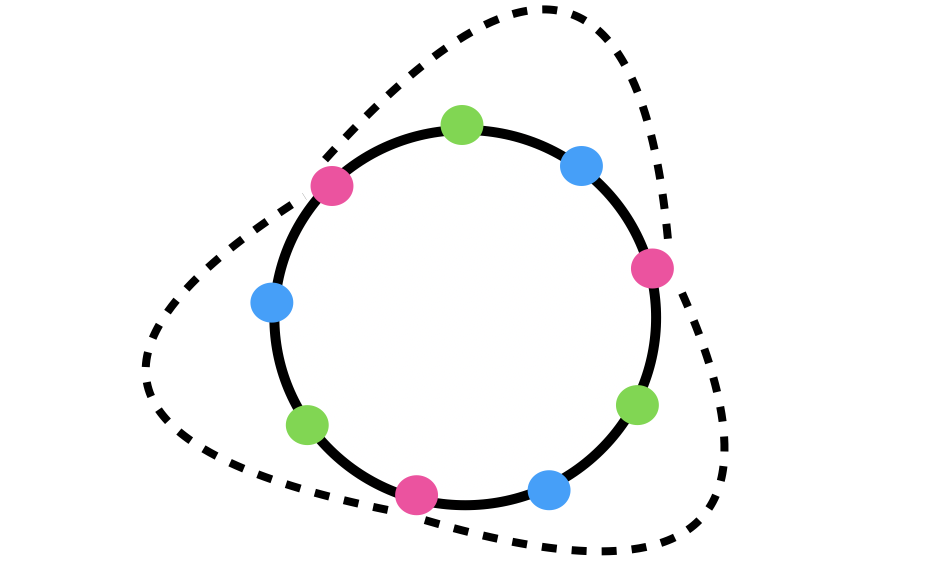
  • \(j\): A flip around the \(x\)-axis. So now there is a black bead fixed by the access itself and the remaining beads must match as follows

    We have 4 red beads, 3 white beads and 2 yellow. So the fixed bead must be a white bead. So now we have the remaining two whites. We need to put one white bead in one of the 4 slots (say in the bottom). We have 4 slots so 4 choices for the second white bead. Next, if we place the yellow bead, we'll have 3 slots available to choose from. Lastly, we have 2 red beads so they must go in the remaining slots. So 12 choices total.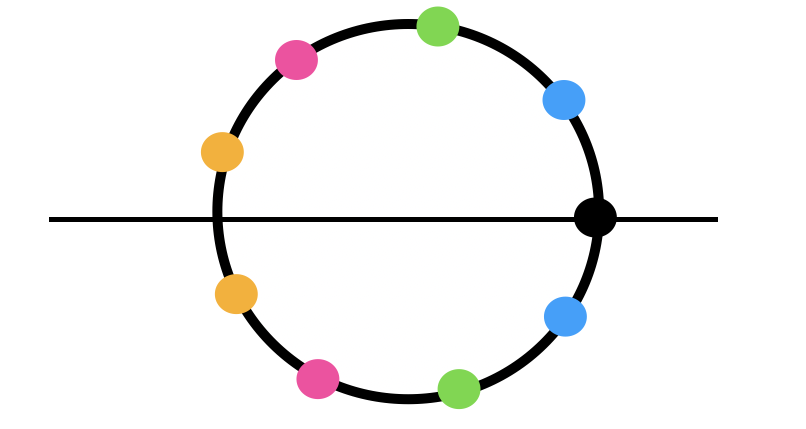


\(g\) \(|\text{Fix}(g)|\)
\(e\) 1260
\(r, r^8\) 0
\(r^2, r^7\) 0
\(r^3, r^6\) 0
\(r^4, r^5\) 0
\(j, r^2j,...,r^8j\) 12

So now let’s apply the burnside formula

$$ \begin{align*} \text{number of orbits } &= \frac{1}{|G|}\sum_{g \in G} |\text{Fix}(g)| \\ &= \frac{1}{18}(1260+9(12)) \\ &= \frac{1374}{18} = 76. \end{align*} $$



Proof of Burnside Formula

Let \(F = \{(g,x) \ | \ g \in G, x \in X, gx = x\}\). (So we’re writing it differently than before but it’s the same. We’re just counting any element that gets fixed by any \(g\). So all of them). We’re going to count this set in two different ways

  1. \(|F| = \sum_{g \in G} | x \in X \ | \ gx = x \} = \sum_{g \in G} |\text{Fix}(g)| \)
  2. \(|F| = \sum_{x \in X} | g \in G \ | \ gx = X \} = \sum_{x \in X} |\text{Stab}(g)| \)

From this, observe that

$$ \begin{align*} \frac{1}{|G|} \sum_{g \in G} |\text{Fix}(g)| &= \frac{1}{|G|} \sum_{x \in X} |\text{Stab}(g)| \\ &= \sum_{x \in X} \frac{|\text{Stab}(g)|}{|G|}. \end{align*} $$

By the Orbit-Stabilizer Theorem, \(|O(x)| = \frac{|G|}{\text{|Stab(x)}|}\). Therefore

$$ \begin{align*} \frac{1}{|G|} \sum_{g \in G} |\text{Fix}(g)| &= \frac{1}{|G|} \sum_{x \in X} |\text{Stab}(g)| \\ &= \sum_{x \in X} \frac{|\text{Stab}(g)|}{|G|} \\ &= \sum_{x \in X} \frac{1}{|O(x)|} \\ &= \sum_{\text{Orbits}} \sum_{x \in O} \frac{1}{|O|} \\ &= \text{number of orbits} \end{align*} $$



Example 3 (Variant of Example 2)

Consider example 2 again. We had a fixed number of beads (4 red, 3 white, 2 yellow). Now, suppose that we don’t have a constraint on the count for each color. We just want a necklace made of 3 colors and 9 beads. Then \(G = D_9\) acts on \(X\) which is the linear arrangements of beads of 3 colors. What is the size of \(X\)? The first bead can be any of the three colors, the second bead can be any of the three colors and so on. So

$$ \begin{align*} |X| = 3^9 = 19,683 \end{align*} $$

Here, we had \(G = D_9 = \{e, r, r^2, ..., r^8, j, rj, ..., r^8j\}\). Recall that \(|X| = 1260\). Doing the same analysis

  • \(e\): This is just the entire group so \(|\text{Fix}(e)| = 1260\).
  • \(r\): Like before, we can't fix anything with a 90 degrees rotation. All the beads have to have the same color. This is the same for its inverse \(r^8\) and as well as \(r^2, r^4, r^5\).
  • \(r^3\): We have 9 beads. Again we need every third bead to have the same color. We have three groups. Each group will need to be of the same color and it can be any color so 3 choices for every group. Therefore, we have \(3^3 = 27\) choices.
  • \(j\): A flip around the \(x\)-axis. Like before, we had a bead fixed on the axis and 4 other groups of two beads each that needed to match colors. Each of these has a choice of 3 colors so \(3^5\) choices.


\(g\) \(|\text{Fix}(g)|\)
\(e\) \(3^9\)
\(r, r^8, r^2, r^4, r^5\) 0
\(r^3, r^6\) \(3^3 = 27\)
\(j, r^2j,...,r^8j\) \(3^5\)

So now let’s apply the burnside formula

$$ \begin{align*} \text{number of orbits } &= \frac{1}{|G|}\sum_{g \in G} |\text{Fix}(g)| \\ &= \frac{1}{18}(3^9 + 6*3 + 2*3^2 + 9*3^5) \\ &= \frac{1374}{18} = 1219. \end{align*} $$




References