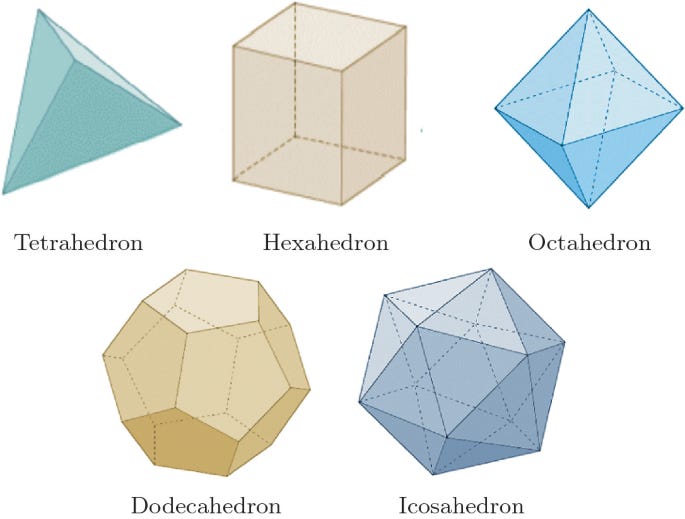
A regular polyhedra is a three dimensional solid where the faces are congruent regular polygons and such that the same number of faces meet at each vertex. There are exactly 5 regular polyhedra described below:

Vertices Edges Faces Vertices on the Faces Edges at a Vertex \(|G|\)
Tetrahedron 4 6 4 3 3 12
Cube 8 12 6 4 3 24
Octahedron 6 12 8 3 4 24
Dodecahedron 20 30 12 5 3 60
Icosahedron 12 30 20 3 5 60



Symmetry Groups

The reason we introduced these regular polyhedra is because we want to study their symmetry groups. So now, given a Polyhedron, we have a set \(V\) of vertices (with the center of mass at 0). Define, the symmetry group \(G\) of the polyhedron as

$$ \begin{align*} G = \{ A \in SO(3) \ | \ v \in V \Leftrightarrow Av \in V, v \in \mathbf{R}^3 \} \end{align*} $$

So this a point is a vertex if and only if, rotating this point by \(A\) is also a vertex. It should be clear that \(G\) is a subgroup of \(SO(3)\). For example, how many rotational symmetries does the cube have? It is twice the number of edges for all of them. In fact, the symmetry group of the octahedron and the cube are isomorphic to each other because the two solids are duel of each other. Similarly, the symmetry group of dodecahedron is isomorphic to the symmetry group of the icosahedron.


The Symmetry Group of the Tetrahedron

Let’s study the specific symmetry group of the Tetrahedron. Notice that if we draw a line from any vertex through the centroid of the opposite face, we get an axis where we can rotate around. We have two possible rotations here. Going one third clockwise and one third of full rotation counter clockwise. So \(2\pi / 3\) in either direction. Each of these have order 3. Moreover, there are 4 possible axes of this type since we have 4 different vertices.

The next possible rotational symmetry is the one that goes through a mid point of an edge to another midpoint of another edge. It’s a 180 degrees symmetry. So its order is 2 and we have 3 such possible axes.

Axis of Rotation Angle of Rotation Order of Symmetry # of Axes # of Symmetries of This Type Cycle Type
Vertex/Centroid (1) \(\frac{+2\pi}{3}\) 3 4 4 3-cycle
Vertex/Centroid (2) \(\frac{+2\pi}{3}\) 3 4 4 3-cycle
Edge Midpoint to Midpoint \(\frac{2\pi}{2}\) 2 3 3 2+2 cycle type
Identity Rotation

So we have exactly 12 symmetries of the tetrahedron. This group is isomorphic to \(A_4\). The group of even permutations inside \(S_4\). How does this happen? Consider the set of vertices \(\{v_1,v_2,v_3,v_4\}\) of a tetrahedron. Now, any symmetry permutes the vertices. Since we have 4 vertices, then \(Sym(4) \cong S_4\). We can construct a homomorphism such that

$$ \begin{align*} \phi: G \rightarrow Sym(V) \cong S_4 \\ \end{align*} $$

The kernel of this homomorphism is just the identity symmetry. If you think about it, what symmetry corresponds to the identity permutation? it’s just the identity symmetry so the kernel is the trivial kernel. How do we find the actual permutations that get mapped to the symmetries in the above table. Well, the first kind where the axis is from a vertex to the centroid of a face is equivalent to a permutation that leaves one vertex fixed. Thus, we get all the 3-cycle type permutations. For the other edge to edge axis kind of symmetry, notice here that each pair of vertices switch, therefore, we have to include the 2+2 cycle type permutations. Therefore, the the permutations we have are the 2+2 and the 3-cycle permutations. There are 12 of those and in fact, this is the subgroup \(A_4\). Since the kernel of \(\phi\) is the trivial subgroup, then \(G \cong A_4\).


The Symmetry Group of the Cube

Next, we want to explore the symmetries of the cube. The first symmetry that we can construct is the symmetry around the axis that goes between two opposite vertices. We have 8 vertices total. Therefore, there are 4 pairs of those vertices. So 4 axes total. A rotation is one third of a full spin, so the angle is \(2\pi/3\). Since we have two choices for the angle, then the number of total rotations is \(2*4 = 8\) total rotations.

The next symmetry is the symmetry around the axis connecting the midpoints of two opposite edges. We have 12 edges. So we have 6 pairs of opposite edges. The angle is exactly 180 degrees. So we have exactly 6 symmetries

The next symmetry is the symmetry around the axis connecting the centroid of two faces. We can rotate by a 90 degrees either clockwise or counter clockwise. There are 6 faces so 3 opposite pairs of faces. There are 2 rotations for each pair so a total of 6 symmetries. But we can also rotate by 180 degrees. So therefore we have another 3 rotations here.

Axis (Cube) # of Axes Angle of Rotation Order of Symmetry # of Symmetries of This Type Axis (Octahedron) Cycle Type
Vertex/Vertex 4 \(\pm \frac{2\pi}{3}\) 3 8 Faces/Face 3-cycle
Edge/Edge 6 \(\frac{2\pi}{2}\) 2 6 Edge/Edge 2-cycle
Face/Face 3 \(\pm \frac{2\pi}{4}\) 4 6 Vertex/Vertex 4-cycle
Face/Face 3 \(\frac{2\pi}{2}\) 2 3 2+2
Identity Rotation 1 1 e

So we have exactly 24 symmetries just like we expected (twice the number of edges). What group is this isomorphic to? It turns out to be isomorphic to \(S_4\). Previously we have 4 vertices so it was easy to see or construct the homomorphism. But now we have 8 vertices so it’s not exactly clear. We want to construct a homomorphism from \(G\) to \(S_4\). So we need to find function from \(G\) to \(Sym(\text{4 things in a cube})\). What will the 4 things be? The easiest choice is the diagonals. We have 4 different diagonals between every pair of opposite vertices. The symmetry of the cube permutes the 4 diagonals.

So next we want \(\phi\) to not just be a homomorphism. We want it to be an isomorphism. Each group has exactly 24 elements. So if we should that \(\phi\) is injective, then that suffies to conclude that it’s an isomorphism. In order to do that, we just need to figure out what each of these symmetries do. So

  • Vertex/Vertex Symmetry: Notice here that the diagonal between the axis we're rotating around is fixed. While the other three diagonals get permuted. The other three diagonals get permuted cyclicly. So this is 3-cycle permutation.
  • Edge/Edge Symmetry: Here the axis is from an edge midpoint to another edge point. When we rotate around this axis by 180 degrees, notice here that two of the diagonals stay fixed. The ones in the xy plane. The remaining diagonals get switched. So this is a two cycle.
  • Face/Face Symmetry (Quarter Turn): When we do a quarter turn here, all the diagonals get switched cyclicly so this is a 4-cycle.



The Symmetry Group of the Dodecahedron

Next, we’ll do the symmetry group of the Dodecahedron

  • Vertex/Vertex Symmetry: We have a total of 20 vertices. So 20 pairs of axes. Each vertex is connected to three edges. So each turn is a third of a full turn like before. Since it's 3 turns total, then each symmetry is of order 3. The number of symmetries is then 10*2 for each angle, so 20 total symmetries.
  • Edge/Edge Symmetry: Here the axis is from an edge midpoint to another edge point. Since an edge needs to go to another edge, the only angle here is 180 degrees. So the order is 2. There are 30 edges so we have 15 pairs.
  • Face/Face Symmetry: We have 12 faces total. When we rotate around an axis connecting two faces, then there are 4 possible turns. So the angle is \(\pm \frac{2\pi}{3}\). Therefore, the order is 5.
Axis (Dodecahedron) # of Axes Angle Order of \(g\) # of \(g\) Axis (Icosahedron) Cycle Type
Vertex/Vertex 10 \(\pm \frac{2\pi}{3}\) 3 20 3-cycle
Edge/Edge 15 \(\pm \frac{2\pi}{2}\) 2 15 2+2
Face/Face 6 \(\pm \frac{2\pi}{5}\) 5 12 5-cycle
Face/Face 6 \(\pm \frac{4\pi}{5}\) 5 12 5-cycle
Identity Rotation 1 1 e

So there are 60 total symmetries matching the rule (edges * 2). Note here that all the cycles are even cycles. In fact, \(G\) is isomorphic to \(A_5\). To show this we need to construct a homomorphism to a permutation group of a set of 5 things in the dodecahedron such that

$$ \begin{align*} G \rightarrow Sym(\text{5 things in the dodecahedron}) \cong S_5 \end{align*} $$

Take the 30 edges and divide them into groups of 6 edges each. Each edge has 5 other friends. One friend is the opposite edge that’s parallel to it. And there are 4 other perpendicular edges to it. So everything in group of 6 is either parallel or perpendicular.

The image of this homomorphism is exactly \(A_5\) and this homomorphism is also injective. From these two facts, we can conclude that \(G \rightarrow A_5\). To show this, we simply determine the cycle type like we did before in the above table (last column). This is really hard to visualize actually. But you want to see what happens to the group of edge friends when we rotate around each of the axes in the above table. For example, for the face to face axis, all the friends get cyclically rotated. So it’s a 5-cycle.



References