We previously proved the uniqueness of an elementary divisor decomposition. Today, we want to prove the existence of the elementary divisor decomposition. To do this, we will show instead the existence of the invariant factor decomposition. But when we show this, it turns out that it implies something for a larger class than just finite abelian groups. It’s going to imply this any finitely generated abelian groups.

Definition
A group \(G\) is finitely generated if \(G = \langle S \rangle\) where \(S\) is a finite subset of \(G\), \(S \subseteq G\)


Examples:

  • For example, every cyclic is finitely generated by this definition (by a subset of one element). An example is \(\mathbf{Z}\). It is infinite but it is finitely generated by an element.
  • Every finite group \(G\) is finitely generated. \(G = \langle G \rangle\).
  • \(D_{\infty} = \langle r, j \rangle\)
  • \((\mathbf{Q},+)\), the group of rational numbers with addition is not finitely generated.

We also have the following fact

Proposition
If \(G \cong H\), \(G\) is finitely generated if and only if \(H\) is finitely generated.


So being finitely generated is isomorphism invariant. What we want to prove is the following

Proposition
If \(G\) is finitely generated and abelian, then $$ \begin{align*} G \cong \mathbf{Z}/\mathbf{Z}_{d_1} \times \mathbf{Z}/\mathbf{Z}_{d_2} \times ... \times \mathbf{Z}/\mathbf{Z}_{d_k} \end{align*} $$ For some \(d_1,...,d_k \geq 0, k \geq 0, d_i \ | \ d_{i+1}\)


Example: Suppose \(G\) has \(d_i = 1,3,12,12,720,0,0\) Then

$$ \begin{align*} G &\cong \mathbf{Z}/\mathbf{Z}_{1} \times \mathbf{Z}/\mathbf{Z}_{3} \times \mathbf{Z}/\mathbf{Z}_{12} \times \mathbf{Z}/\mathbf{Z}_{12} \times \mathbf{Z}/\mathbf{Z}_{720} \times \mathbf{Z}/\mathbf{Z}_{0} \times \mathbf{Z}/\mathbf{Z}_{0} \\ &\cong \mathbf{Z}/\mathbf{Z}_{3} \times \mathbf{Z}/\mathbf{Z}_{12} \times \mathbf{Z}/\mathbf{Z}_{12} \times \mathbf{Z}/\mathbf{Z}_{720} \times \mathbf{Z} \times \mathbf{Z} \\ &\cong \mathbf{Z}/\mathbf{Z}_{3} \times \mathbf{Z}/\mathbf{Z}_{12} \times \mathbf{Z}/\mathbf{Z}_{12} \times \mathbf{Z}/\mathbf{Z}_{720} \times \mathbf{Z}^2 \end{align*} $$

For finite abelian groups, we won’t have terms like \(\mathbf{Z}\) since they are finite. So we will get exactly the invariant factor form out of this. So this proposition will essentially give us the existence of invariant factor decomposition. It will take this lecture and probably the next lecture to prove it.


The Existence of Invariant Factor Decomposition Proof Sketch

So now we want to describe the steps involved in this proof:

  1. If \(G\) is finitely generated and abelian, then we will see that
    $$ \begin{align*} G &\cong \mathbf{Z}^m/N \text{ where } \mathbf{Z}^m = \mathbf{Z} \times ... \times \mathbf{Z} \end{align*} $$
    In fact, what we will really show is that there exists a surjective homomorphism such that
    $$ \begin{align*} \phi: \mathbf{Z}^m \rightarrow G \end{align*} $$
    So now since we have a surjective homomorphism, we can then use the isomorphism theorem to conclude that
    $$ \begin{align*} G \cong \mathbf{Z}^m / (N = ker(\phi)) \end{align*} $$
  2. What is \(N\) going to be? To answer this, we want to study the subgroups of \(\mathbf{Z}^m\). We will show that every subgroup of \(\mathbf{Z}^m\) is finitely generated (won't be easy) and abelian. As a consequence, we will get that there exists a surjective homomorphism such that
    $$ \begin{align*} \mathbf{Z}^n \xrightarrow{\rho} N \xrightarrow{i} \mathbf{Z}^m \end{align*} $$
    From this we can form the composite homomorphism \(\alpha = i \circ \rho\) between \(\mathbf{Z}^n\) and \(\mathbf{Z}^m\).
    Notice above that the subgroup \(N\) must be the image of \(\alpha\) so \(N = \alpha(\mathbf{Z}^n)\). So, now we can re-write what we have to be
    $$ \begin{align*} G \cong \mathbf{Z}^m / \alpha(\mathbf{Z}^n) \end{align*} $$
    For some homomorphism \(\alpha: \mathbf{Z}^n \rightarrow \mathbf{Z}^m\). We still don't know what \(\alpha\) is but now the question of understanding finitely generated abelian can be reduced to a question of understanding homomorphisms.
  3. Every homomorphism \(\alpha: \mathbf{Z}^n \rightarrow \mathbf{Z}^m\) is of the form
    $$ \begin{align*} L_A: \ &\mathbf{Z}^n \rightarrow \mathbf{Z}^m \\ &L_A(x) = Ax \end{align*} $$
    where \(A \in \text{Mat}_{m \times n}(\mathbf{Z})\) and \(x = [x_1 \ x_2 \ ... \ x_n]^T \in \mathbf{Z}_n, x_i \in \mathbf{Z} \).
    So any homomorphism from \(\mathbf{Z}^n \rightarrow \mathbf{Z}^m\) can be written as a left multiplication by a matrix \(A\). So now we can write
    $$ \begin{align*} G \cong \mathbf{Z}^m / L_A(\mathbf{Z}^n) \end{align*} $$
    So we're reducing the problem to linear algebra over the integers.
  4. Say \(P \in \text{Mat}_{n \times n}(\mathbf{Z})\) is integer invertible if \(P^{-1}\) exists and \(P^{-1} \in Mat_{n \times n}(\mathbf{Z}) \).
    Then, if \(B = PAQ\), where \(P, Q\) are integer invertible, then
    $$ \begin{align*} G \cong \mathbf{Z}^m / L_A(\mathbf{Z}^n) \cong \mathbf{Z}^m / L_B(\mathbf{Z}^n) \end{align*} $$
    The goal is that if we didn't want \(A\) or \(A\) wasn't in the right form, we can put it in standard form (smith normal form) and use a matrix that we want.
  5. A matrix \(D \in \text{Mat}_{m \times n}(\mathbf{Z})\) is a Smith normal form if
    $$ \begin{align*} D = \begin{pmatrix} d_1 & 0 & \cdots & 0 & 0 \\ 0 & d_2 & \ddots & \ddots & 0 \\ 0 & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & d_s & 0 \\ \end{pmatrix} \end{align*} $$
    where \(d_i \geq 0\) and \(d_i \ | \ d_{i+1}\). Since, it doesn't need to be a square matrix, then the last column(s) might just be zero.
    If we have this, then the claim is that
    $$ \begin{align*} \mathbf{Z}^m / L_D(\mathbf{Z}^n) \cong \mathbf{Z}/\mathbf{Z}_{d_1} \times \mathbf{Z}/\mathbf{Z}_{d_2} \times ... \times \mathbf{Z}/\mathbf{Z}_{d_s} \times \mathbf{Z}^{m-s} \end{align*} $$
  6. For every \(A \in \text{Mat}_{n \times n}(\mathbf{Z})\) there exists a integer invertible \(P, Q\), such that \(D = PAQ\) is a Smith normal form. This implies that
    $$ \begin{align*} G \cong \mathbf{Z}^m / L_A(\mathbf{Z}^n) \cong \mathbf{Z}^m / L_D(\mathbf{Z}^n) \end{align*} $$

So what we did here is that we turned the problem into a problem about quotients by the image of a homomorphism that looked liked a left multiplication by a matrix. And then we took this matrix and put it in a Smith normal form. This leads to the form we want.


Using Addition instead of Multiplication for the Proof

We have an abelian group \(G\). The standard so far has been writing the group with multiplication but since we’re going to turn to linear algebra, we’re going to switch to addition.

multiplicative additive
\(ab\) \(a+b\)
\(e\) \(0\)
\(a^{-1}\) \(-a\)
\(n \in \mathbf{Z}, a \in G\) \(a^{n}\) \(na\)
\(n_i \in \mathbf{Z}, a_i \in G\) \(a^{n_1}_1a^{n_2}_2...a^{n_k}_k\) \(n_1a_1 + n_2a_2 + ... + n_ka_k\)
\(N \subseteq G\) \(aN\) \(a + N\)



Proof Setup: Definitions

Before starting with the proof, we need some setup, starting with this definition.

Definition
If \(G\) is an abelian group with addition. A subset \(S \subseteq G\) is linearly independent if \(\forall \ a_1,...,a_n \in S\) and \(\forall \ c_1,...,c_n \in \mathbf{Z}\), If $$ \begin{align*} c_1a_1 + ... + c_na_n = 0 \end{align*} $$ then, \(c_1 = ... =c_n = 0\).


In Vector Spaces, the \(c_i\)s are scalars.

Example: Suppose \(S \subseteq G\) and \(S = \{a\}\). What does it mean for \(S\) to be linearly independent?
From the definition, \(S\) is linearly indenpendent if

$$ \begin{align*} \forall c \in \mathbf{Z}, \quad ca = 0 \end{align*} $$

Then this implies that \(c = 0\). So no matter what \(c\) is if \(ca = 0\) only implies that \(c = 0\). So \(a\) must have infinite order (\(o(a) = \infty\)). This isn’t the same for subsets with more than 1 element.
We also have the notion of a basis

Definition
A basis \(B\) of \(G\) is a subset \(B \subseteq G\) which is linearly independent and generates \(G\) $$ \begin{align*} G = \langle B \rangle = \mathbf{Z}B = \{ c_1x_1 + ... + c_nx_n \ | \ c_i \in \mathbf{Z}, x_i \in B \} \end{align*} $$


Example 1: \(\{1\}\) is a basis for \(\mathbf{Z}\)

Example 2: \(\mathbf{Z}_n\) has no basis. Why? we can’t have non-empty linear independent. Because if we have a non-empty subset with only element, this element will have infinite order.

So unlike Vector Space, not every abelian group will have a basis

Definition
\(G\) is a free abelian group if it is abelian and there exists a basis.


Example 1: \(G = Q^{\times}/\{\pm 1\}\) with multiplication is a free abelian group. It has an infinite basis

$$ \begin{align*} B = \{\{\pm p\} \ | \ p \text{ is prime} \} \end{align*} $$

Because every non-zero rational can be written uniquely as a product of prime powers.

$$ \begin{align*} q = \pm p_1^{k_1}...p_r^{k_r} \quad \text{ where } k_i \in \mathbf{Z} \end{align*} $$


Example 2: Suppose \(G = (\mathbf{Z}^n, +)\). Let \(e_k = (0,0,..1,..,0,0)\) be the standard basis vector where the \(k\)th entry is 1. Then the set

$$ \begin{align*} B = \{e_1,e_2,...,e_n\} \end{align*} $$

is a basis for \(\mathbf{Z}^n\). Any element in \(\mathbf{Z}^n\) can be written a linear combination of the standard elements

$$ \begin{align*} (c_1,c_2,...,c_n) = c_1e_1+...+c_ne_n \quad \text{ where } c_i \in \mathbf{Z} \end{align*} $$



Proof Setup: Propositions

So we have the steps and we have the definitions that we need. We also need the following proposition

Proposition
If \(G\) is abelian and let \(a_1,...,a_n\) be a list of elements in \(G\). Then there exists a homomorphism $$ \begin{align*} \phi: \mathbf{Z}^n &\longrightarrow G \\ \phi(c_1,...,c_n) &= c_1a_1 + ... + c_na_n \quad \text{ where } c_i \in \mathbf{Z} \end{align*} $$ \(\phi\) is injective if and only if \(a_1,...a_n\) are linearly independent.
\(\phi\) is surjective if and only if \(a_1,...a_n\) generates \(G\).


To show it’s injective, we need to check the kernel of \(\phi\). To show subjectivity, we need to check the image of \(\phi\). [Exercise]. As a consequence we get the following corollary

Proposition
If \(G\) is a free abelian group with a basis \(B\) where \(|B| = n < \infty\), then \(G \cong \mathbf{Z}^n\).


Another consequence (the one we care about)

Proposition
If \(G\) is a finitely generated and abelian, there exists a surjective homomorphism \(\phi: \mathbf{Z}^n \longrightarrow G\).





Subgroups of Finitely Generated Groups

[Lecture 24]. So given a finitely generated group \(G = \langle a_1,...,a_n \rangle\). We want to know is this property of being finitely generated inherited? Do subgroups and quotient groups of \(G\) are also finitely generated? If we have a normal subgroup \(N\). Is \(G/N\) finitely generated? The answer is actually yes. In fact, can write \(G/N = \langle a_1N,...a_nN \rangle\). So quotients of finitely generated groups are finitely generated as well.

One thing to note here is that one of these elements will turn out to be the identity element and since it’s the identity, then we don’t need to keep it in the generators list. So \(G/N = \langle a_1N_1,...a_{n-1}N \rangle\). We can throw one of the elements out. (explain more?)

A related question to this. If we have a subgroup \(H \leq G\) where \(G\) is finitely generated. Is \(H\) finitely generated? The answer is actually no. It doesn’t need to be. In fact, only if \(G\) is finitely generated and abelian, then every subgroup \(H \leq G\) is also finitely generated. We will prove this but to do so, we’ll prove the following required lemma first.

Lemma
Let \(H\) be an (abelian) group and let \(N\) be a normal subgroup of \(H\) (\(N\) is always normal since \(H\) is abelian). If \(N\) and \(H/N\) are finitely generated, then \(H\) is finitely generated.


Note here that this lemma in fact works for all groups with a normal subgroup and not just abelian groups but right now we only care about the abelian case and it will also make the proof easier.

Proof
Suppose \(N\) is a normal subgroup of \(H\) and suppose that both \(N\) and \(H/N\) are finitely generated. Then, we can write

$$ \begin{align*} N &= \mathbf{Z}\{x_1,...,x_m\} \\ H/N &= \mathbf{Z}\{\bar{y_1},...,\bar{y_n}\} \end{align*} $$

Now, for each \(\bar{y_i}\), pick \(y_i \in H\) such that \(\bar{y_i} = y_i + N\). So \(y_i\) is the representative for this coset. Another way to think about this is to remember that we have the quotient homomorphism \(\pi\) where

$$ \begin{align*} \pi: H &\longrightarrow H/N \\ \pi(y_i) &= \bar{y_i} \end{align*} $$

Given this, we claim that \(H\) is generated by \(\mathbf{Z}\{x_1,...,x_m,y_1,...,y_n\}\). So we’re combining the elements of \(N\) and all the representatives of the cosets. This gives us a generating set for \(H\) itself. To see why it’s true. Suppose that \(u \in H\). The goal is to write \(u\) in terms of the elements in our claim. Consider the image of \(u\) under \(\pi\). Its image is in the quotient group \(H/N\) so we can write

$$ \begin{align*} v = \pi(u) = b_1\bar{y_1} + ... + b_n\bar{y_n} \in H/N \quad \text{ for some } b_i \in \mathbf{Z} \end{align*} $$

We can do this because the set \(\{\bar{y_1},...,\bar{y_n}\}\) generates \(H/N\). So we can write \(v\) as a linear combination of the elements in the set like we did. Now define \(\hat{v}\) to be an element in \(H\). We can also write it

$$ \begin{align*} \hat{v} = b_1y_1 + ... + b_ny_n \in H \end{align*} $$

We can do this because each \(y_i\) is in \(H\) and \(H\) is closed so \(\hat{v}\) is in \(H\). Observe that \(\pi(\hat{v}) = v\) because we defined earlier that \(\pi(y_i) = \bar{y_i}\). So now we have

$$ \begin{align*} \pi(u) &= v = \pi(\hat{v}) \end{align*} $$

So now calculate \(\pi(u - \hat{v})\), we will see that

$$ \begin{align*} \pi(u - \hat{v}) &= v - v = 0 \end{align*} $$

This means that \(u - \hat{v}\) is in the kernel of \(\pi\) which means that \(u - \hat{v} \in N\). But \(N\) is finitely generated so we can express \(u - \hat{v}\) in terms of the elements in \(N\) so

$$ \begin{align*} u - \hat{v} = a_1x_1 + ... + a_nx_n \in N \text{ where } a_i \in \mathbf{Z} \\ u = (a_1x_1 + ... + a_nx_n) + (b_1y_1 + ... + b_ny_n) \end{align*} $$

So this says that any element in \(H\) can be written interms of those factors which means that \(H\) is finitely generated. \(\ \blacksquare\)

Now we’re ready to prove the main theorem

Theorem
If \(G\) is finitely generated and abelian, then every subgroup \(H \leq G\) is also finitely generated.


Proof
Let \(G = \mathbf{Z}\{a_1,...,a_n\}\) and \(H \leq G\). We want to show that \(H\) is finitely generated. We will show this by induction on the size of generating set.

Base Case:
If \(n = 0\), then \(G = \mathbf{Z}\{\} = \{e\}\). So \(G\) is the trivial group.
If \(n = 1\), then, \(G = \mathbf{Z}\{a\}\). So \(G\) is cyclic. Any subgroup of a cyclic group is cyclic.

Inductive Case: \((n \geq 2)\). Let \(a_n = a\) in the generators list just to make it easy to read.
First, since \(G\) is abelian, then all of \(G\)’s subgroups are normal. Consider the subgroup generated by the last element in the list of generators in \(G\). So \(\mathbf{Z}\{a\}\). This subgroup is normal. Now, consider the intersection of \(H\) and \(\mathbf{Z}\{a\}\). This is also a subgroup of both \(\mathbf{Z}\{a\}\) and \(H\) by the Diamond Isomorphism Theorem. In fact, we will get the following diagram.

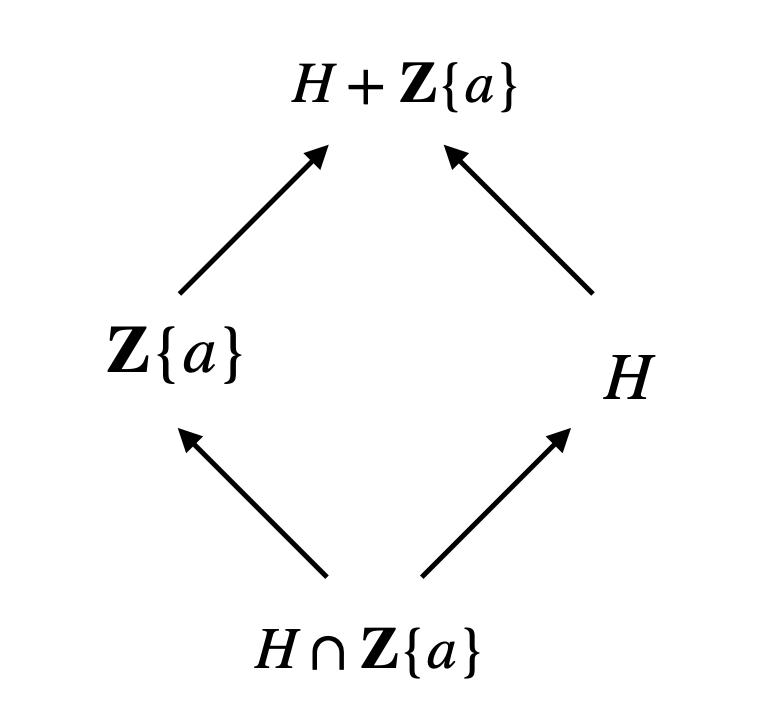
Now, let the intersection \(H \cap \mathbf{Z}\{a\}\) be \(N\). We will take the quotient group \(H/N\). Similarly, we have another quotient group \(H + \mathbf{Z}\{a\}/\mathbf{Z}\{a\}\). These two quotient groups are isomorphic by the Diamond Isomorphism Theorem.

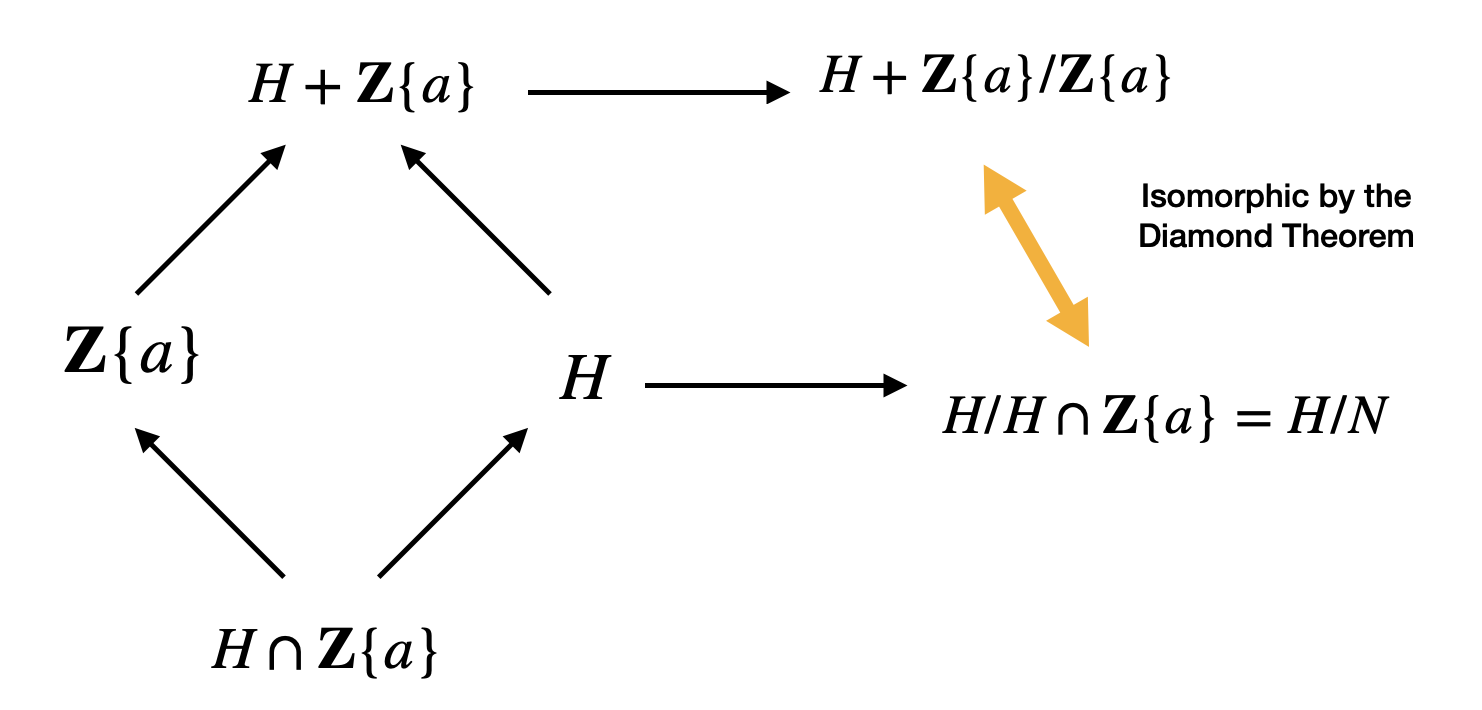
Next, take the quotient group \(G/\mathbf{Z}\{a\}\). Notice here that \(H + \mathbf{Z}\) is a subgroup of \(G\) and that we’re taking the quotient by the same subgroup \(\mathbf{Z}\{a\}\). Therefore, by the correspondance theorem, we will see that \(H + \mathbf{Z}\{a\}/\mathbf{Z}\{a\}\) is a subgroup of \(G/\mathbf{Z}\{a\}\).

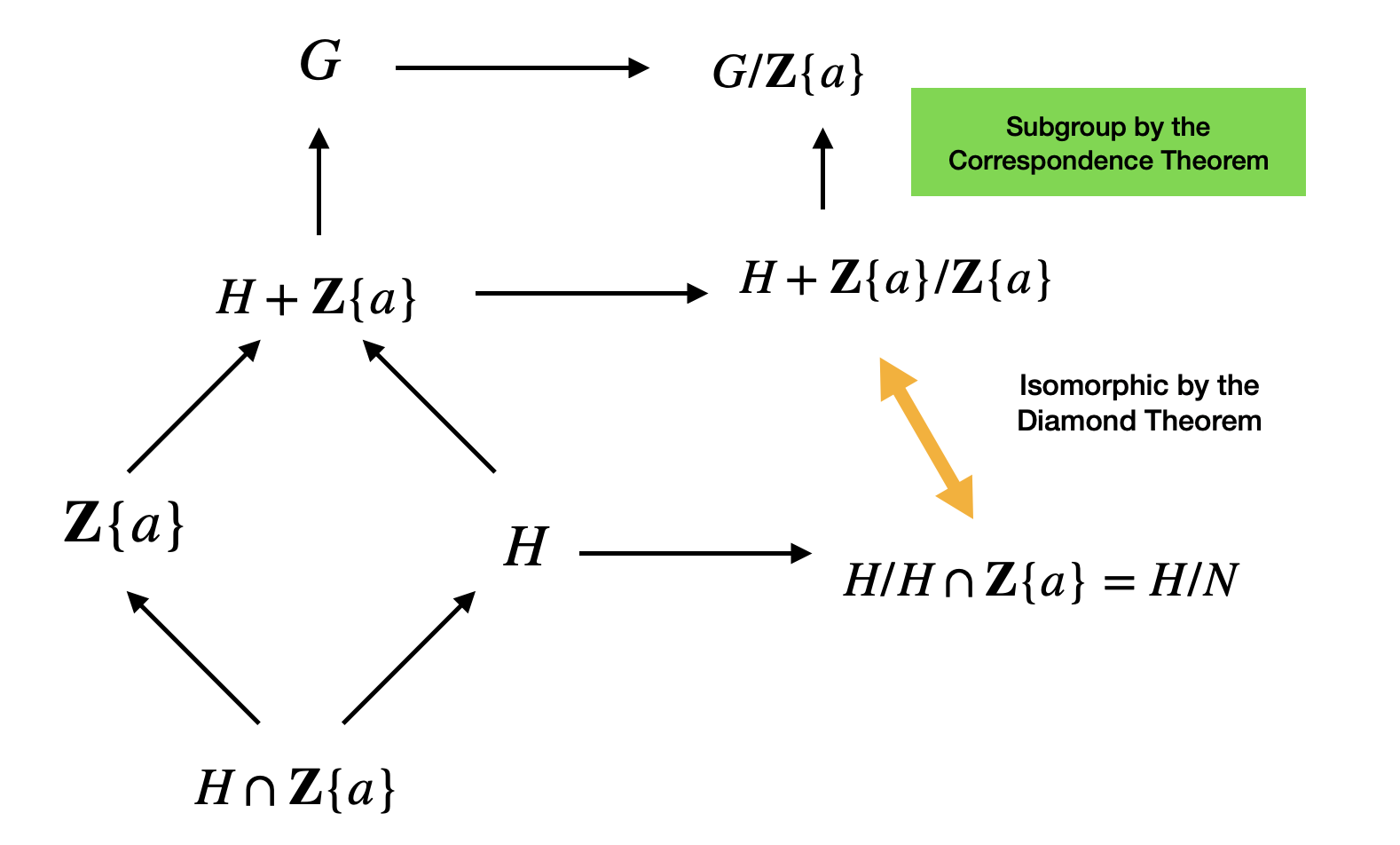
So now, observe that \(G\) is generated by \(n\) elements. The group \(G/\mathbf{Z}\{a\}\) is generated by \(n-1\) elements. Why? Recall that we said earlier that since the subgroup has one element \(a\) from the generators, then this element will be come the identity element in the quotient group and we don’t need to include it in the list of generators for the quotient group.

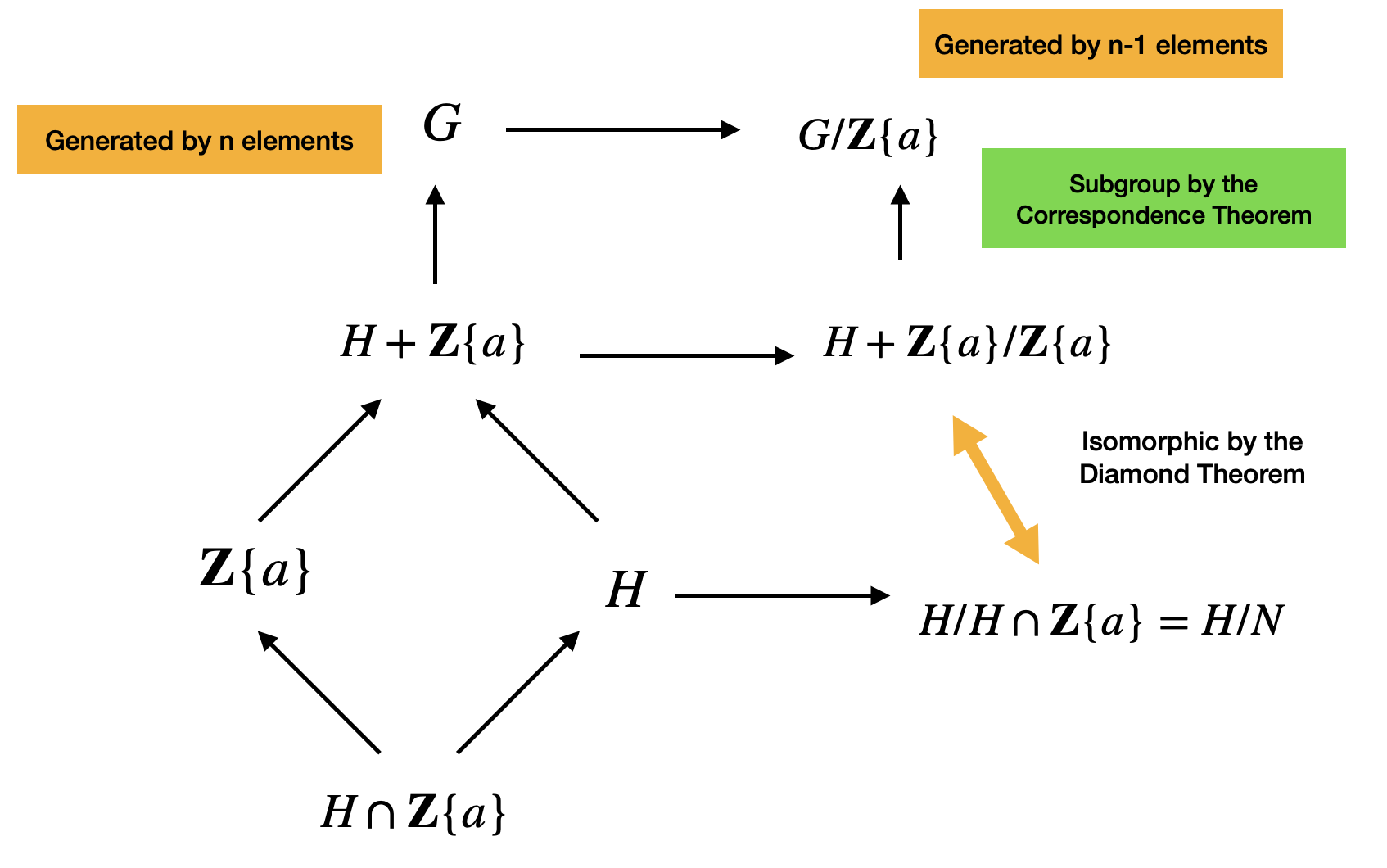
Also note, that \(\mathbf{Z}\{a\}\) is a subgroup generated by one element so it’s cyclic and so it’s finitely generated. Since the intersection \(N = \mathbf{Z}\{a\}\) is a subgroup of \(\mathbf{Z}\{a\}\), then it’s also cyclic and finitely generated.

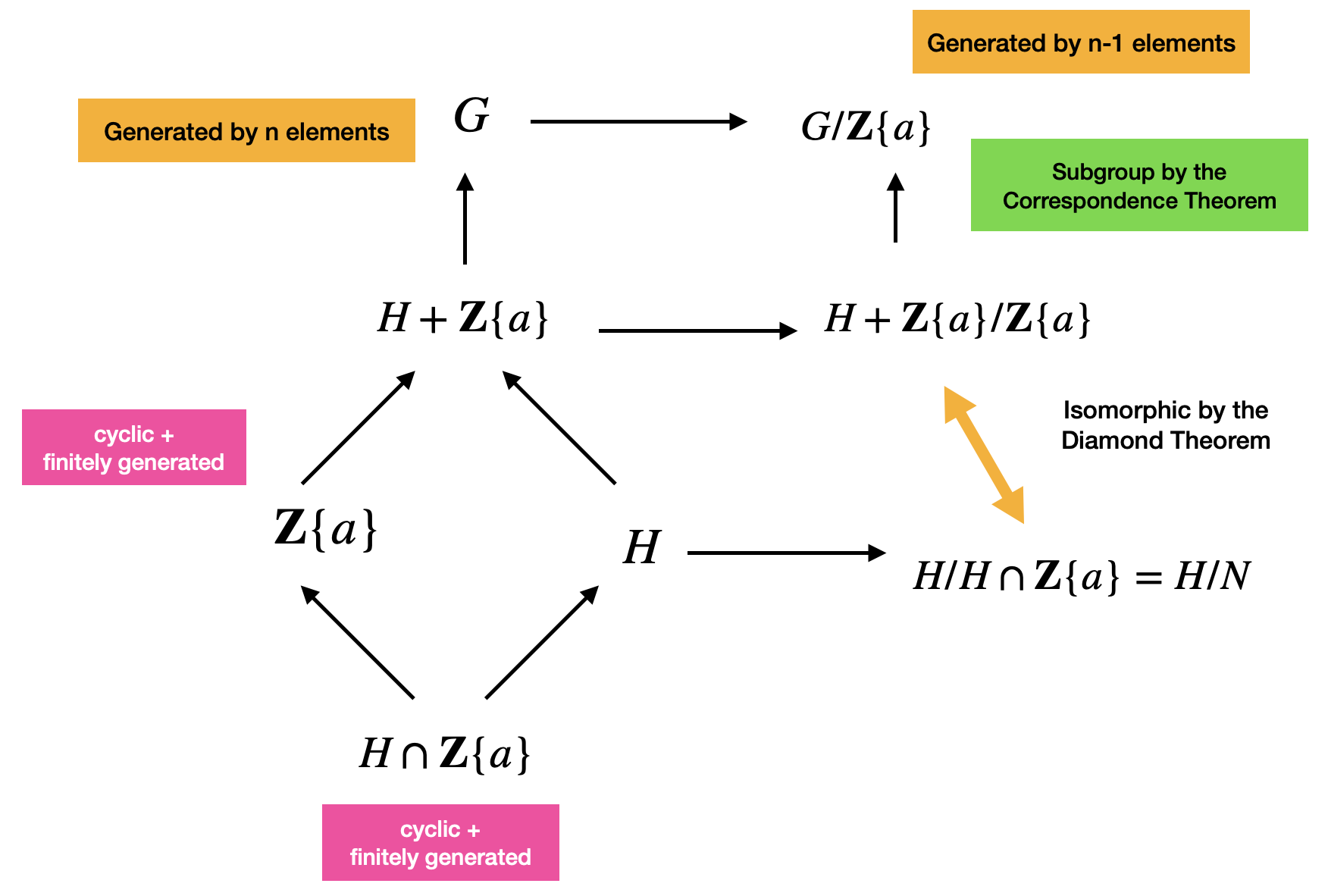
We can now use the induction hypothesis to say that since \(G/\mathbf{Z}\{a\}\) is generated by \(n-1\) elements, then all its subgroups are also finitely generated. So \(H + \mathbf{Z}\{a\}/\mathbf{Z}\{a\}\) is finitely generated. But this group is isomorphic to \(H/H \cap \mathbf{Z}\{a\} = H/N\). So \(H/N\) is also finitely generated.

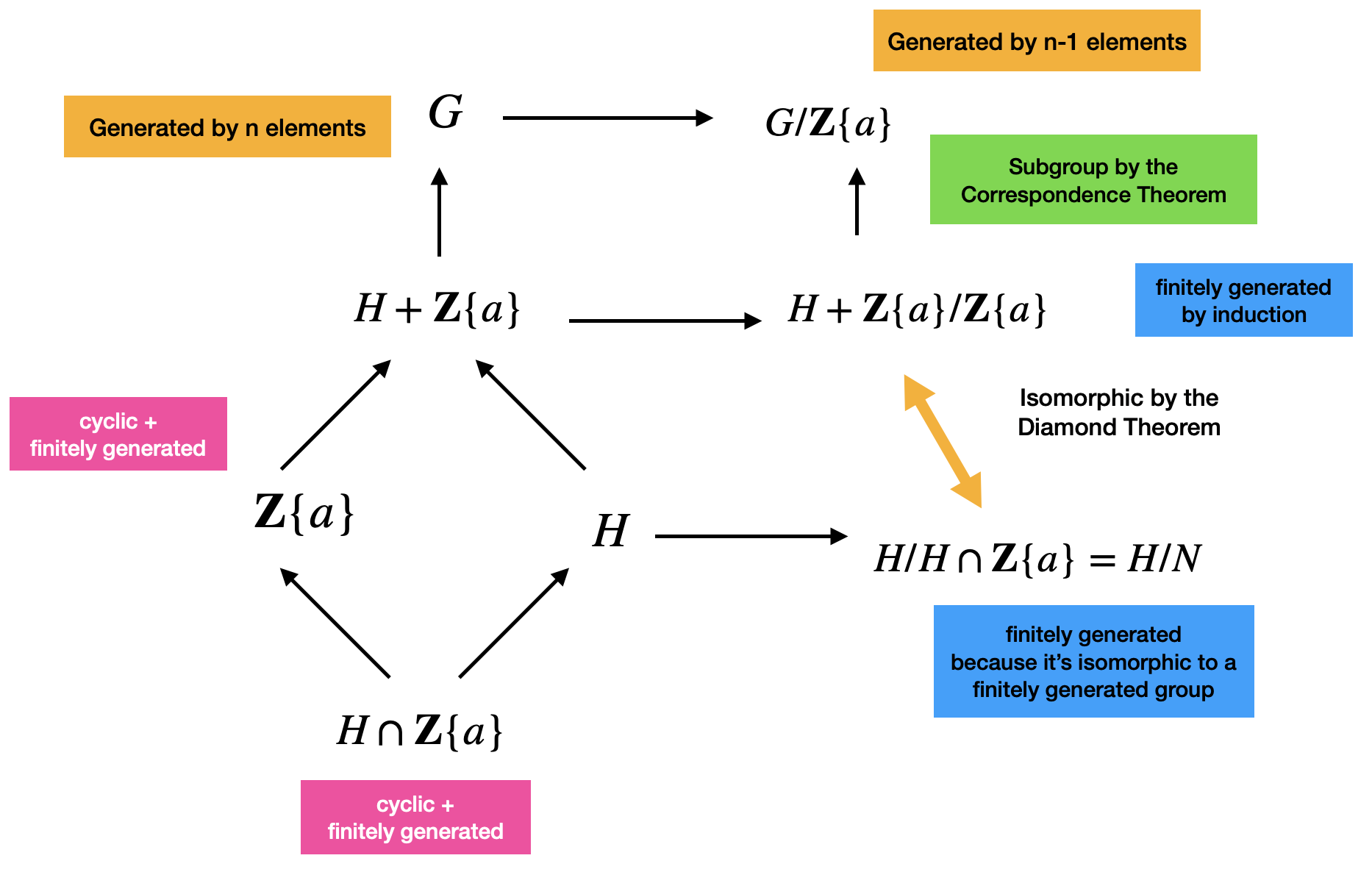
Finally, we can use the lemma to say that since \(H/N\) is finitely generated and since \(N\) is finitely generated, then \(H\) is finitely generated as we wanted to show. \(\ \blacksquare\)


Consequences

So now, recall the proposition we introduced where if \(G\) is finitely generated and abelian then there exists a surjective homomorphism \(\phi: \mathbf{Z}^n \rightarrow G\). So by the isomorphism theorem, \(G\) is isomorphic to \(\mathbf{Z}^m/N\) where \(N\) is the kernel of \(\phi\) (normal subgroup of \(\mathbf{Z}^m)\).

But we just proved above that the subgroup \(N\) must also be finitely generated since \(\mathbf{Z}^m\) is finitely generated and abelian. So there exists, some \(n \geq 0\) such that \(\bar{\alpha}: \mathbf{Z}^n \rightarrow N\) is a surjective homomorphism. (why?)

So now consider the following

$$ \begin{align*} \mathbf{Z}^n \xrightarrow{\bar{\alpha}} N \xrightarrow{i} \mathbf{Z}^m \end{align*} $$

Consider \(\alpha: i \circ \bar{\alpha}\). We know that \(\alpha(\mathbf{Z}^n) = N\). \(\alpha\) is a homomorphism since it’s the composition \(i \circ \bar{\alpha}\). Therefore, the isomorphism \(G \cong \mathbf{Z}^m/N\) can be written as \(G \cong \mathbf{Z}^m/\alpha(\mathbf{Z}^n)\).


Studying the Homomorphism from \(\mathbf{Z^n}\) to \(\mathbf{Z^m}\)

So now the goal is to show that \(\alpha: \mathbf{Z}^n \rightarrow \mathbf{Z}^m\) can be represented with a left multiplication by a matrix \(L_A\). Observe that if we take any matrix \(A \in \text{Mat}_{m \times n}(\mathbf{Z})\), we can define the following

$$ \begin{align*} L_A: \mathbf{Z}^n &\rightarrow \mathbf{Z}^m \\ L_A(c_1,...,c_n) &= (\sum_{j=1}^n a_{1j}c_j, \sum_{j=1}^n a_{2j}c_j, ..., \sum_{j=1}^n a_{mj}c_j) \\ L_A\big(\begin{pmatrix}c_1 \\ c_2 \\ \vdots \\ c_n \end{pmatrix}\big) &= A \begin{pmatrix}c_1 \\ c_2 \\ \vdots \\ c_n \end{pmatrix} \in \begin{pmatrix}d_1 \\ d_2 \\ \vdots \\ d_n \end{pmatrix} \in \mathbf{Z}^m \end{align*} $$

We claim that \(L_A\) is a homomorphism. (We won’t prove this). Basically, any homomorphism can be represented with a matrix. To find the matrix, all we need is to plug in the standard basis vectors into \(\alpha\) to get the matrix \(A\) (column vectors).

Moreover, \(\alpha: \mathbf{Z}^n \rightarrow \mathbf{Z}^m\) is equal to \(L_A\) for a unique \(A \in \text{Mat}_{m \times n}(\mathbf{Z})\). Furthermore, if \(A \in \text{Mat}_{m \times n}(\mathbf{Z})\) and \(B \in \text{Mat}_{m \times p}(\mathbf{Z})\), then \(L_{AB} = L_A \circ L_B\)


The Homomorphism \(\alpha\)

Suppose now that \(L_A: \mathbf{Z}^n \rightarrow \mathbf{Z}^m\) is an isomorphism. Then \((L_A)^{-1}\) is also an isomorphism. If we let \(L_B = (L_A)^{-1}\), then

$$ \begin{align*} L_{BA} &= L_B \circ L_A = id_{\mathbf{Z}^n} \\ L_{AB} &= L_A \circ L_B = id_{\mathbf{Z}^m} \end{align*} $$

So \(AB = I\) and \(BA = I\). So by linear algebra (over the linear algebra), \(m = n\). Therefore, we can’t really have an isomorphism unless \(m = n\).


Smith Normal Form

A matrix \(A\) is in Smith normal form if

$$ \begin{align*} A = \begin{pmatrix} d_1 & 0 & \cdots & 0 & 0 \\ 0 & d_2 & \ddots & \ddots & 0 \\ 0 & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & d_s & 0 \\ \end{pmatrix} \end{align*} $$

where \(d_i \ | \ d_{i+1}\). Then

Proposition
If \(A = diag(d_1,...,d_s \in \text{Mat}_{m \times n}(\mathbf{Z})\). Then $$ \begin{align*} \mathbf{Z}^m/L_A(\mathbf{Z}^n) \cong \mathbf{Z}/\mathbf{Z}_{d_1} \times ... \times \mathbf{Z}/\mathbf{Z}_{d_s} \times \mathbf{Z}/\mathbf{Z}^{m-s} = G \end{align*} $$


Proof
Let \(\phi\) be defined as

$$ \begin{align*} \phi: \mathbf{Z}^m &\longrightarrow G\\ (x_1,...x_s,x_{s+1},..,x_m) &= ([x_1]_{d_1}, ..., [x_s]_{d_s}, x_{s+1},...,x_m) \\ \end{align*} $$

\(\phi\) is surjective and \(\ker(\phi) = L_A(\mathbf{Z}^n)\). This is because all the entries \(x_{s+1}...x_m\) must be zero and the earlier entries must be divisible by \(d_i\).

Proposition
If \(B = PAQ\) where \(A, B \in \text{Mat}_{m \times n}(\mathbf{Z})\). Suppose that \(P,Q\) are integer invertible. Then $$ \begin{align*} \mathbf{Z}^m/L_A(\mathbf{Z}^n) \cong \mathbf{Z}^m/L_B(\mathbf{Z}^n) \end{align*} $$ We say that \(A \sim B\) are equivalent.


Proof
Let

$$ \begin{align*} \pi_A: \mathbf{Z}^m &\rightarrow \mathbf{Z}^m/L_A(\mathbf{Z}^n) \\ \pi_B: \mathbf{Z}^m &\rightarrow \mathbf{Z}^m/L_B(\mathbf{Z}^n) \end{align*} $$

Then

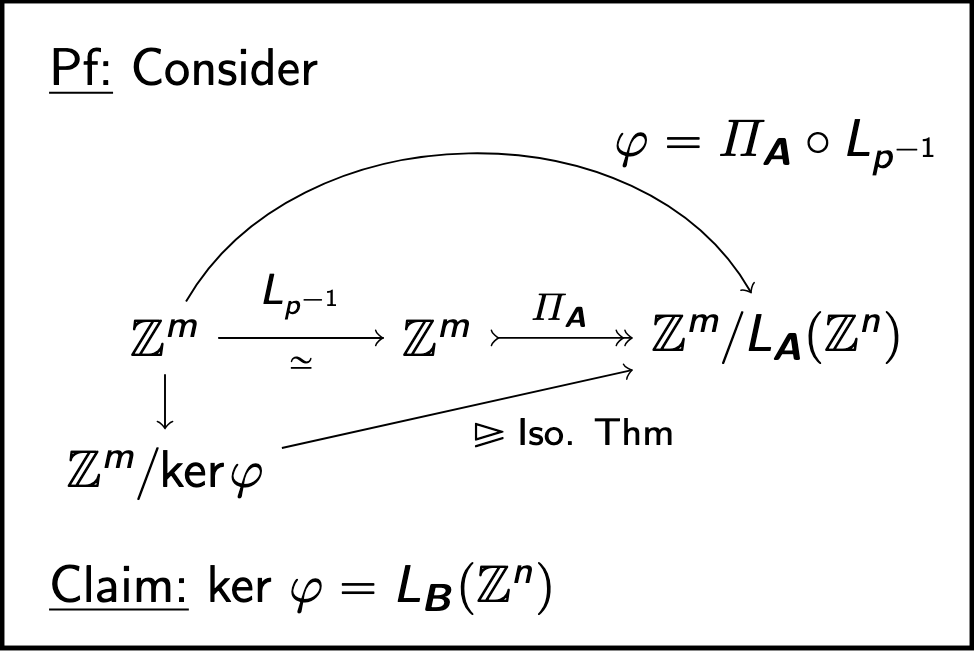
So the claim is that the kernel of this isomorphism is exactly \(L_B(\mathbf{Z}^n)\). Why?

$$ \begin{align*} z \in \ker(\phi) &\implies P_x^{-1} \in \ker(\pi_A) \\ &\implies P_x^{-1} \in Ay \text{ for some } y \in \mathbf{Z}^n \\ &\implies P_x^{-1} \in AQz \text{ for some } z \in \mathbf{Z}^n, z = Q^{-1}y \\ &\implies x \in PAQz \text{ for some } z \in \mathbf{Z}^n, z = Q^{-1}y \\ \end{align*} $$

There are 30 minutes left of this proof ….. [TODO]




References