Example 1

Let \(Q_8 = \{1, -1, i, i, j, -j, k, -k\}\) be a group. We have the identities:

$$ \begin{align*} i^2 = j^2 = k^2 = -1, \quad ij = k, \quad ji = -k, \quad ijk = -1 \end{align*} $$


\(ij = k\) is going in a clockwise direction while \(ji = -k\) is going in a counter clockwise direction. TODO: Group diagram.

There are three cyclic subgroups of order 4: \(\langle i \rangle\), \(\langle j \rangle\) and \(\langle k \rangle\). There is one cyclic group of order 2: \(\langle -1 \rangle\). Note that \(\langle i \rangle = \{1, i, -1, -i\}\).

Let’s find the cosets of \(\langle i \rangle\) in \(Q_8\).

$$ \begin{align*} j\langle i \rangle &= j\{1, i, -1, -i\} = \{j, -k, -j, k\} \\ \langle i \rangle j &= \{1, i, -1, -i\}j = \{j, k, -j, -k\} \end{align*} $$

Note that \(Q_8\) is generated by two elements \(\langle i, j \rangle\) (easy to check). Therefore, since \(j\langle i \rangle = \langle i \rangle j\) and we checked all the generators of the group, then \(\langle i \rangle\) is a normal subgroup.

Let’s study the quotient group \(Q_8 / \langle i \rangle\). We know that it must contain two elements (By Lagrange’s Theorem).

$$ \begin{align*} Q_8 / \langle i \rangle = \{\langle i \rangle, j \langle i \rangle\} \end{align*} $$



Recall, that we defined the multiplication of cosets by \((xN)(yN)=(xy)N\). Since we have two elements, observe that \(\langle i \rangle \langle i \rangle = \langle i \rangle\). Multiply \(j \langle i \rangle\) by \(\langle i \rangle\) is just \(j \langle i \rangle\). Remember that \(\langle i \rangle\) acts as the identity element/coset here. So the only interesting product is \((j\langle i \rangle) (j\langle i \rangle)\) [TODO: add a table]

$$ \begin{align*} (j\langle i \rangle) (j\langle i \rangle) &= j^2 \langle i \rangle = -\langle i \rangle = \langle i \rangle. \end{align*} $$

This multiplication table looks like the multiplication table of \(\mathbf{Z}_2\). In fact \(Q_8 / \langle i \rangle \cong \mathbf{Z}_2\).


Example 2

Taking \(Q_8\) from before, let’s look at at the cyclic group generated by \(\langle -1 \rangle\).

$$ \begin{align*} \langle -1 \rangle &= \{-1, 1\} \end{align*} $$

\(\langle -1 \rangle\) is a normal subgroup (easy check, every element in the subgroup commutes with all elements in \(Q_8\)). So we now look at the quotient structure. (the cosets of \(\langle -1 \rangle\) in \(Q_8\))

$$ \begin{align*} i \langle -1 \rangle &= \{-i, i\} \\ j \langle -1 \rangle &= \{-j, j\} \\ k \langle -1 \rangle &= \{-k, k\} \\ Q_8 / \langle -1 \rangle &= \{i \langle -1 \rangle , i \langle -1 \rangle, j \langle -1 \rangle, k \langle -1 \rangle \} \end{align*} $$

Let’s calculate the order of each element. For example, \((i \langle -1 \rangle)^2 = -1\langle -1 \rangle = \langle -1 \rangle\). So \(o(i\langle -1 \rangle) = 2\). In fact, we also have \(o(j\langle -1 \rangle) = 2\) and \(o(k\langle -1 \rangle) = 2\). This isn’t cyclic so this group must be isomorphic to the non-cyclic group of order 4. So it’s isomorphic to \(\mathbf{Z}_2 \times \mathbf{Z}_2\).


Example 3

Suppose that we are given

$$ \begin{align*} \phi: \mathbf{Z} &\rightarrow \mathbf{Z}_n \\ &\phi(m) = [m] = \{k \in \mathbf{Z} \ | \ k \equiv m (\bmod n)\} \end{align*} $$

We want to show that \(\phi(m)\) is surjective. This is because for all \(0 \leq m \leq m - 1\), \(\phi(m) = [m]\) So we are able to hit every value of \(m\). It is also a homomorphism. since

$$ \begin{align*} \phi(m_1 + m_2) = [m_1 + m_2] = [m_1] + [m_2] = \phi(m_1) + \phi(m_2) \end{align*} $$

The kernel of \(\phi\) is

$$ \begin{align*} \ker(\phi) &= \{ m \in \mathbf{Z} \ | \ [m] = [0]\} \\ &= \{0, \pm n, \pm 2n,....\} = n\mathbf{Z} \end{align*} $$

So now we have \(\ker(\phi) = n\mathbf{Z}\). We know that it is normal. We also showed that \(\phi\) is a surjective homomorphism. Therefore, by the Isomorphism Theorem, \(\mathbf{Z}/n\mathbf{Z} \cong \mathbf{Z}_n\).


Example 4

Next, let’s take

$$ \begin{align*} \phi: \mathbf{Z}_4 &\rightarrow \mathbf{Z}_2 \\ &\phi([m]_4) = [m]_2 \end{align*} $$

Here, it is not obvious this is well-defined. So let’s check that it is. Suppose that \([m_1]_4 = [m_2]_4\). We want to show that \(\phi([m_1]_4) = \phi([m_2]_4)\). Observe that

$$ \begin{align*} [m_1]_4 &= [m_2]_4 \\ [m_1]_4 - [m_2]_4 &= [0]_4 \\ [m_1 - m_2]_4 &= [0]_4 \\ m_1-m_2 &\equiv 0 \bmod 4 \end{align*} $$

This says that \(m_1 - m_2\) must be a multiple of 4 so \(m_1 - m_2 = 4k = 2(2k)\) for some \(k \in \mathbf{Z}\). So \(m_1 - m_2\) is also a multiple of 2. Therefore, \(m_1-m_2 \equiv 0 \bmod 2\) and so \([m_1]_2 = [m_2]_2\).

\(\phi\) is also a homomorphism. since

$$ \begin{align*} \phi([m_1]_4 + [m_2]_4) = \phi([m_1 + m_2]_4) = [m_1 + m_2]_2 = [m_1]_2 + [m_2]_2 = \phi(m_1) + \phi(m_2). \end{align*} $$

Next we want to show that \(\phi\) is surjective. Notice that there are two values in the target domain. \([0]_2\) and \([1]_2\). Also note that \(\phi([0]_4) = [0]_2\) and \(\phi([1]_4) = [1]_2\) so it is surjective.

The kernel of \(\phi\) is

$$ \begin{align*} \ker(\phi) &= \{ [m]_4 \in \mathbf{Z}_4 \ | \ \phi([m]_4) = [0]_2\} \\ &= \{ [m]_4 \in \mathbf{Z}_4 \ | \ [m]_2 = [0]_2\} \\ &= \{ [0]_4, [2]_4 \} = \langle [2]_4 \rangle = 2\mathbf{Z}_4 \\ \end{align*} $$

So now we have \(\ker(\phi) = \langle [2]_4 \rangle\). We know that it is normal. We also showed that \(\phi\) is a surjective homomorphism. Therefore, by the Isomorphism Theorem, \(\mathbf{Z}_4/\langle [2]_4 \rangle \cong \mathbf{Z}_2\).


Example 5

Next, let’s take

$$ \begin{align*} \phi: \mathbf{Z}_6 &\rightarrow \mathbf{Z}_{15} \end{align*} $$

We need to figure out a homomorphism. First recall that for any element, \(|\phi(x)| \ | \ |x|\). Let’s list the order of the elements in \(\mathbf{Z}_{15}\). Notice here that \(\mathbf{Z}_{15}\) is a cyclic group (with addition) so the order of any element \(g + a\) is going to be \(\frac{15}{gcd(a,15)}\)

$$ \begin{align*} &o(1): [0]_{15} \\ &o(3): [5]_{15}, [10]_{15} \\ &o(5): [3]_{15}, [6]_{15}, [9]_{15}, [12]_{15} \\ &o(15): [1]_{15}, [2]_{15}, [4]_{15}, [7]_{15}, [11]_{15}, [13]_{15}, [14]_{15} \\ \end{align*} $$

So now let’s pick \([1]_{6}\). It is a generator for \(\mathbf{Z}_{6}\). We know that \(\phi([1]_6)\) must divide the order of the element itself so \(|[1]_6| = 6\). So that tells us that \(|\phi([1]_6)|\) must be either 1,2,3 or 6. 2 and 6 are not possibilities so we don’t have any elements of that order in \(\mathbf{Z}_{15}\). So it’s either 1 or 3.

Case 1: Suppose we pick some element of order 1. That means that \(\phi([1]_6) = 1\). This implies that \(\phi([1]_6) = [0]_{15}\). Since it’s a generator, then \(\ker(\phi) = \mathbf{Z}_6\). And \(Im(\phi) = \{[0]_{15}\}\). This gives us \(\mathbf{Z}_6/\mathbf{Z}_6 = \{[0]_{15}\} \leq \mathbf{Z}_{15}\). So it’s pretty boring.

Case 2: Suppose we pick some element of order 3 so \(|\phi([1]_6)| = 3\). So let \(\phi([1]_6) = [5]_{15}\). Based on this, where will \([2]_6\) will go? Remember that we want \(\phi\) to be a homomorphism. This means that we want this to be true. That \(\phi([2]_6) = \phi([1 + 1]_6) = \phi([1]_6) + \phi([1]_6) = [5]_{15} + [5_{15} = [10]_{15}\). So we want to pick \([10]_{15}\) for \([2]_6\). Based on this, the elements will get mapped to

$$ \begin{align*} [0]_6 &\rightarrow [0]_{15} \\ [1]_6 &\rightarrow [5]_{15} \\ [2]_6 &\rightarrow [10]_{15} \\ [3]_6 &\rightarrow [0]_{15} \\ [4]_6 &\rightarrow [5]_{15} \\ [5]_6 &\rightarrow [10]_{15}. \end{align*} $$

So the image of our homomorphism is

$$ \begin{align*} Im(\phi) = \{[0]_{15}, [5]_{15}, [10]_{15}\} = \langle [5]_{15} \rangle \cong \mathbf{Z}_3 \end{align*} $$

The last statement is because all cyclic groups of order 3 are isomorphic to \(\mathbf{Z}_3\). The kernel of \(\phi\) is

$$ \begin{align*} \ker(\phi) &= \{ [m]_6 \in \mathbf{Z}_6 \ | \ \phi([m]_6) = [0]_{15}\} \\ &= \{ [0]_6, [3]_{6} \} = \langle [3]_6 \rangle \cong \mathbf{Z}_2\\ \end{align*} $$

By the Isomorphism Theorem, \(\mathbf{Z}_{6}/\langle [3]_6 \rangle \cong \langle [5]_{15} \rangle \cong \mathbf{Z}_3\).


Example 6

Next, let’s take

$$ \begin{align*} D_n = \langle r,s \ | \ r^n = s^2 = e, rs = sr^{n-1} \rangle \end{align*} $$

To define a homomorphism, we need these defining identities to hold on both sides. So let’s define

$$ \begin{align*} \phi: D_n &\rightarrow \mathbf{Z}_2 \\ r &\rightarrow 0 \quad \text{we don't to write $[0]_2$ since it's clear} \\ s &\rightarrow 1 \end{align*} $$

So now we need to verify that the three defining relations are satisfied. For example, we know that \(r^n = e\). So we want \(\phi(r^n) = \phi(e) = [0]\). But this is also

$$ \begin{align*} \phi(r^n) = \phi(rr...r) = \phi(r)+...\phi(r) = 0+...+0 = 0. \end{align*} $$

Similarly, we have \(\phi(s^2) = \phi(e) = [0]\) and at the same time

$$ \begin{align*} \phi(s^2) = \phi(ss) = \phi(s)+\phi(s) = 1 + 1 = 0 \end{align*} $$

Finally, we have \(\phi(rs) = \phi(sr^{n-1})\). We can check both sides

$$ \begin{align*} \phi(rs) &= \phi(r) + \phi(s) = 1 + 0 = 1 \\ \phi(sr^{n-1}) &= \phi(s) + \phi(r) + ... + \phi(r) = 1 + 0 + ... + 0 = 1 \end{align*} $$

Next, we need to see that it is surjective but that’s trivial since we’re sending \(r\) to \(0\) and \(s\) to \(1\) so it’s definitely surjective. The image of \(\phi\) is \(\mathbf{Z}_2\). The kernel is also easy to see

$$ \begin{align*} \ker(\phi) &= \{ l \in D_n \ | \ \phi(l) = 0\} \\ &= \langle r \rangle \\ \end{align*} $$

This is because any rotation is sent to 0 and any reflection \(\phi(r^ks) = \phi(sr^{n-k} = 1\).
By the Isomorphism Theorem, \(D_n/\langle r \rangle \cong \mathbf{Z}_2\).


Example 7

Let’s continue with the dihedral group and suppose we have

$$ \begin{align*} D_n = \langle r,s \ | \ r^n = s^2 = e, rs = sr^{n-1} \rangle \end{align*} $$

To define a homomorphism, we need these defining identities to hold on both sides. So let’s define

$$ \begin{align*} \phi: D_n &\rightarrow \mathbf{Z}_n \\ r &\rightarrow 1 \\ s &\rightarrow 0 \end{align*} $$

Is this a homomorphism? Let’s check the identity \(\phi(rs) = \phi(sr^{n-1})\). We can check both sides

$$ \begin{align*} \phi(rs) &= \phi(r) + \phi(s) = 1 + 0 = 1 \\ \phi(sr^{n-1}) &= \phi(s) + (\phi(r) + ... + \phi(r)) = 0 + n - 1 = n - 1. \end{align*} $$

Note that \(1 \not\equiv n - 1 \bmod n\) unless \(n = 2\). So it’s not a homomorphism for any \(n > 2\).


Example 8

Let’s take another dihedral group example. Define

$$ \begin{align*} D_{2n} = \langle r,s \ | \ r^{2n} = s^2 = e, rs = sr^{2n-1} \rangle \end{align*} $$

And then define

$$ \begin{align*} \phi: D_{2n} &\rightarrow \mathbf{Z}_2 \\ r &\rightarrow 1 \\ s &\rightarrow 0 \end{align*} $$

We need to verify that the three defining relations are satisfied. For example, we know that \(r^{2n} = e\). So we want \(\phi(r^{2n}) = \phi(e) = [0]\). But this is also

$$ \begin{align*} \phi(r^{2n}) = 2n\phi(r) = [2n]_2 = 0. \end{align*} $$

Similarly, we have \(\phi(s^2) = \phi(e) = [0]\) and at the same time

$$ \begin{align*} \phi(s^2) = \phi(ss) = \phi(s)+\phi(s) = 0 \end{align*} $$

Finally, we have \(\phi(rs) = \phi(sr^{n-1})\). We can check both sides

$$ \begin{align*} \phi(rs) &= \phi(r) + \phi(s) = 1 + 0 = 1 \\ \phi(sr^{2n-1}) &= 0 + 2n-1 = [2n-1]_2 = 1 \end{align*} $$

So \(\phi\) is a homomorphism. It is surjective since we hit both elements in the target. Next we’ll calculate the kernel.

$$ \begin{align*} \ker(\phi) &= \{ l \in D_n \ | \ \phi(l) = [0]_2\} \\ &= \{e, r^2, r^4 ... r^{2n-2}, s, sr^2 ... sr^{2n-2} \} \\ &= \langle s, r^2 \rangle \leq D_{2n}\\ &= \langle s, r^2 \ | \ s^2=(r^2)^{n} = e, r^2s = s(r^2)^{n-1} \rangle \cong D_n \end{align*} $$

By the Isomorphism Theorem, \(D_{2n}/D_n \cong \mathbf{Z}_2\).


Example 11

Suppose now we have the following map

$$ \begin{align*} \phi: D_{6} &\rightarrow S_6 \\ r &\rightarrow (1 \ 2 \ 3 \ 4 \ 5 \ 6) \\ s &\rightarrow (1 \ 6)(2 \ 5)(3 \ 4) \end{align*} $$

This is easy to see if we draw a hexagon and label the vertices as follows

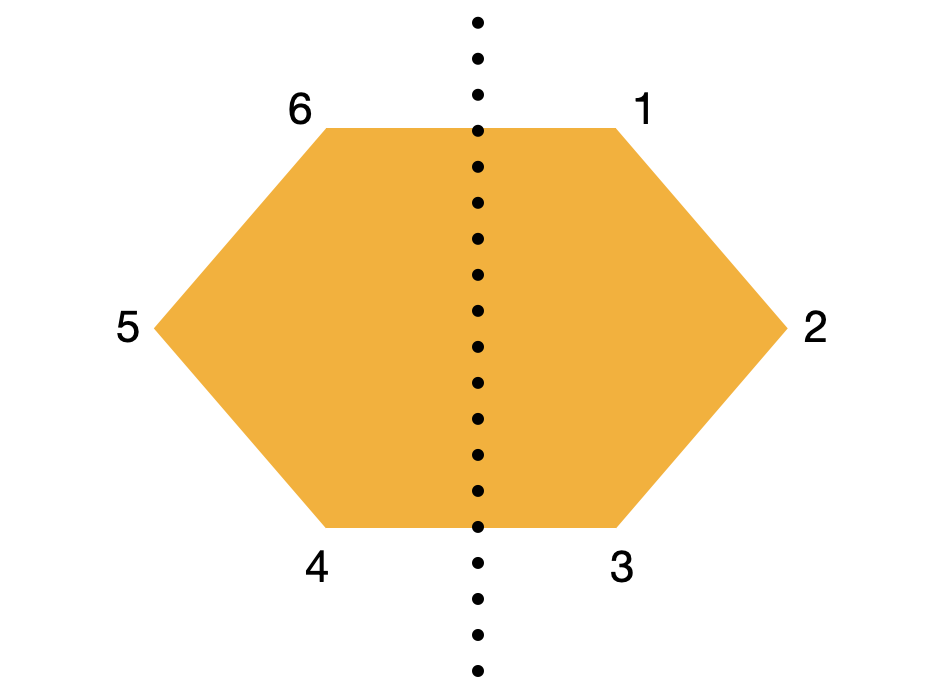
So we can see that a reflection about the \(y\) axis is represented by the above map. So now we want to check if \(\phi\) defines a homomorphism. We do this by checking the defining relations in \(D_6\) So we want \(\phi(r^6) = \phi(e) = (1) = e_{S_6}\). But this is also

$$ \begin{align*} \phi(r^6) = (1 \ 2 \ 3 \ 4 \ 5 \ 6)^6 = e \end{align*} $$

Similarly, we have \(\phi(s^2) = \phi(e) = [0]\) and it easy to check that we do get \(\phi(s^2) = e\). Finally, we have \(\phi(rs) = \phi(sr^{5})\). We can check both sides

$$ \begin{align*} \phi(rs) &= (1 \ 2 \ 3 \ 4 \ 5 \ 6) (1 \ 6)(2 \ 5)(3 \ 4) = (1)(2 \ 6)(3 \ 5)(4) = (2 \ 6)(3 \ 5) \\ \phi(sr^{n-1}) &= (1 \ 6)(2 \ 5)(3 \ 4) (1 \ 2 \ 3 \ 4 \ 5 \ 6)^5 \\ &= (1 \ 6)(2 \ 5)(3 \ 4) (1 \ 6 \ 5 \ 4 \ 3 \ 2) \quad \text{(we can count by 5)} \\ &= (1)(2 \ 6)(3 \ 5)(4) = (2 \ 6)(3 \ 5) \end{align*} $$

The image of \(\phi\) is going to be generating by \((1 \ 2 \ 3 \ 4 \ 5 \ 6)\) and \((1 \ 6)(2 \ 5)(3 \ 4)\)

$$ \begin{align*} im(\phi) &= \langle (1 \ 2 \ 3 \ 4 \ 5 \ 6), (1 \ 6)(2 \ 5)(3 \ 4) \rangle \\ \end{align*} $$

We claim that the kernel only contains the identity. Why? note that \(|r| = 6\) and the order of its image is \(|(1 \ 2 \ 3 \ 4 \ 5 \ 6)|\). This tells us

$$ \begin{align*} \ker(\phi) &= \{ l \in D_n \ | \ \phi(l) = 0\} \\ &= \langle r \rangle \\ \end{align*} $$




References