Last time we introduced both the Homomorphism Theorem. Recall that if $G$ is a group and $N$ was a normal subgroup of $G$. And then we had a homomorphism $\varphi: G \rightarrow H$ such that the kernel of $\phi$ is contained in $N$ (or easier to remember, $\phi(N) = \{e\}$). Then we get

$$ \begin{align*} \varphi':G/N &\rightarrow H \\ \phi'(xn) &= \phi(x) \end{align*} $$

Then we studied the Isomorphism Theorem which requires additionally that the homomorphism $\varphi:G \rightarrow H$ to be surjective as well as $N = \ker(\varphi)$. Then, this will then get us an isomorphism $\varphi': G/N \rightarrow H$.

The Correspondence Theorem relates the subgroups of the quotient group $G/N$ to the subgroups of $G$ that contain $N$.

The theorem claims that there is a bijection or a bijective correspondance between the two groups.

Correspondence Theorem

Let $G$ be a group and let $N$ be a normal subgroup of $G$. There is a bijection between $B \leq G/N$ and the subgroup $\pi^{-1}B$ (pre-image of $B$ which is a subgroup of $G$). $$ \begin{align*} B \leq G/N \longrightarrow \pi^{-1}B \end{align*} $$

Recall that we defined the quotient homomorphism to be

$$ \begin{align*} \pi \ : \ G &\rightarrow G/N \\ \pi(x) &= xN. \end{align*} $$

Also Recall the the pre-image of $B$ is $\pi^{-1}(B) = \{g \in G \ | \ \pi(g) \in B\}$ which we showed previously to be a subgroup of $G$.

Additionally, the theorem also claims that the normal subgroups of $G/N$ correspond to the normal subgroups in $G$ containing $N$.

Example

Let $G = \mathbf{Z}$ and $N = \mathbf{Z}6$ (multiples of 6). Therefore $G/N = \mathbf{Z}/\mathbf{Z}6 = \mathbf{Z}_6$. Here is a breakdown of the subgroups of $\mathbf{Z}$. Within all of these subgroups you’ll see the $\mathbf{Z}6$. The subgroups in the red outline will correspond to the subgroups of $\mathbf{Z}/\mathbf{Z}6 = \mathbf{Z}_6$ on the left side.

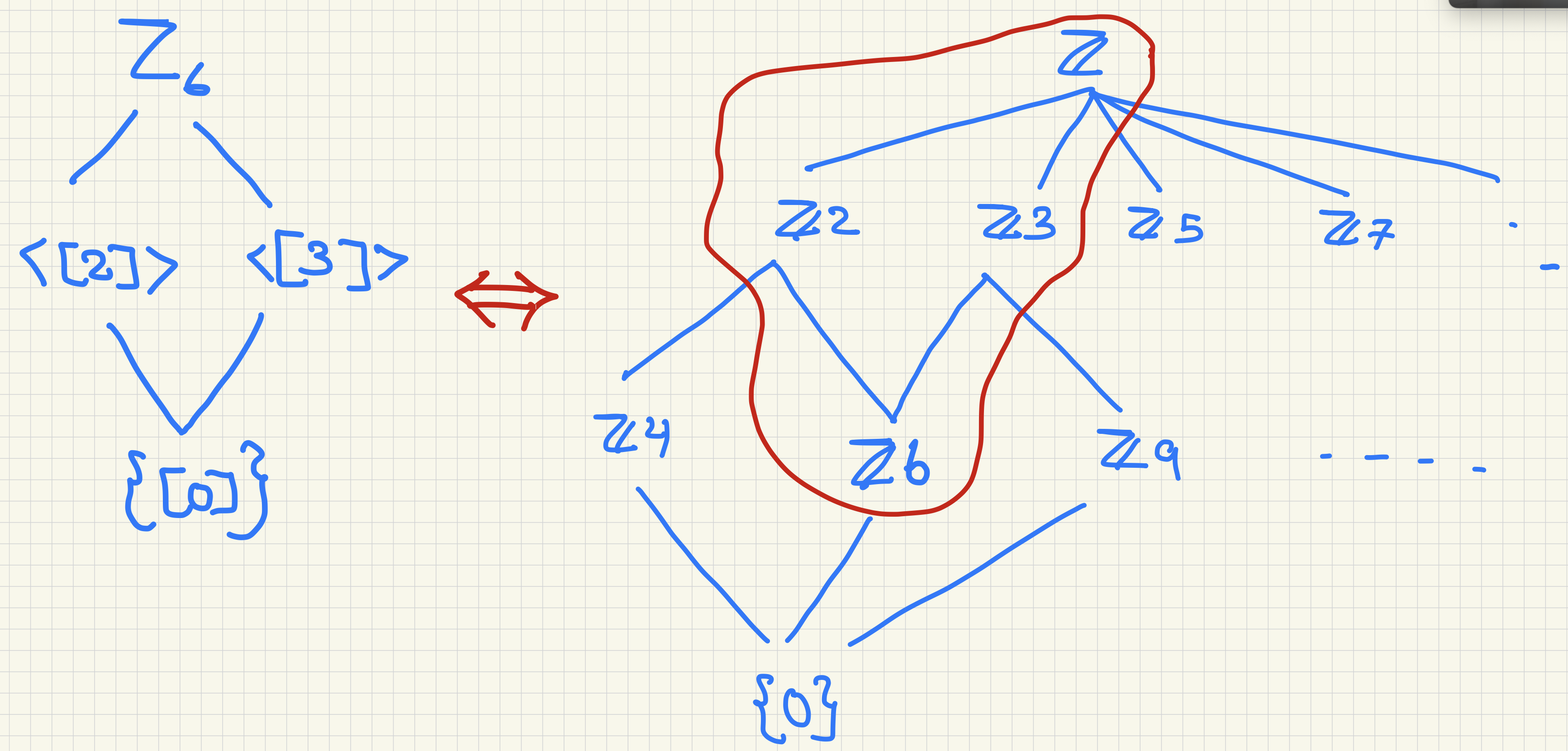
Take another example. Suppose that $N = \mathbf{Z}2$. Recall the definition of $\pi$:

$$ \begin{align*} \pi \ : \ \mathbf{Z} &\rightarrow (\mathbf{Z}/\mathbf{Z}2 = \mathbf{Z}_2) \\ \pi(x) &= x + \mathbf{Z}2. \end{align*} $$

For example $x = 3$ and $x = 6$. Then

$$ \begin{align*} \pi(3) = 3 + \mathbf{Z}2 &= \{...,3 + -4, 3 + -2, 3 + 0, 3 + 2, 3 + 4,...\} \\ &= \{..., -1, 1, 3, 5, 7...\} = [1]_2 \\ \pi(6) = 6 + \mathbf{Z}2 &= \{...,6 + -4, 6 + -2, 6 + 0, 6 + 2, 6 + 4,...\} \\ &= \{...,2, 4, 6, 8, 10...\} = [0]_2 \end{align*} $$

In general, we will have exactly two cosets. Again $\mathbf{Z}/\mathbf{Z}2$ partitions $\mathbf{Z}$ into two cosets. The coset of the even numbers and the coset of the odd numbers.

Now, we want to take their pre-image. Here the possible subsets in $\mathbf{Z}_2$ are $[0]_2$ and $[1]_2$. BUT, the subgroups of $\mathbf{Z}_2$ are only $\{[0]\}$ and $\mathbf{Z}_2$. $[1]$ is NOT a subgroup. So $B = \{\{[0]\}, \mathbf{Z}_2\}$ in

$$ \begin{align*} \pi^{-1}(B) = \{g \in \mathbf{Z} \ | \ \pi(g) \in B\} \end{align*} $$

Applying it on each subgroup, we see that

$$ \begin{align*} \pi^{-1}(\{[0]\}) &= \{g \in \mathbf{Z} \ | \ \pi(g) \in \{[0]\}\} \\ &= \{-4, -2, 0, 2, 4,.... \} \\ &= \mathbf{Z}2 \\ \pi^{-1}(\mathbf{Z}_2) &= \{g \in \mathbf{Z} \ | \ \pi(g) \in \mathbf{Z}_2\} \\ &= \mathbf{Z} \end{align*} $$

So we see here that there is a bijective correspondance between $\{[0]\}$ which is a subgroup of $\mathbf{Z}/\mathbf{Z}2 = \mathbf{Z}_2$ and $\mathbf{Z}2$ which is a subgroup of $\mathbf{Z}$.

Proof of the Correspondence Theorem

So again, we want to show that there is a bijection between the subgroup $d$ of the quotient group $G/N$ and the subgroup of $G$ which contain $N$

One way to show that there is a bijection is to show that we have an inverse function.

We can send a subgroup of the quotient group $B \leq G/N$ its pre-image $\pi^{-1}(B)$. We can easily show that $\pi^{-1}(B)$ is a subgroup of $G$. Recall that $B$ is a collection of cosets $B = \{gN \ | gN \leq G/N\}$ because it's a subgroup of the quotient group. The pre-image of $B$ are elements of $G$ such that they're the elements that make up the cosets. So if $B =\{eN, aN, bN\}$, then its pre-image is $\{e, a,b\}$ which is a subgroup of $G$. Note here that we must have the identity element $eN \in B$ since it's a subgroup. So we can see here that $N$ is definitely contained in $G$.
To go the other way. Suppose we have a subgroup of $A \leq G$ containing $N$. Now, to relate it to a subgroup inside $G/N$, take its image under $\pi$. We know $\pi(A)$ by definition are the cosets $\{\pi(a)=aN \ | \ a \in A\}$. $\pi(A)$ is a subgroup of $G/N$.

So now we need to check two things:

If $B \leq G/N$, then $\pi(\pi^{-1}(B)) = B$.
If $A \leq G$, then $\pi^{-1}(\pi(A)) = A$.

Remark: If we don’t know that $A$ contains $N$, then if $A \leq G$, we can show that $\pi(\pi(A)) = AN = \{an \ | \ a, n \in N\}$

General Correspondance Theorem

There is a more general correspondance theorem (the way it is listed in the book) which says

Correspondence Theorem

Let $\varphi: G \rightarrow H$ is a surjective homomorphism and $N = \ker(\phi)$. Then, there is a bijection correspondance between the subgroups of $H$ and the subgroups of $G$ which contain $N$.

Recall that by the Isomorphism Theorem, that $H \approx G/N$. By the previous Correspondance Theorem, we showed that subgroups of $G/N$ correspond to subgroups of $G$ containing $N$. So we’ll have this picture

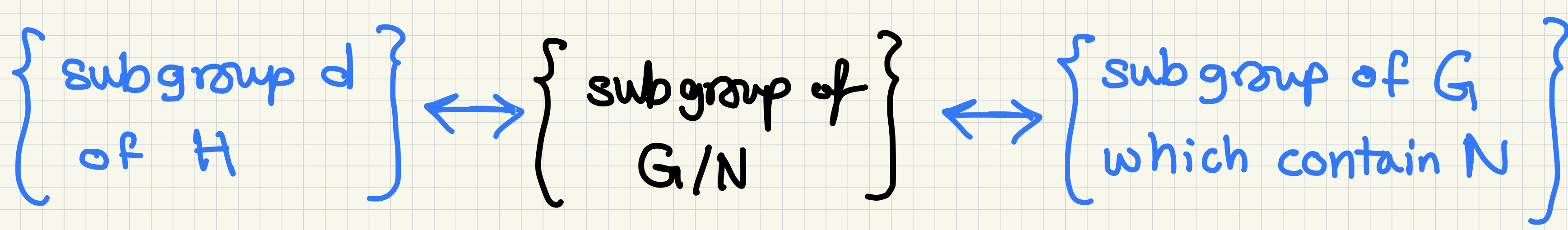
So we have $H \approx G/N$ by the Isomorphism Theorem and then we have the second part of the picture by the Correspondance Theorem.

Factorization Theorem

Let $N \leq K \leq G$ where $N$ and $K$ are normal subgroups in $G$. Define the surjective homomorphism $$ \begin{align*} \varphi \ : \ G/N &\rightarrow G/K \\ xN &\rightarrow xK \end{align*} $$ So this homomorphism takes the $N$ coset of $x$ to the $K$ coset of $x$. From this, we get an isomorphism between $(G/N) / (K/N)$ and $G/K$ so $(G/N) / (K/N) \approx G/K$ where $\ker(\varphi) = K/N$.

Note here that the kernel $K/N$ is a subgroup of $G/N$. The kernel consists of all the cosets in $G/N$ such that if we apply the homomorphism, we get the identity coset in $G/K$. In fact (show this (Exercise))

$$ \begin{align*} K/N = \{xN \ | \ \varphi(xN) = ek\} = \{xN \ | \ xN \leq K\} \end{align*} $$

Product Subsets

Definition (Product Subsets)

Let $G$ be a group with subsets $A, B \subseteq G$. Then $$ \begin{align*} AB &= \{ab \ | \ a \in A, b \in B\} \subseteq G \\ BA &= \{ba \ | \ b \in B, a \in A \} \subseteq G. \end{align*} $$

If $A$ and $B$ are subgroups of $G$, then we can have $AB \neq BA$. We can also have $AB$ and $BA$ not be subgroups themselves.

Example

Suppose $G = S_3$. Then

$$ \begin{align*} A &= \langle (1 \ 2) \rangle = \{e, (1 \ 2)\} \\ B &= \langle (1 \ 3) \rangle = \{e, (1 \ 3)\}. \end{align*} $$

Then

$$ \begin{align*} AB &= \{e, (1 \ 2), (1 \ 3), (1 \ 3 \ 2)\} \\ BA &= \{e, (1 \ 3), (1 \ 2), (1 \ 2 \ 3)\}. \end{align*} $$

We can observe that $AB$ is not a subgroup of $G$ because it is not closed. Another reason is that the order of $AB$ is 4 while the group size $|S_3| = 6$ and 4 doesn’t divide 6. $BA$ is also not a subgroup since it has 4 elements. This leads to the next proposition.

Proposition

If $A, B \leq G$, then $AB$ is a subgroup if and only if $AB = BA$.

Proof
$\Rightarrow:$ Suppose that $AB$ is a subgroup of $G$. We want to show that $AB = BA$. Let $a \in A$ and $b \in B$. So $x = ab \in AB$. But $AB$ is a subgroup, so $x^{-1} \in AB$. We can write $x^{-1} = a'b'$ where $a' \in A$ and $b' \in B$. Take the inverse of $x^{-1}$ to see that

$$ \begin{align*} (x^{-1})^{-1} &= (a'b')^{-1} \\ x &= (b')^{-1}(a')^{-1} \\ \end{align*} $$

But this shows that $(b')^{-1}(a')^{-1} \in BA$. This implies that $AB \subseteq BA$. Now, suppose that $x \in BA$. So $x = ba$ where $b \in B$ and $a \in A$. Write $ba = (eb)(ae)$. We know that $eb \in AB$ and $ea \in AB$, so $(eb)(ae)$ must be in $AB$ since $AB$ is a subgroup. So $BA \subseteq AB$. This proves that $AB = BA$ as we wanted to show.

$\Leftarrow:$ Now suppose that $AB = BA$. We want to show that $AB$ is a subgroup of $G$.

$e \in AB$. This is because $e \in A$ and $e \in B$ so $ee = e \in AB$.
$x, y \in AB$ implies that $xy \in AB$. Suppose that $a,a' \in A$ and $b,b' \in B$. Then $aba'b' = a(ba')b'$. $ba' \in AB = BA$ by the hypothesis. So we can re-write $ba'$ as $a''b''$ for some $a'' \in A$ and $b'' \in B$. So now $a(ba')b' = aa''b''b \in AB$
For Any $x \in AB$, $x^{-1} \in AB$. If $x \in AB$, then $x \in BA$ by the hypothesis. So write $x = ba$ so $x^{-1} = a^{-1}b^{-1}$. This means that $x^{-1} \in AB$.

Diamond Isomorphism Theorem

If $A, N \leq G$ where $N$ is normal, then

$AN = NA$.
$AN \leq G$. $N$ is normal in $AN$.
$A \cap N \leq A$, $A \cap N$ is normal in $A$.
$A/N \approx A/A \cap N$.

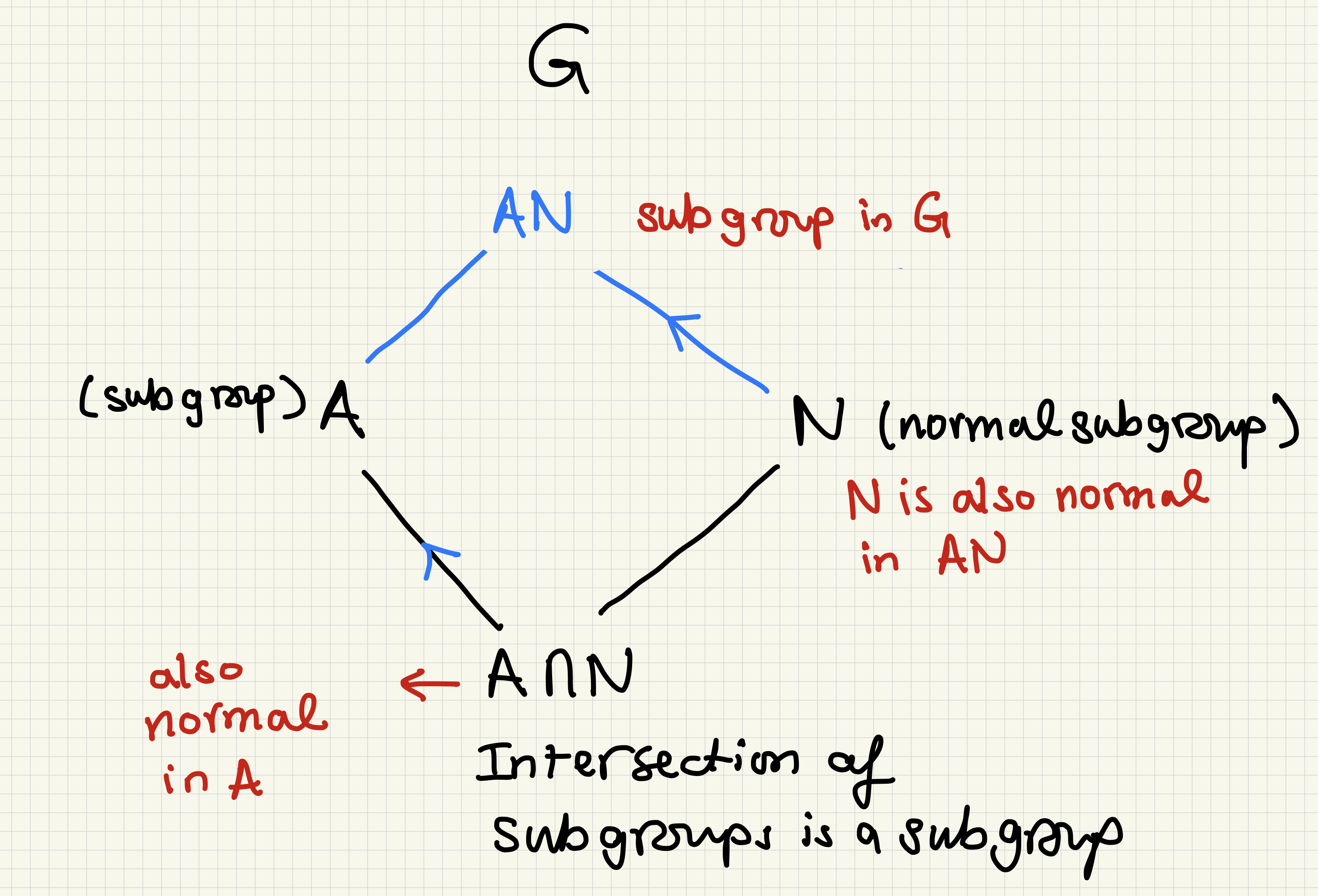
Proof in lecture notes along with an example that we will need for the next homework.

References

MATH417 by Charles Rezk
Algebra: Abstract and Concrete by Frederick M. Goodman