Definition 1.6.8
A natural number \(d\) is the greatest common divisor of integers \(a\) and \(b\) if
  1. \(d\) is a common divisor. So \(d\) divides \(a\) and \(b\)
  2. Every common divisor \(e\) also divides \(d\). In other words, if \(e \ | \ a\) and \(e \ | \ b\), then \(e \ | \ d\)


If the greatest common exists, then it is unique. Why? suppose \(d\) and \(d'\) are both greatest common divisors. Then by definition, \(d \ | \ d'\) and \(d' \ | \ d\) because every common divisor divides the gcd and they each must divide each other. But this means that \(d = \pm 'd\) by the divisibility properties from last lecture. But also by definition, \(d\) is non-negative and so \(d = 'd\). \(\ \blacksquare\)

Note that in the book \(a\) and \(b\) are nonzero in the definition. With this definition, the set of divisors of \(0\) is \(\mathbf{Z}\). If \(a = 0\) and \(b \neq 0\), then \(|a|\) is the gcd of \(a\) and \(0\). If both \(a\) and \(b\) are zero, then \(0\) is the gcd of \(0\) and \(0\).

Before addressing the question of whether the greatest common divisor exists, we’ll to define one more thing

Definition
Let \(a, b \in \mathbf{Z}\). An integer combination of \(a\) and \(b\) is any integer of the form $$ \begin{align*} I(a,b) = \{ra + sb \ | \ r, s \in \mathbf{Z}\}. \end{align*} $$


For example \(I(4,6) = \{4s + 6t \ | \ s, t \in \mathbf{Z}\}\). If we let \(s = -1\) and \(t = 1\), then \(2 \in I(4,6)\). In fact, this set produces all of the even integers. It includes all multiples of 2. In other words, we can also write that \(I(4,6) = \mathbf{Z}2\). In fact, this turns out to always be true, the set of integer combinations of two integers is also the set of multiples of a number and that number is the greatest common divisor! even when one of the integers is \(0\). So yes the GCD exists and can even be computed. Before formally proving its existence, we’ll present the way it can be computed next.


The Euclidean Algorithm

Let \(\mathbf{Z}^2 = \{(a,b), a,b \in \mathbf{Z}\}\).
Define \(F: \mathbf{Z}^2 \rightarrow \mathbf{Z}^2\) by

$$ \begin{equation*} F(m,n) = \begin{cases} (n,r), r = rem_n(m) \quad &\text{if } n \neq 0 \\ (|m|,0) \quad \quad &\text{if } n = 0\end{cases} \end{equation*} $$


\(rem_n(m)\) is the remainder of \(m \div n\) (recall that we can write \(m = qn + r\) where \(0 \leq r < |n|)\)).

Euclidean Algorithm: Iterate \(F\) until stable.

Example:

$$ \begin{align*} (42, -24) \xrightarrow{F} (-24, 18) \xrightarrow{F} (18, 12) \xrightarrow{F} (12, 6) \xrightarrow{F} (6, 0) \xrightarrow{F} (6, 0) \end{align*} $$




The GCD Theorem

So now we have an algorithm to compute the GCD algorithm. Next, we will prove that it does compute the GCD and so the GCD does exist.

Theorem
Let \(a, b \in \mathbf{Z}\). Then
  1. For \(a, b\) have a GCD \(d \geq 0\).
  2. \(I(a,b) = \mathbf{Z}d\).
  3. \(d\) is computed by the Euclidean algorithm.


We’ll start from (3) and then prove that the answer produced by the algorithm is in fact an integer combination of the original input (statement 2). Finally, we’ll show that this just means that we have computed the GCD (statement). To do all of this we will also need the following lemmas

Lemma
If \(a, b \in I(c,d)\), then \(I(a,b) \subseteq I(c,d)\)


Proof: Homework Problem

Lemma
If \(F(m,n) = (a,b)\), then \(I(m,n) = I(a,b)\)


Proof:
We have two cases:

Case 1: \(n \neq 0\). In this case, \(F(m,n) = (n, r)\) where \(r\) is the remainder after dividing \(m\) by \(n\). So \(m = qn + r\) where \(0 \leq r < |n|\). We want to show that the integer combinations of \(m\) and \(n\) is the same as the integer combinations of \(n\) and \(r\), that is, \(I(m,n) = I(n,r)\). To do this, we will show that \(I(m,n) \subseteq I(n,r)\) and \(I(n,r) \subseteq I(m,n)\). To show that \(I(m,n) \subseteq I(n,r)\), observe that \(m\) is an integer combination of \(n\) and \(r\) because we can write \(m\) as

$$ \begin{align*} m &= qn + 1r. \end{align*} $$

Similarly, \(n\) is also an integer combination of \(n\) and \(r\) because we can write \(n\) as

$$ \begin{align*} n &= 1n + 0r. \end{align*} $$

Since \(m\) and \(n\) can both be written as integer combinations of \(n\) and \(r\), that is \(m \in I(n,r)\) and \(n \in I(n,r)\), then by the previous lemma, \(I(m,n) \subseteq I(n,r)\). To see that \(I(m,n) \subseteq I(n,r)\), observe that we can write \(n\) as \(n = 0m + 1n\) so \(n \in I(m,n)\). Similarly, \(r = 1m + (-q)m\) so \(r \in I(m,n)\). Then, by the previous lemma, \(I(m,n) \subseteq I(n,r)\). Therefore, \(I(m,n) = I(n,r)\).

Case 2: \(n = 0\). In this case, \(F(m,n) = F(m,0) = (|m|,0)\). In this case the integer combinations of \(0\) and \(m\) are just multiples of \(m\) so \(I(m,0) = \mathbf{Z}m\). But this is the same as the integer combinations of \(|m|\) and \(0\) so \(\mathbf{Z}m = I(|m|,0) = I(m,0)\) which is what we wanted to show. \(\blacksquare\)


Proof of the GCD Theorem

We iterate the algorithm until \(n = 0\) and \(F(m,n) = (|m|,0)\). By the previous lemma we saw that \(I(m,n) = \mathbf{Z}d\) for some \(d \geq 0\).

Claim: \(d\) is a GCD.

  1. \(m,n \in I(m,n) = \mathbf{Z}d\). So \(m\) and \(n\) are both multiples of \(d\) and d divides both of them. \(d \ | \ m\) and \(d \ | \ n\).
  2. So now for condition 2, suppose \(e\) is a common divisor of \(m\) and \(n\). We want to show that \(e\) divides \(d\). Since \(e \ | \ m\) and \(e \ | \ n\), then \(m\) and \(n\) are both multiples of \(e\). So we can write \(m = eu\) and \(n = ev\) for some \(u,v \in \mathbf{Z}\).

    But we know that any integer combination of \(m\) and \(n\) is a multiple of \(d\). So we can write for some \(r, s \in \mathbf{Z}\)
    $$ \begin{align*} d &= rm + sn \\ &= reu + sev \\ &= e(ru + sv). \end{align*} $$
    So \(e\) must divide \(d\).

Therefore, \(d = gcd(m,n)\) as desired. \(\ \blacksquare\)
Note that the Euclidean Algorithm gives a method for computing \(r, s \in \mathbf{Z}\), so \(d = rm + sn\).


GCD Example

TODO … all I have now is this




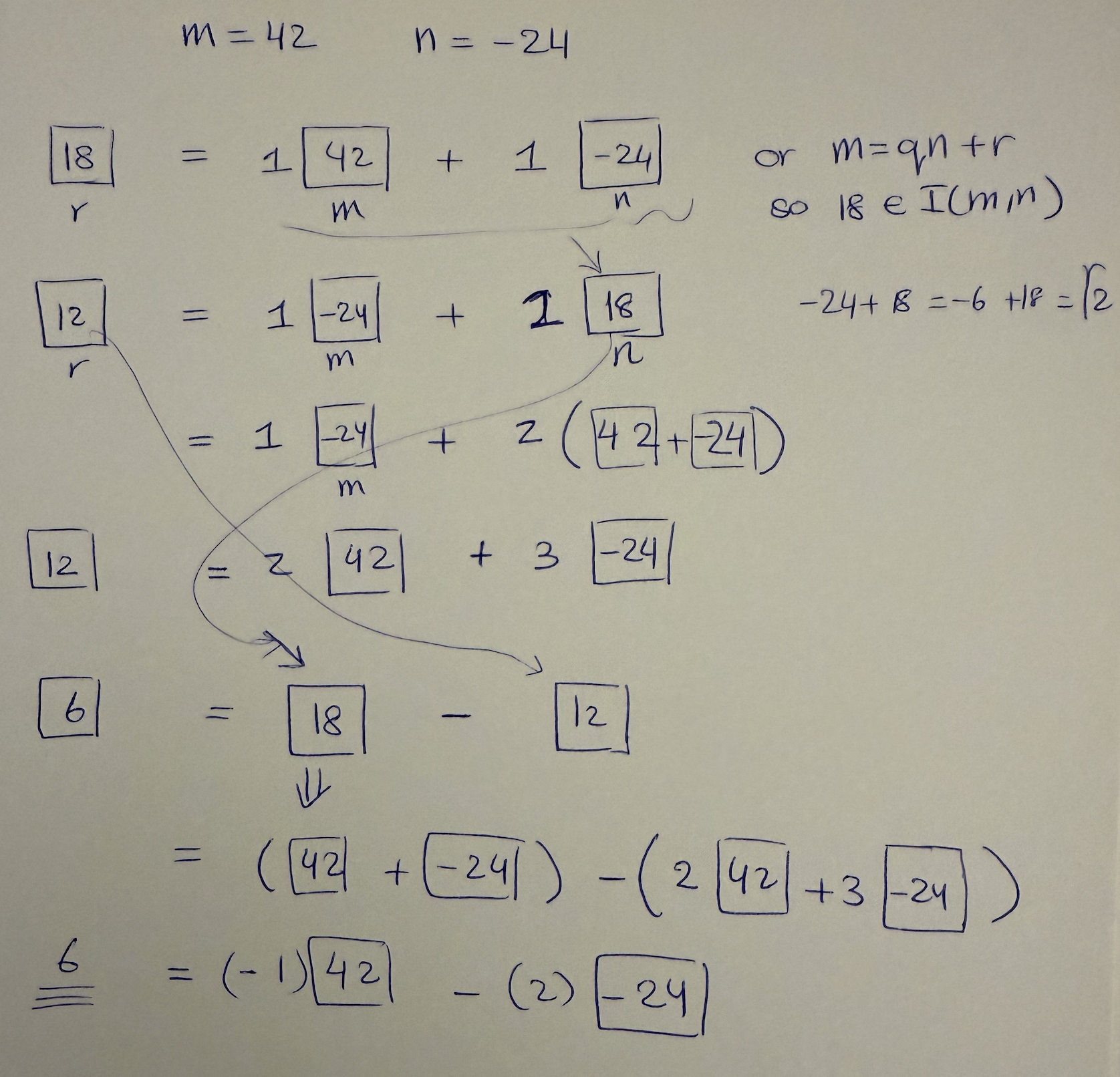
Relatively Prime Integers

Next, we’ll see how the GCD is used in the definition of relatively prime numbers.

Definition (Book Definition 1.6.14)
\(a, b \in \mathbf{Z}\) are relatively prime if gcd\((a,b) = 1\).



For example \(4\) and \(9\) are relatively prime. gcd\((4,9)=1\).

Proposition (Book Proposition 1.6.15)
\(a, b\) are relatively prime if and only if $$ \begin{align*} 1 = ra + sb \end{align*} $$ for some \(r,s \in \mathbf{Z}\)


Proof
\(\Rightarrow:\) If \(a\) and \(b\) are relatively prime, then by definition gcd\((a,b)=1\). By the GCD Theorem, this means that \(I(a,b) = 1\) and so we’re done.
\(\Leftarrow:\) If \(1 = ra + sb\) for some \(r,s \in \mathbf{Z}\), then this means that \(1 \in I(a,b)\). But \(I(a,b)\) is also the set of multiples of some integer \(m\). But since \(1\) is in the set, then it must contains all multiples of \(1\). Therefore, we must have \(1 = I(a,b)\). By the GCD Theorem, \(1\) is therefore the gcd of \(a\) and \(b\) and so \(a\) and \(b\) are relatively prime. \(\ \blacksquare\)

Proposition (Book Corollary 1.6.17)
If \(a, b\) are relatively prime and if \(a \ | \ n\) and \(b \ | \ n\), then \(ab \ | n\).


Proof
Suppose \(a\) and \(b\) are relatively prime. We are given that \(a \ | \ n\) so \(n = au\) for some \(u \in \mathbf{Z}\). Similarly, \(b \ | \ n\) and so \(n = bv\) for some \(v \in \mathbf{Z}\). Since \(a\) and \(b\) are relatively prime, then by definition gcd\((a,b)=1\). This means that \(I(a,b) = 1\) and we can write \(1 = ra + sb\) for some integers \(s, r \in \mathbf{Z}\). Multiply this equation by \(b\) as follows

$$ \begin{align*} 1 &= ra + sb \\ n &= n(ra + sb) \\ &= nra + nsb \\ &= (bv)ra + (au)sb \\ &= (ab)vr + (ab)us \\ &= (ab)(vr + us). \\ \end{align*} $$

From this we see that \(ab \ | \ n\) as desired. \(\ \blacksquare\)

Proposition
If \(p\) is prime and \(p \ | \ ab\), then either \(p \ | \ a\) or \(p \ | \ b\)


Proof
Suppose that \(p \ | \ ab\). We’ll show that if \(p \nmid a\), then \(p \ | \ b\). Since \(p\) is prime and \(p \nmid a\), then gcd\((p,a)=1\). By Proposition (1.6.15), this implies that \(1 = pr + as\) for some \(r, s \in \mathbf{Z}\). Multiply this equation by \(b\) to see that

$$ \begin{align*} 1 &= pr + as \\ b &= b(pr + as) \\ b &= p(br) + (ab)s \\ \end{align*} $$

Clearly \(p\) divides the first term. \(p\) also divides the second term by the assumption we’re given. Therefore, \(p\) must divide \(b\) as we wanted to show. \(\ \blacksquare\)

Fact: If \(p \ | \ a_1a_2...a_k\), then \(p\) divides at least one of the factors. So \(p \ | \ a_i\) for some \(i \in \{1,...,k\}\)


References