Definition
Let \(X\) be a set. Define the permutation of \(X\) as a bijection from the set to itself (\(f: X \rightarrow X\)). Let \(Sym(X)\) be the set of all bijections from \(X\) to itself (\(X \rightarrow X\)).


\(Sym(X)\) equipped with the composition of functions operation is a group. To see this observe that

  • \(id: X \rightarrow X, id(x) = x\) is the identity element.
  • Composition of functions is associative.
  • The composition of two permutations is another permutation.
  • Bijections have inverses and the inverse of a bijection is another bijection.

This group is often denoted by the Permutation Group or more often the Symmetric Group.

The standard example for the case of finite sets is the standard set \(X = \{1,2,...,n\}\). The symmetric group has a special name called \(S_n\),

$$ \begin{align*} S_n = Sym(\{1,2,...,n\}) \end{align*} $$

The size of \(S_n\) is \(|S_n| = n!\).


Two Line Notation

Let \(\rho, \psi \in S_4\), then we’ll write

$$ \begin{align*} \rho = \begin{pmatrix}1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2\end{pmatrix} \end{align*} $$

shows that \(\rho(1) = 1\), \(\rho(2) = 4\), \(\rho(3) = 3\) and \(\rho(4) = 2\). Similarly,

$$ \begin{align*} \psi = \begin{pmatrix}1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3\end{pmatrix} \end{align*} $$

shows that \(\psi(1) = 4\), \(\psi(2) = 2\), \(\psi(3) = 1\) and \(\psi(4) = 3\). Finally,

$$ \begin{align*} \rho\psi = \begin{pmatrix}1 & 2 & 3 & 4 \\ 2 & 4 & 1 & 3\end{pmatrix} \in S_4 \end{align*} $$

so \(\rho\psi(1) = 2\), \(\rho\psi(2) = 4\), \(\rho\psi(3) = 1\) and \(\rho\psi(4) = 3\).


Cycle Notation

We can decompose the cycles in each permutation above. For example for the first permutation

$$ \begin{align*} \rho = \begin{pmatrix}1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2\end{pmatrix} \end{align*} $$

We can decompose this permutation into the following

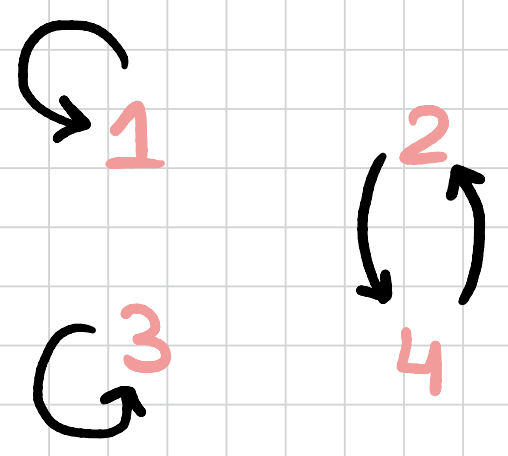
In this permutation, we have a cycle of length \(2\) For the second permutation

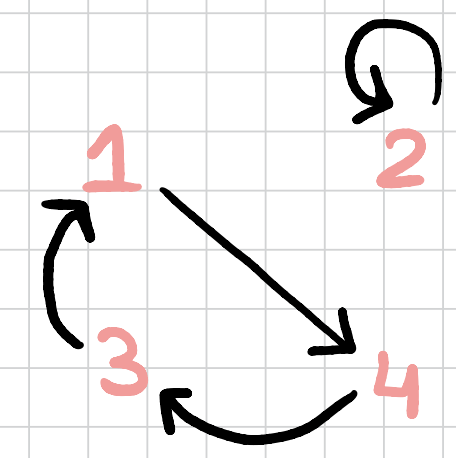
$$ \begin{align*} \psi = \begin{pmatrix}1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3\end{pmatrix} \end{align*} $$

we have a cycle of length \(3\).

To describe a cycle, we can use cycle notation which is defined as follows

Definition
Let \(\sigma = (a_1 \quad a_2 \quad ... \quad a_k)\) where \(a_1,...,a_k \in X\) are distinct. \(\sigma\) is defined by $$ \begin{align*} \sigma(a_i) &= a_{i+1}, \quad i = 1,...,k-1 \\ \sigma(a_k) &= a_1 \\ \sigma(x) &= x, \quad \text{if} x \notin \{a_1,...,a_k\} \\ \end{align*} $$


So we can write the first permutation with cycle notation as \((2,4)\) only since by definition for the other elements \(\sigma(x)=x\), while the second permutation can be written as \((1,4,3)\).

What about the following example?

$$ \begin{align*} \begin{pmatrix}1 & 2 & 3 & 4 & 5\\ 3 & 5 & 4 & 1 & 2\end{pmatrix} \end{align*} $$

Note here that we have two disjoint cycles. \((1 \quad 4 \quad 3)\) where \(1\) goes to \(3\) and \(3\) goes to \(4\) and \(4\) goes back to \(1\) and \((2 \quad 5)\) where \(2\) goes to \(5\) and \(5\) goes back to \(2\). This permutation can be written as

$$ \begin{align*} (1 \quad 3 \quad 4)(2 \quad 5) \end{align*} $$

Facts

Some facts about the cycle notation

  • \((1) = (2) = ... (n) = id\). All of these represent the identity permutations.
  • The order of the elements in a cycle matters up to "cyclic permutation". \((1 \quad 2 \quad 3 \quad 4) = (2 \quad 3 \quad 4 \quad 1) \neq (1 \quad 3 \quad 4 \quad 2)\)
  • For the inverse of a permutation, we just reverse the order of elements so \((a_1 \quad a_2 \quad ... \quad a_k)^{-1} = (a_k \quad a_{k-1} \quad ... \quad a_1)\)
  • Two cycles \(\sigma = (a_1 \quad a_2 \quad ... \quad a_k)\) and \(\tau = (b_1 \quad b_{2} \quad ... \quad b_l) \in Sym(X)\) are disjoint if \(\{a_1,a_2,...,a_k\} \cap \{b_1,b_2,...,b_l\} = \emptyset\). Moreover, if the two sets are disjoint, then \(\sigma \circ \tau = \tau \circ \sigma\). This means that the permutation above that we described with \((1 \quad 3 \quad 4)(2 \quad 5)\) can also be written as \((2 \quad 5)(1 \quad 3 \quad 4)\)


Theorem
Every non-id element in \(Sym(X)\) where \(X\) is finite can be written as a product of pairwise disjoint cycles (of length \(\geq 2\) uniquely up to re-ordering.


Suppose we have \(\sigma = (1 \quad 3)(2 \quad 7 \quad 8)(4 \quad 5 \quad 6)(9) \in S_9\). Any of the cycles in this notation are pairwise disjoint. We have 3 disjoint cycles where \(9\) is fixed.

The proof for this theorem is in the class notes.


Cycle Type

We can classify permutations of a finite set into groups corresponding to the number of cycles of various lengths in their cycle decomposition.

For example for \(S_2\), we have two elements and so we have two permutations

\(1 + 1\) \(id = (1)(2)\)
\(2\) \((1 \quad 2)\)

For \(S_3\),

\(1 + 1 + 1\) \(id = (1)(2)(3)\)
\(2 + 1\) \((1 \quad 2),(1 \quad 3),(2 \quad 3)\)
\(3\) \((1 \quad 2 \quad 3),(1 \quad 3 \quad 2)\)

For \(S_4\),

\(1 + 1 + 1 + 1\) \(id = (1)(2)(3)(4)\)
\(2 + 1 + 1\) \((1 \quad 2),(1 \quad 3),(1 \quad 4),(2 \quad 3),(2 \quad 4),(3 \quad 4)\)
\(2 + 2\) \((1 \quad 2)(3 \quad 4),(1 \quad 3)(2 \quad 4),(1 \quad 4)(2 \quad 3)\)
\(3 + 1\) \((1 \quad 2 \quad 3),(1 \quad 2 \quad 4)\),\((1 \quad 3 \quad 4),(2 \quad 3 \quad 4),(1 \quad 3 \quad 2)\),\((1 \quad 4 \quad 2),(1 \quad 4 \quad 3),(2 \quad 4 \quad 3)\)
\(4\) \((1 \quad 2 \quad 3 \quad 4),(1 \quad 2 \quad 4 \quad 3)\),\((1 \quad 3 \quad 2 \quad 4),(1 \quad 3 \quad 4 \quad 2)\),\((1 \quad 4 \quad 2 \quad 3),(1 \quad 4 \quad 3 \quad 2)\)


The Order of an Element

(Start of lecture 4). The first concept that we will talk about is the order of an element in a group.

Definition
Suppose we have a group \((G, \cdot)\) and let \(a \in G\). The order of \(a\) is the smallest positive integer \(n\) such that \(a^n = e\) (or infinite). \(\text{order}(a) \in \mathbf{N} \cup \{\infty\}\).


For example let \(\sigma = (1 \quad 2 \quad 3 \quad 4) \in S_5\) The order of \(\sigma\), \(\text{order}(\sigma)\) is \(4\). This is because it will take \(\sigma^4\) will finally get us back to the identity permutation. In fact that the order of a \(k-\)cycle is \(k\).

What about \(\tau = (1 \quad 2)(3 \quad 4 \quad 5)\)? \(\text{order}(\tau) = 6\) because we have to iterate the operation \(6\) times to get to the identity element. Specifically, we have two disjoint cycles and since they are disjoint, then they operate independently. So we need to find \(n\) such that both of the cycles will return to the identity permutation

$$ \begin{align*} (1 \quad 2)^n &= e \\ (3 \quad 4 \quad 5)^n &= e \end{align*} $$

This \(n\) must be then the least common multiple of \(2\) and \(3\) which is \(6\).

What about \(\nu = (1 \quad 2)(2 \quad 3 \quad 4)\)? Note here that the two cycles are not disjoint. It’s not clear here what it would be so drawing this permutation might make this very obvious.

[TODO:PIC]

From this we see that \(\text{order}(\nu) = 4\).


Parity of a Permutation

The second concept that we want to talk about is the parity of a permutation but first we’ll start with the following proposition.

Proposition
Every permutation of a finite set is equal to some product of transpositions (a transposition is 2-cycle) not necessarily disjoint.


For example we can write \((1 \quad 2 \quad 3 \quad 4)\) as \((1 \quad 2)(2 \quad 3)(3 \quad 4)\).

Next, we have the following proposition

Proposition
If \(\sigma\) is a permutation of a finite set and if \(\sigma = \tau_1\tau_2...\tau_k = \nu_1\nu_2...\nu_l\) where each of \(\tau_i\) and \(\nu_j\) are transpositions, then either \(k,l\) are both even, or are both odd. i.e. \((-1)^k = (-1)^l\)


Because of this we can classify permutations as even or odd. We also get the fact that composing two even permutations is another even permutations and composing an even permutation with an odd permutation is an odd permutation.

Proof (there is an alternative proof in the notes)
Define a function \(sgn: S_n \rightarrow \{\pm 1\}\) such that

  1. \(sgn(id) = +1\)
  2. \(sgn(\sigma \circ \tau) = sgn(\sigma)sgn(\tau)\)
  3. If \(\tau\) is a transposition, then \(sgn(\tau) = -1\)

So now given a permutation \(\sigma \in S_n\), there is a corresponding permutation matrix \(A_{\sigma} \in GL_{n}(\mathbf{R})\). \(A_{\sigma}\) has the standard basis vectors but permuted according to the permutation \(\sigma\). For example

$$ \begin{align*} A_{(1 \quad 2 \quad 3)} &= \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \end{align*} $$

So

$$ \begin{align*} A_{\sigma} &= \begin{pmatrix} e_{\sigma(1)} & e_{\sigma(2)} & ... & e_{\sigma(n)} \end{pmatrix} \end{align*} $$

where \(e_{\sigma(k)}\) is the standard column vector \(e_k\) permuted according to \(\sigma(k)\).

The permutation matrix \(A_{\sigma}\) is useful in that left multiplication by \(A_{\sigma}\) permutes the subset \(\{e_1,...,e_n\} \in \mathbf{R}^n\) according to \(\sigma\). So

$$ \begin{align*} A_{\sigma}e_k = e_{\sigma(k)} \end{align*} $$

This actually leads to a formula

$$ \begin{align*} A_{\sigma}A_{\tau} = A_{\sigma \circ \tau} \end{align*} $$

This is because

$$ \begin{align*} A_{\sigma}A_{\tau}e_k = A_{\sigma}e_{\tau(k)} = e_{\sigma(\tau(k))} \leftrightarrow A_{\sigma \circ \tau}e_k = e_{(\sigma \circ \tau)(k)} \end{align*} $$

So now define: \(sgn(\sigma) = \det(A_{\sigma})\) where \(sgn: S_n \rightarrow \{\pm 1\}\). This function satisfies the three properties we defined for the \(sgn\) function above.

  1. \(sgn(id) = +1\). This is true because the permutation matrix for the identity permutation is the identity matrix.
  2. \(sgn(\sigma \circ \tau) = sgn(\sigma)sgn(\tau)\). This follows from the product property of the determinant. \(\det(AB) = \det(A)\det(B)\).
  3. If \(\tau\) is a transposition, then \(sgn(\tau) = -1\). This also follows from the fact that interchanging any two columns from a matrix results in switching the sign of the determinant.




References