Introduction

Abstract Algebra lets us examine structures which allow for algebraic manipulations of the types we’ve used in high school. As an example, we have Fields. It’s a set with operations addition, subtraction, multiplication and division that satisfy a few rules. An example of a field is the field of real numbers \(\mathbf{R}\) or the field of complex numbers \(\mathbf{C}\). We also have the field of rational numbers \(\mathbf{Q}\). Or \(\mathbf{Z}_p\) which is a finite field of integers modulo some prime \(p\). It is finite with \(p\) elements.

Another example of important structures are Rings. Here we have the operations addition, subtraction and multiplication. The first example of a ring is \(\mathbf{Z}\). Another example of a ring is a polynomial ring in one variable over \(\mathbf{R}\), \(\mathbf{R}[x]\). The set of all square matrices. \(M_{n \times n}(\mathbf{R})\) is also another example. This example is non-commutative.


Another structure is a Group. It is a set with one operation usually called “multiplication”. One example is the set of real numbers with just addition. Another example is \((\mathbf{R}^{x})\) (the set of real numbers with zero removed, \(\mathbf{R} - \{0\}\) along with multiplication. \(GL(n,\mathbf{R})\), the set of invertible matrices with multiplication is another example of a Group. This is an example of a non-abelian or non-commutative group.

One additional structure that comes up is a Monoid. These are sets with one operation but you don’t have to have inverses like Groups. So \(\mathbf{R}\) with multiplication is not a group because it includes zero and zero doesn’t have an inverse but this set is a Monoid.


Groups and Symmetries

From the book, a symmetry is an undetectable motion. An object is symmetric if it has symmetries. Take an equilateral triangle.

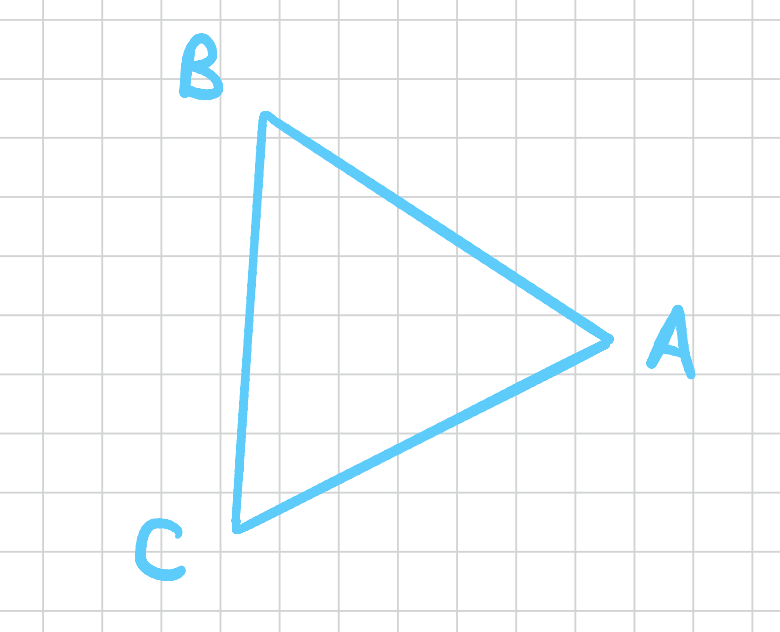
What are the symmetries of this triangle? We want to rotate the triangle in such a way that we won’t tell if it was rotated. For example, if we rotate this triangle by \(120\) degrees counter clockwise, then we’ll get a triangle in the same exact orientation. We label this rotation with \(r_1\). Note here that the labels on the vertices are used to illustrate that we indeed have rotated the triangle. They are a visual aid.

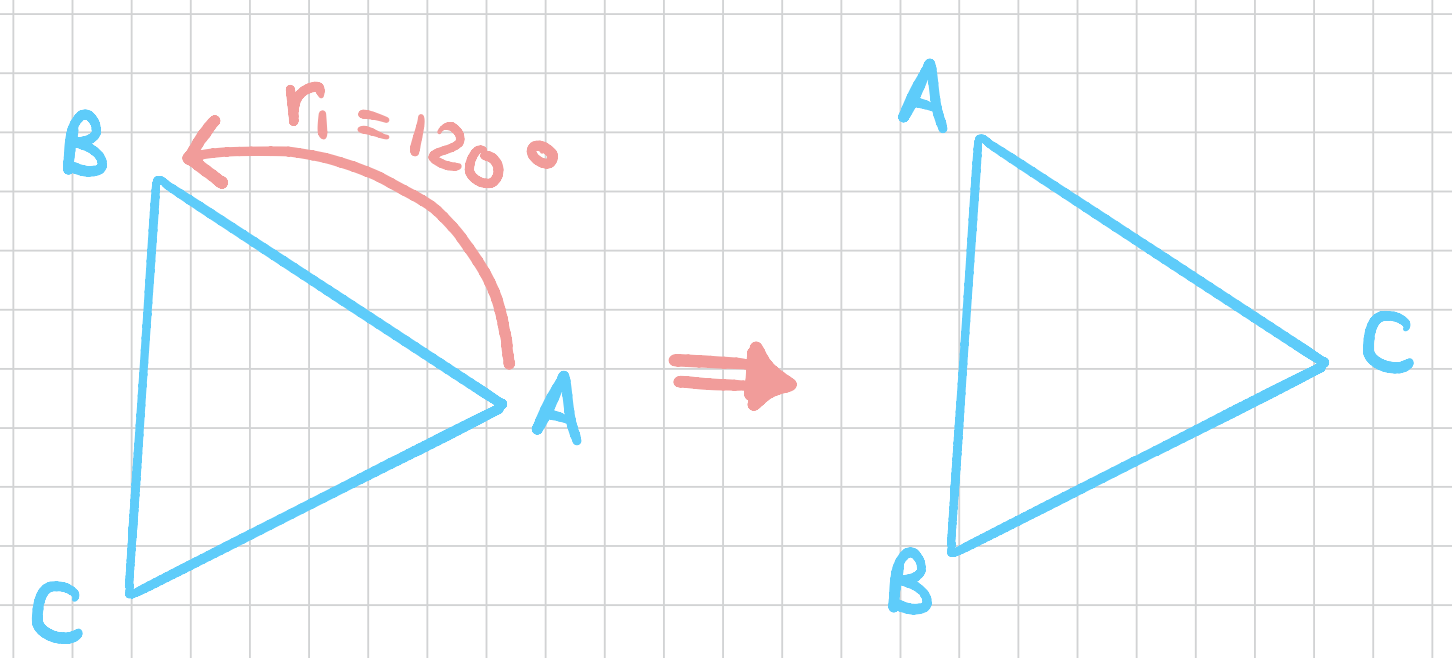
We can also rotate this triangle \(120\) degrees clockwise to get the following \(r_2\) rotation.

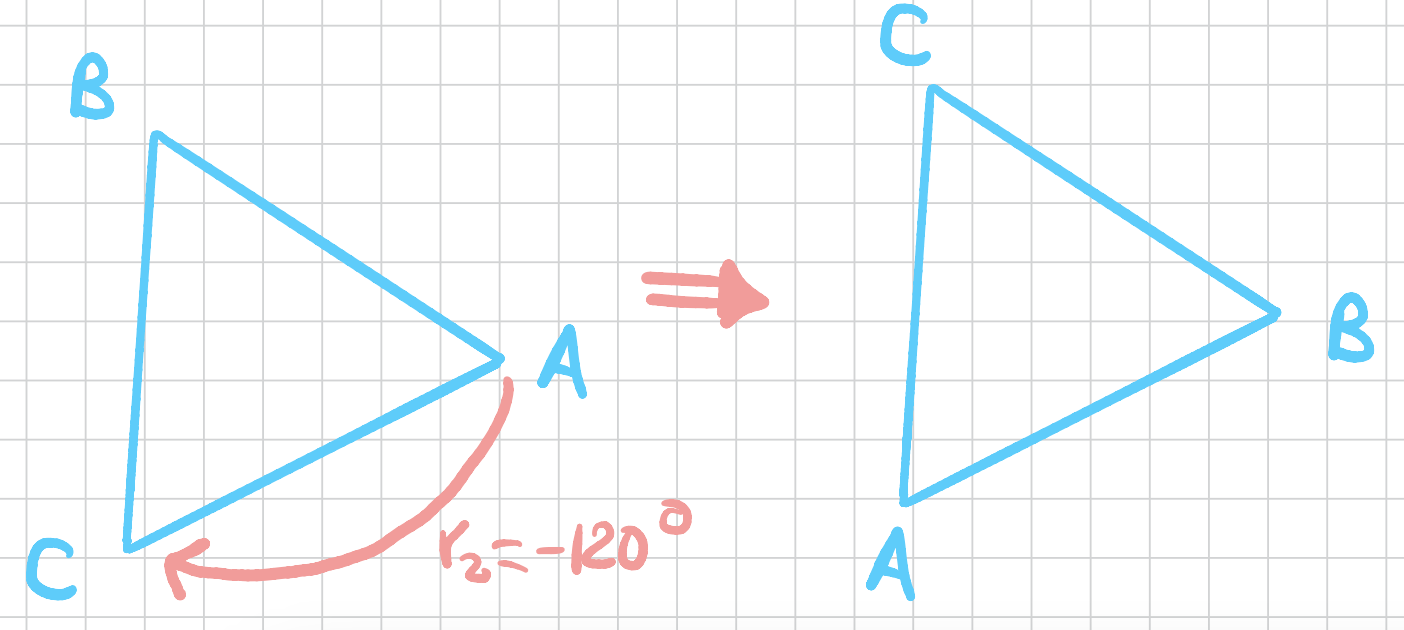
Are there more rotations? Yes, consider the rotation around the axis that goes through the vertex \(A\) by 180 degrees so essentially it’s a flip around that axis.

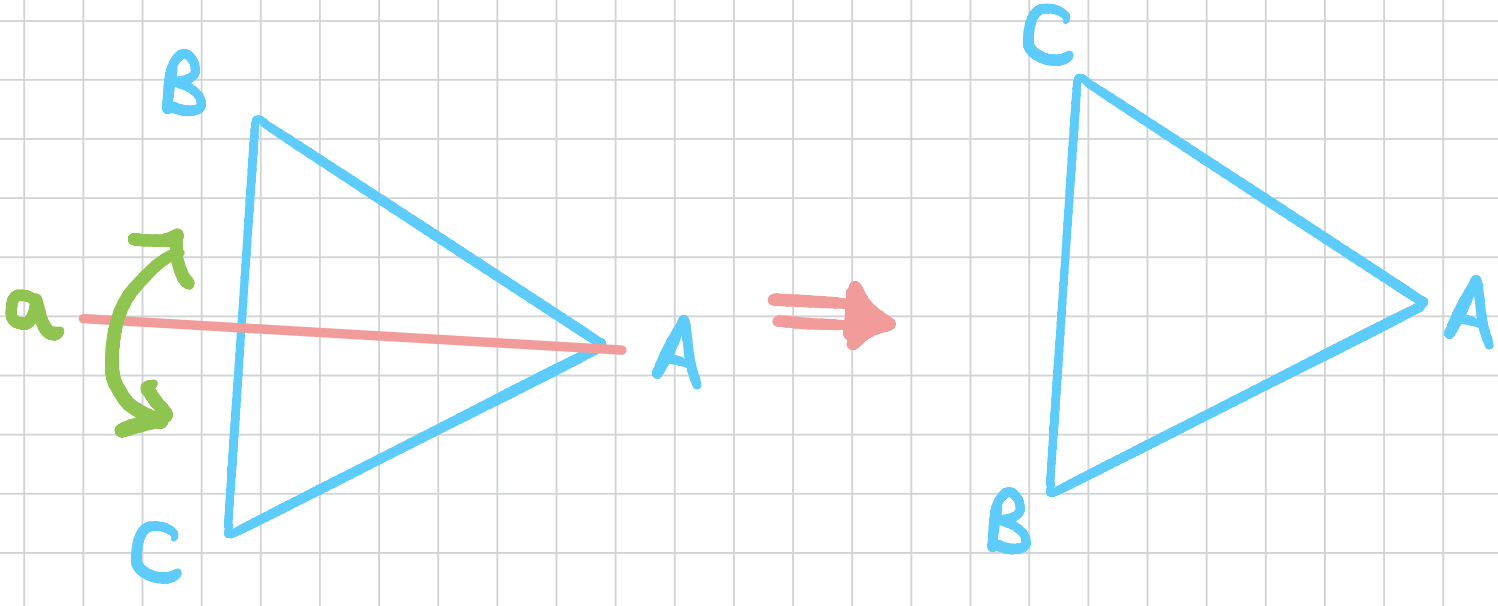
Similarly, we can do a flip around the axis that goes through the vertex \(B\) and a flip around the axis that goes through the vertex \(C\).

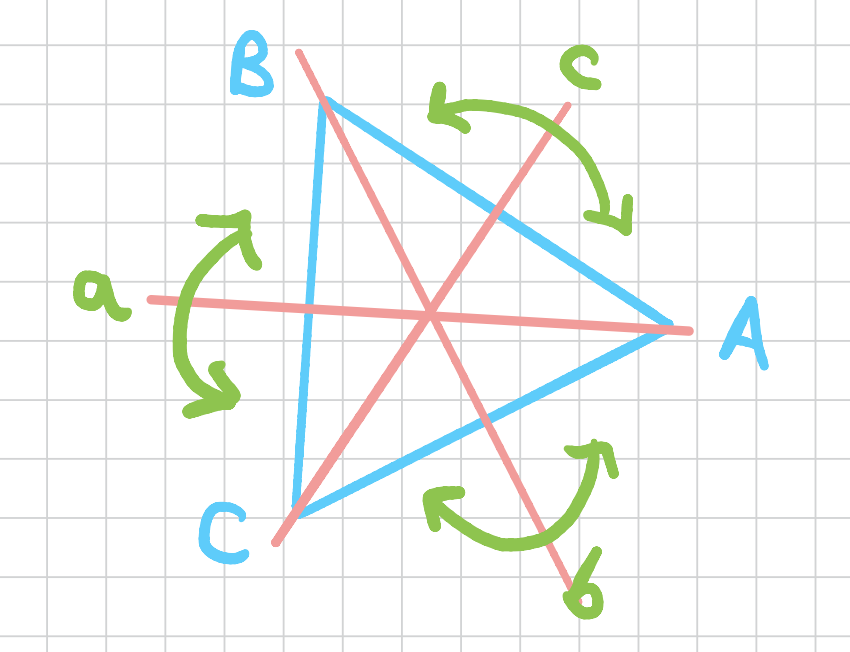
So now we have \(5\) symmetries total. Is that all? No, We have one more symmetry representing the identity symmetry \(e\) that does nothing. So the set of symmetries are then

$$ \begin{align*} G = \{e, r_1, r_2, a, b, c\} \end{align*} $$



Can We Compose Symmetries?

Can we compose symmetries? Yes, in fact we’ll equip the group above with the operation compose. This means that for any \(x, y \in G\), \(xy\) means that we need to apply the rotation \(y\) first and then apply the rotation \(x\). Since we have \(6\) elements in \(G\), then we have \(36\) ways of composing these elements.

For example composing \(r_1\) with \(r_1\) again results in the rotation \(r_2\) so \(r_1r_1 = r_2\).

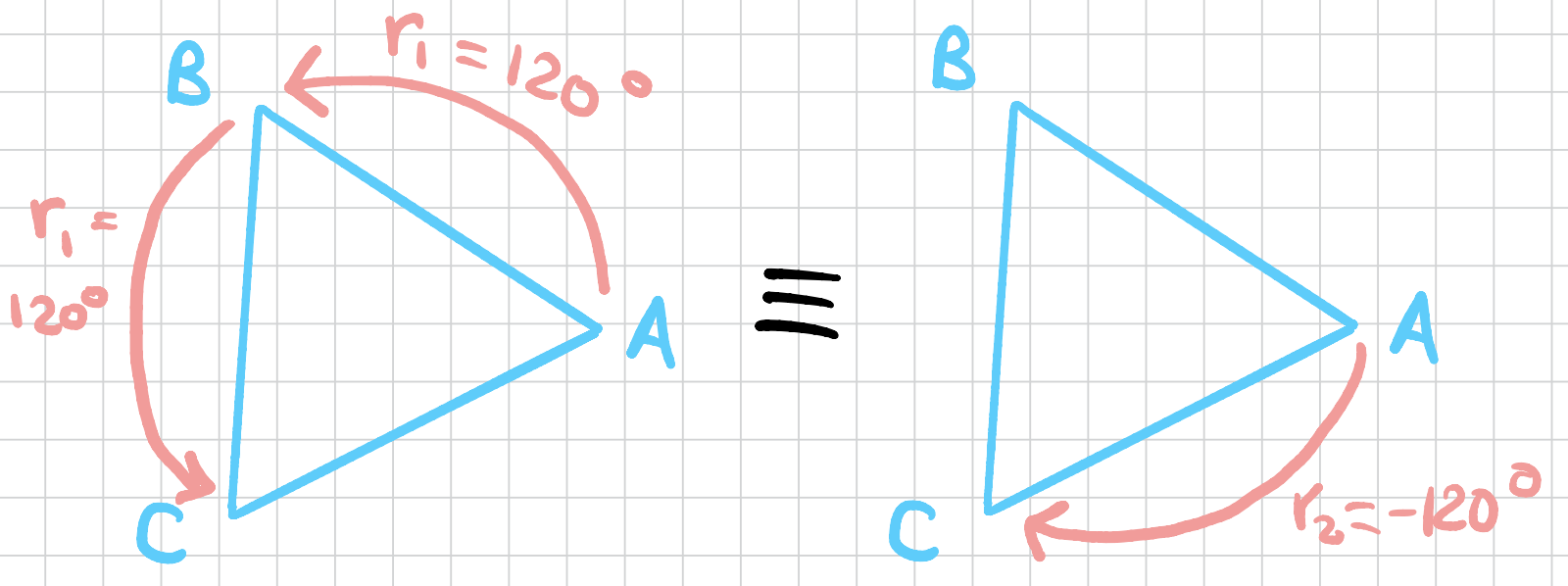
And if we compose \(r_1\) with \(r_2\), then we’ll get the identity rotation so \(r_1r_2 = e\).

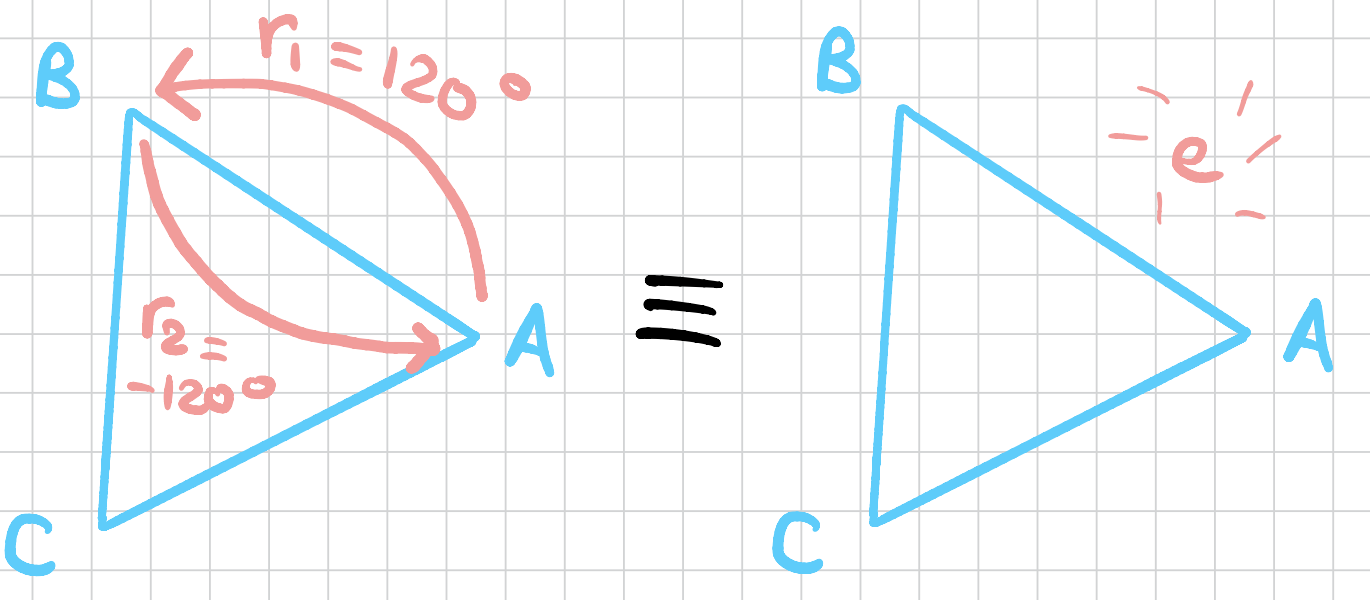
In fact since \(r_1r_1 = r_2\) and \(r_1r_2 = e\), we’ll change the notation to a much simpler notation. Let \(r_1 = r\). Then, \(r_2 = r_1r_1 = rr = r^2\). So now we can fill these in a table as follows

\(e\) \(r\) \(r^2\) \(a\) \(b\) \(c\)
\(e\) \(e\) \(r\) \(r^2\) \(a\) \(b\) \(c\)
\(r\) \(r\) \(r^2\) \(e\) \(\) \(\) \(\)
\(r^2\) \(r^2\) \(e\) \(r\) \(\) \(\) \(\)
\(a\) \(a\) \(\) \(\) \(\) \(\) \(\)
\(b\) \(b\) \(\) \(\) \(\) \(\) \(\)
\(c\) \(c\) \(\) \(\) \(\) \(\) \(\)


So far so good. What about composing the flips around the axes? For example composing \(a\) with \(b\). What would that do? For starters, note that each flip is a \(180\) degrees flip. So if you compose ANY two flips, we’ll be back to the same face we started with. This means that any two flips will be equivalent to \(e, r\) or \(r^2\). For example, if we apply \(a\) and then apply \(b\), we’ll get

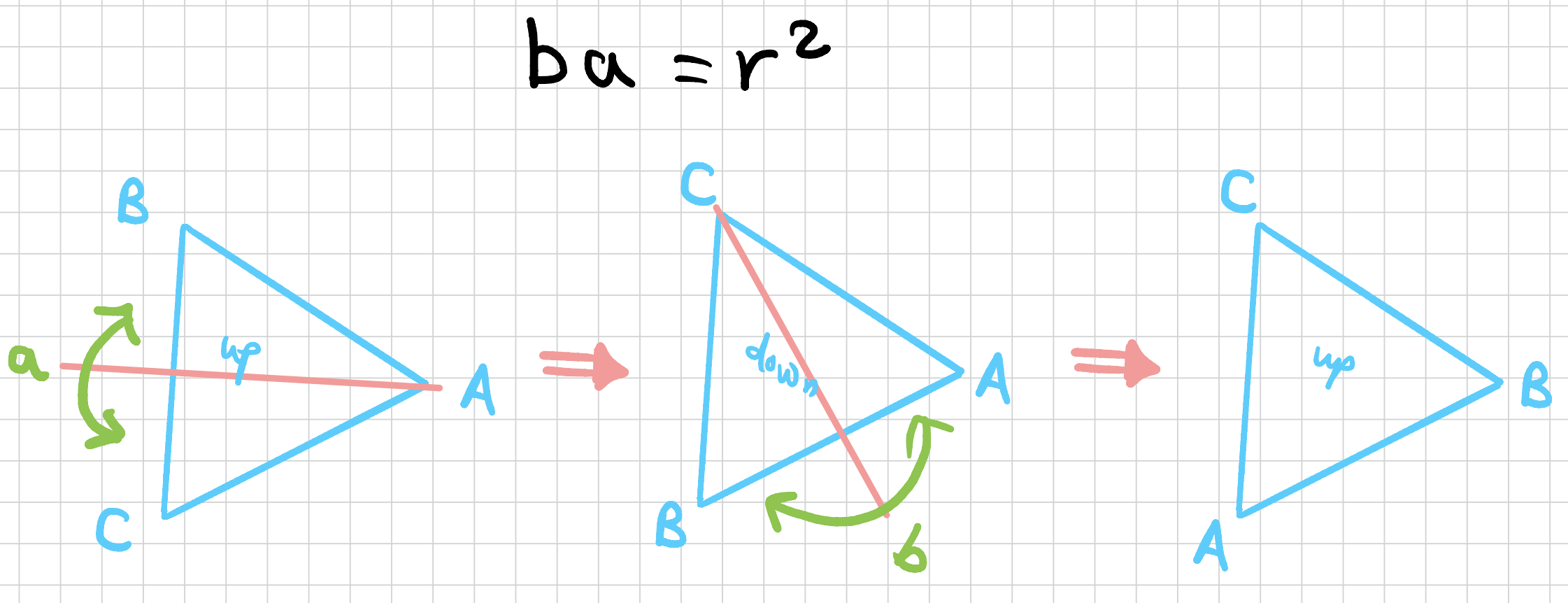
Note here that when did the second flip, we still rotated through the \(b\) access which now goes through vertex \(C\) instead. Physically the axis will still be in the same position. So we see above doing two flips \(a\), then around \(b\) is equivalent to applying two rotations so \(ba = r^2\).

What about two flips of the same type? What happens if you apply \(a\) and then again flip it around that same access? We’ll get the identity rotation since we just go back to the same exact orientation. Applying this same logic on the rest of flips, we can fill that forth quadrant of the table which are all about compositions of flips.

\(e\) \(r\) \(r^2\) \(a\) \(b\) \(c\)
\(e\) \(e\) \(r\) \(r^2\) \(a\) \(b\) \(c\)
\(r\) \(r\) \(r^2\) \(e\) \(\) \(\) \(\)
\(r^2\) \(r^2\) \(e\) \(r\) \(\) \(\) \(\)
\(a\) \(a\) \(\) \(\) \(e\) \(r\) \(r^2\)
\(b\) \(b\) \(\) \(\) \(r^2\) \(e\) \(r\)
\(c\) \(c\) \(\) \(\) \(r\) \(r^2\) \(e\)


Second and Third Quadrants

What about applying a rotation \(r\) followed by a flip \(a\)? What is \(ar\)? We apply a rotation so we move \(120\) degrees anti-clockwise and then we do an \(a\) flip which is now going to be through the \(C\) vertex. The triangle will now be faced down which is equivalent to applying a single flip. Comparing the vertices in the original triangle and the outcome, we see that \(B\) is fixed while \(A\) and \(C\) have switched. This means that this is a flip around the \(b\) access.

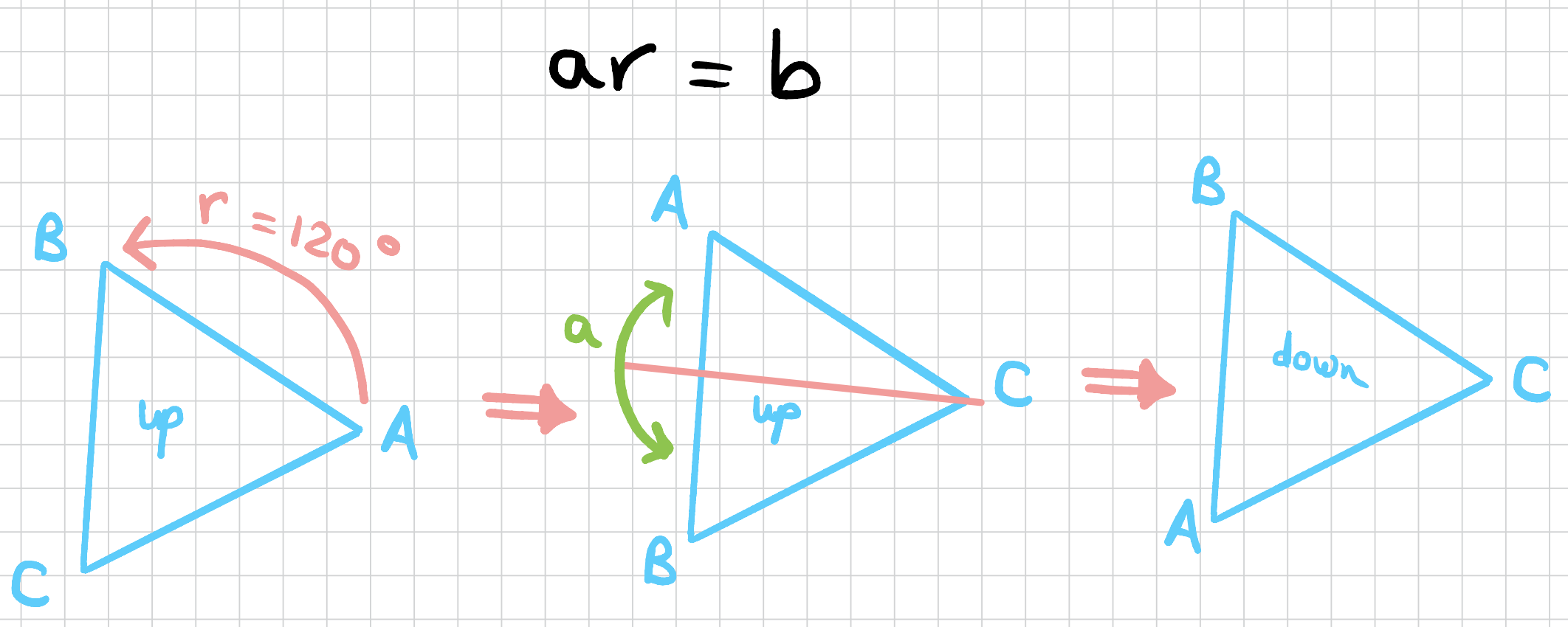
\(e\) \(r\) \(r^2\) \(a\) \(b\) \(c\)
\(e\) \(e\) \(r\) \(r^2\) \(a\) \(b\) \(c\)
\(r\) \(r\) \(r^2\) \(e\) \(c\) \(a\) \(b\)
\(r^2\) \(r^2\) \(e\) \(r\) \(b\) \(c\) \(a\)
\(a\) \(a\) \(b\) \(c\) \(e\) \(r\) \(r^2\)
\(b\) \(b\) \(c\) \(a\) \(r^2\) \(e\) \(r\)
\(c\) \(c\) \(a\) \(b\) \(r\) \(r^2\) \(e\)

We notice that each row has each rotation appearing exactly once and it’s the same for each column. Notice also that composition is not commutative above. So \(ar \neq ra\).


Matrix Representation of Symmetries

We can actually represent these symmetries by matrices. For example, the following matrix will represent a \(120\) degrees rotation around the \(z-\) axis

$$ \begin{align*} r(x,y,z) &= \begin{pmatrix} \cos\frac{2\pi}{3} & - \sin\frac{2\pi}{3} & 0 \\ \sin\frac{2\pi}{3} & + \cos\frac{2\pi}{3} & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{align*} $$

or we can do the \(a\) flip so a \(180\) degree flip around the \(x\)-axis.

$$ \begin{align*} a(x,y,z) &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 0 \end{pmatrix} \end{align*} $$

What about something more complex? like \(ra\) which is equal to \(c\) using the multiplication table above. This will be

$$ \begin{align*} c(x,y,z) &= ra(x,y,z) \\ &= \begin{pmatrix} \cos\frac{2\pi}{3} & - \sin\frac{2\pi}{3} & 0 \\ \sin\frac{2\pi}{3} & + \cos\frac{2\pi}{3} & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 0 \end{pmatrix} \\ &= \begin{pmatrix} \cos\frac{2\pi}{3} & \sin\frac{2\pi}{3} & 0 \\ \sin\frac{2\pi}{3} & - \cos\frac{2\pi}{3} & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{align*} $$



Symmetries of the Rectangle

How many symmetries does the rectangle have?

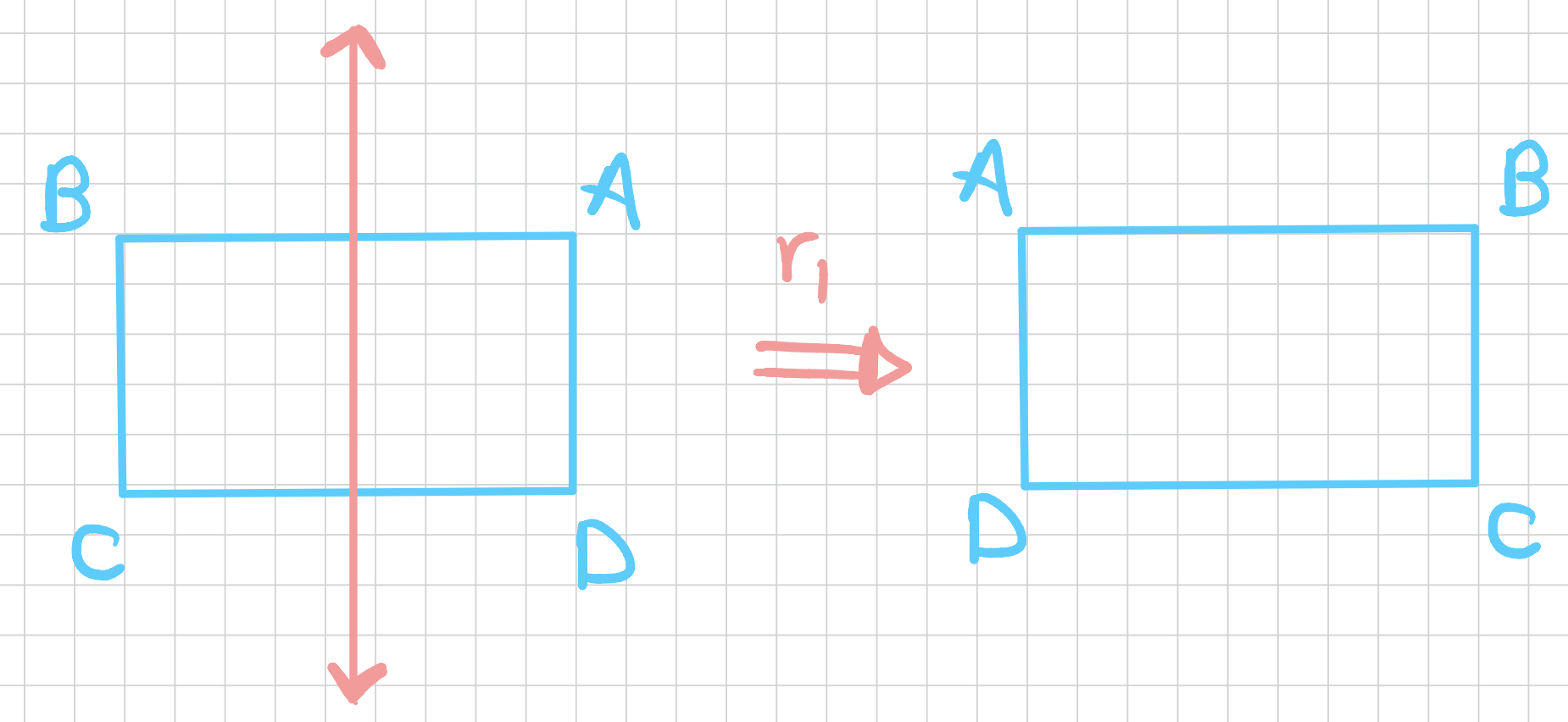
We can have a rotation \(r_1\) around the \(y-\)axis as follows

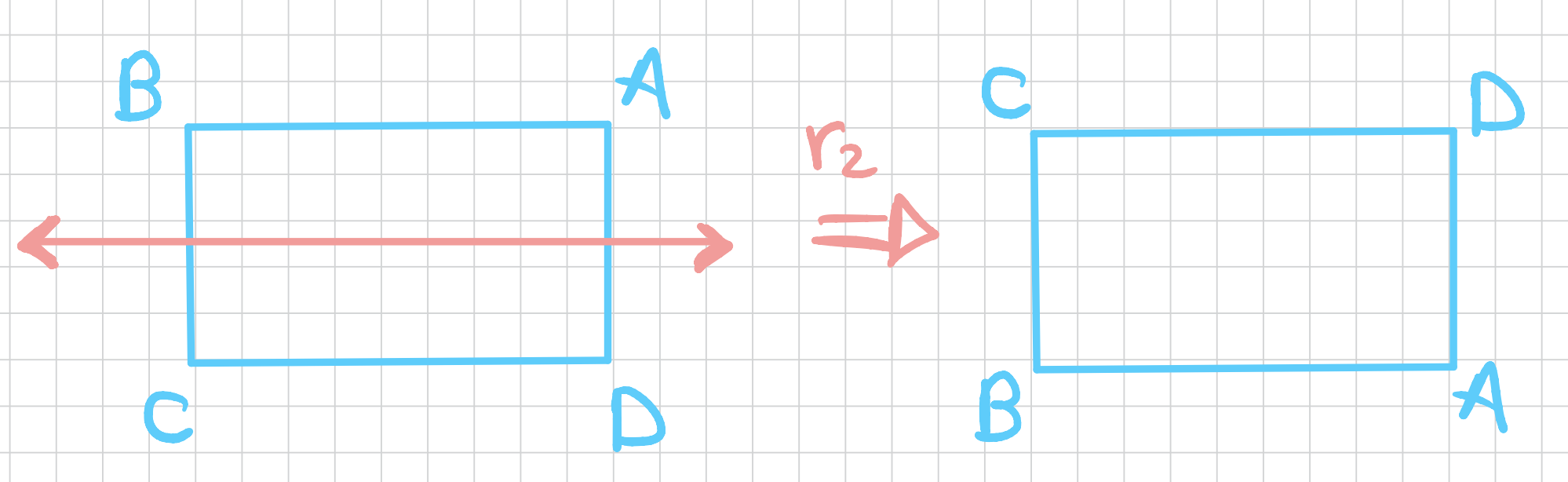
We can also have a rotation \(r_2\) around the \(x-\)axis

Finally, we have one more rotation \(r_3\) around the \(z-\)axis. (the axis coming off the screen toward us from the centroid of the face.)

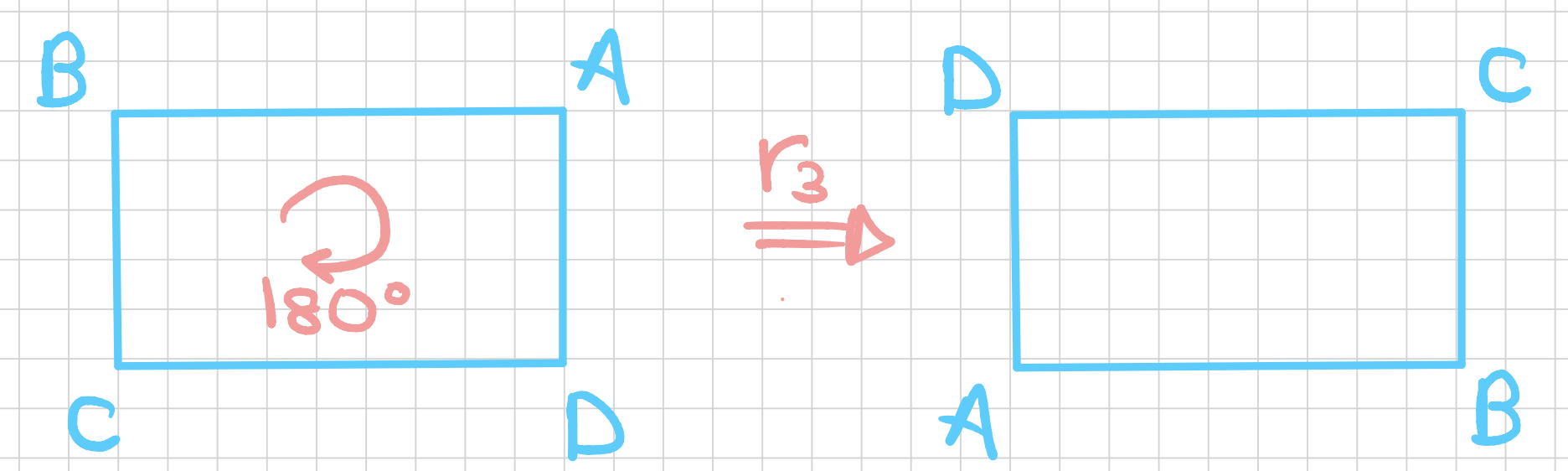
So we have four rotations which make the following group

$$ \begin{align*} G = \{e, r_1, r_2, r_3\} \end{align*} $$

One thing to notice here that for any rotation in \(G\), if you apply it twice, you’ll get the identity rotation. So each rotation has an order \(2\). The multiplication table for the symmetries of the rectangle is as follows

\(e\) \(r_1\) \(r_2\) \(r_3\)
\(e\) \(e\) \(r_1\) \(r_2\) \(r_3\)
\(r_1\) \(r_1\) \(r_2\) \(r_3\) \(e\)
\(r_2\) \(r_2\) \(r_3\) \(e\) \(r_1\)
\(r_3\) \(r_3\) \(e\) \(r_1\) \(r_2\)




Symmetries of the Square

What about the symmetries of the square? There are eight of them. First we consider the axis coming through the centroid of the face toward us. There are three rotations around this axis.

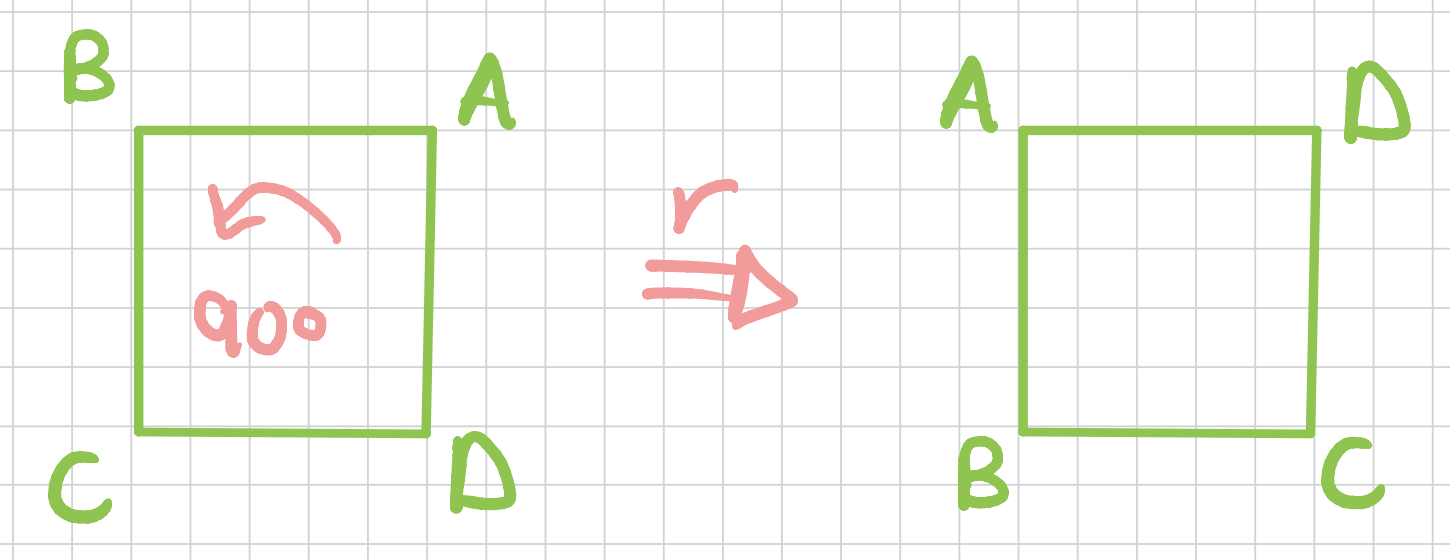
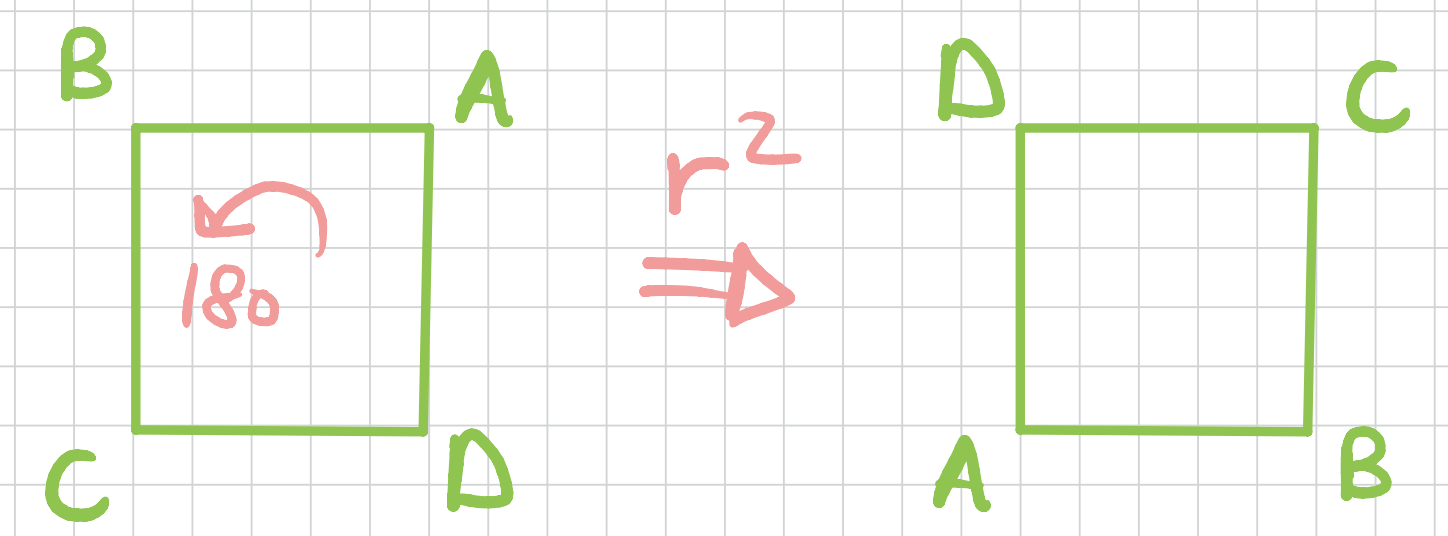
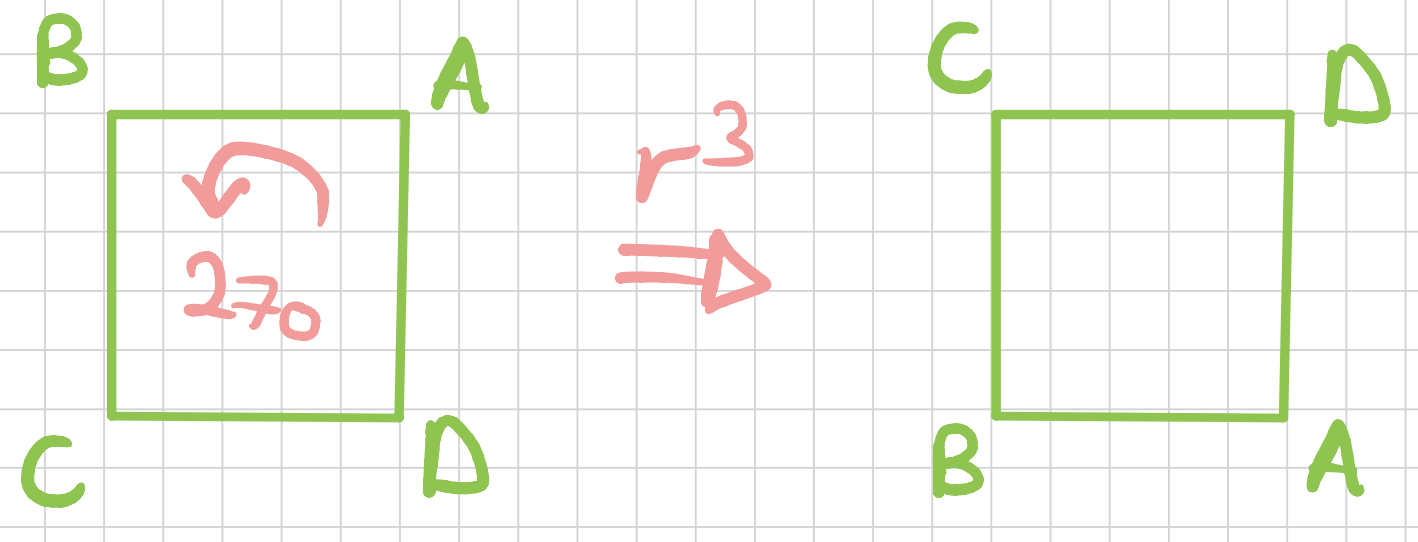
Next, we can consider the \(x-\)axis or the axis coming through the center of the edges. We can do a \(180\) degrees rotation around this access (a flip). Call this one \(a\).

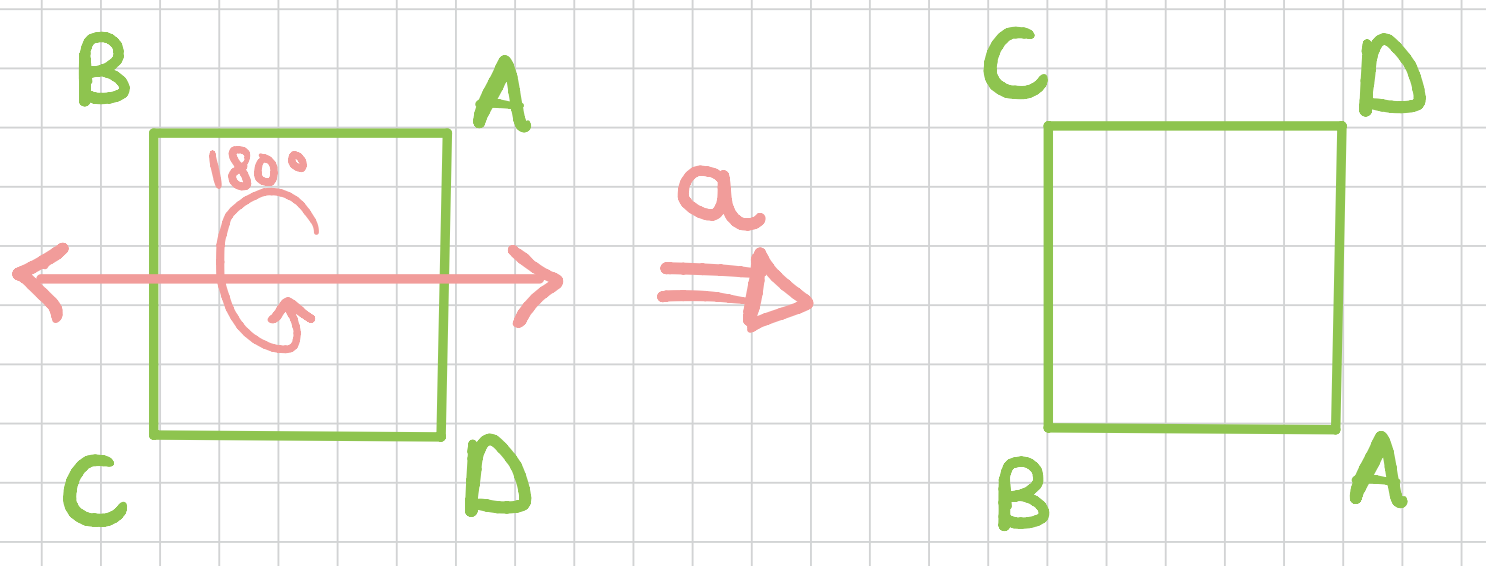
Similarly, we can do one around the \(y-\)axis.

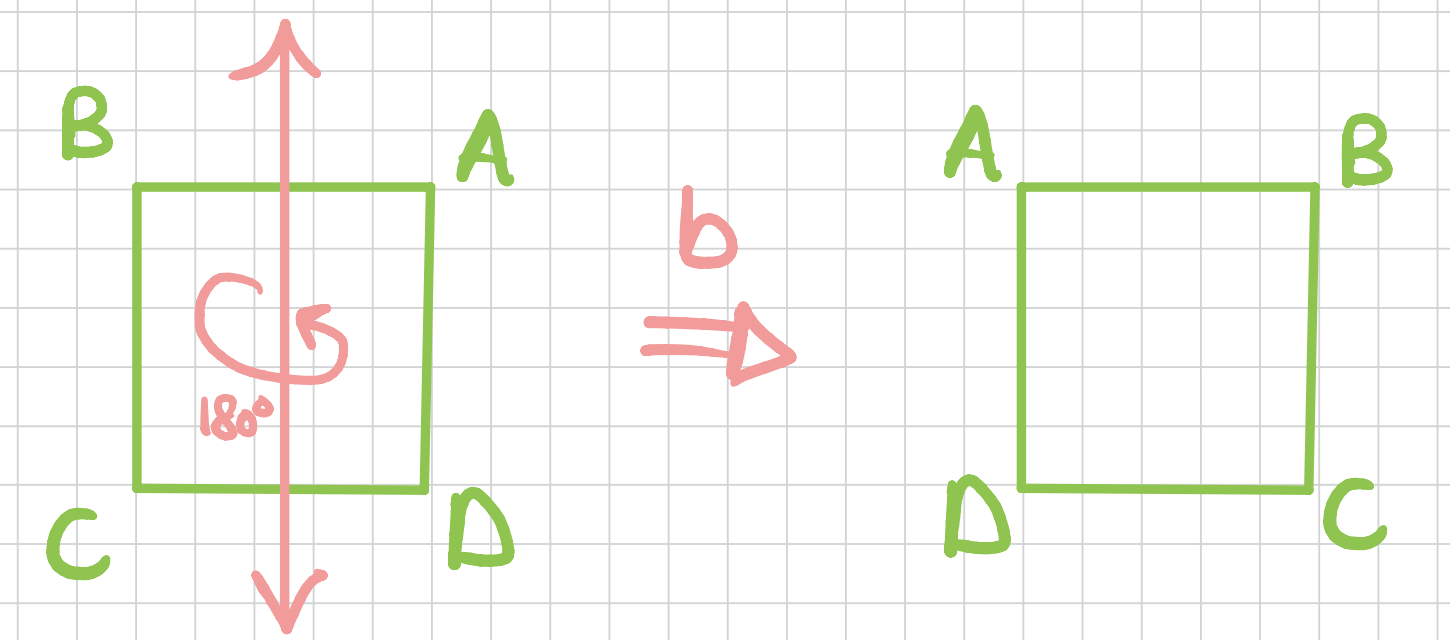
And then two more through the diagonals of the square.

$$ \begin{align*} G = \{e, r, r^2, r^3, a, b, c, d\} \end{align*} $$


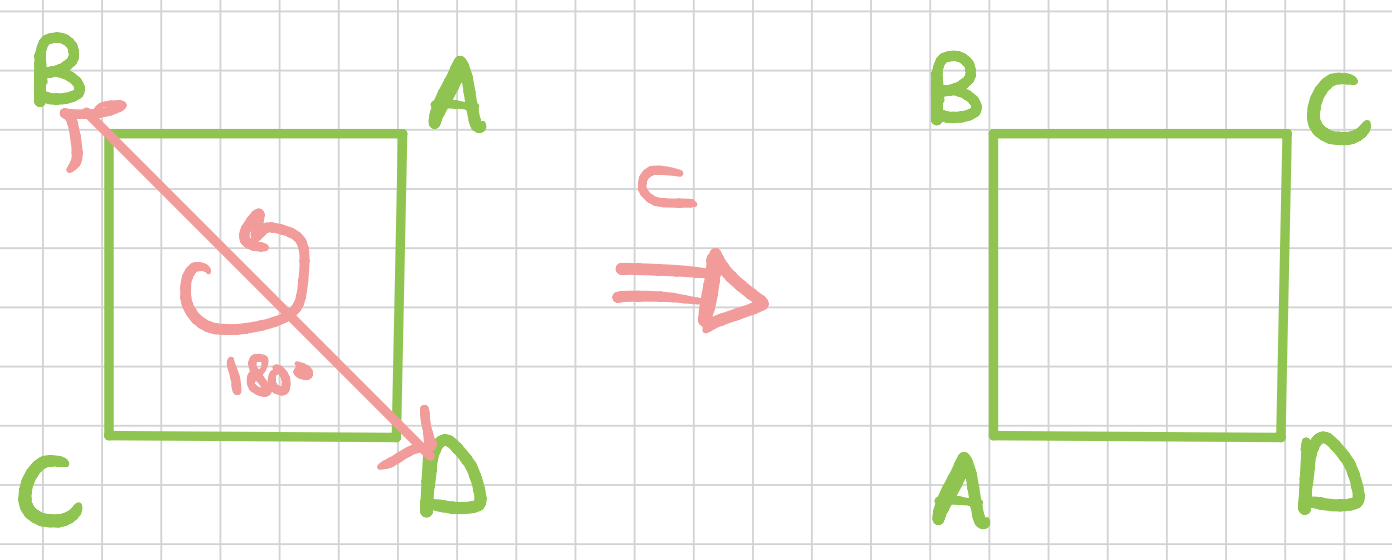
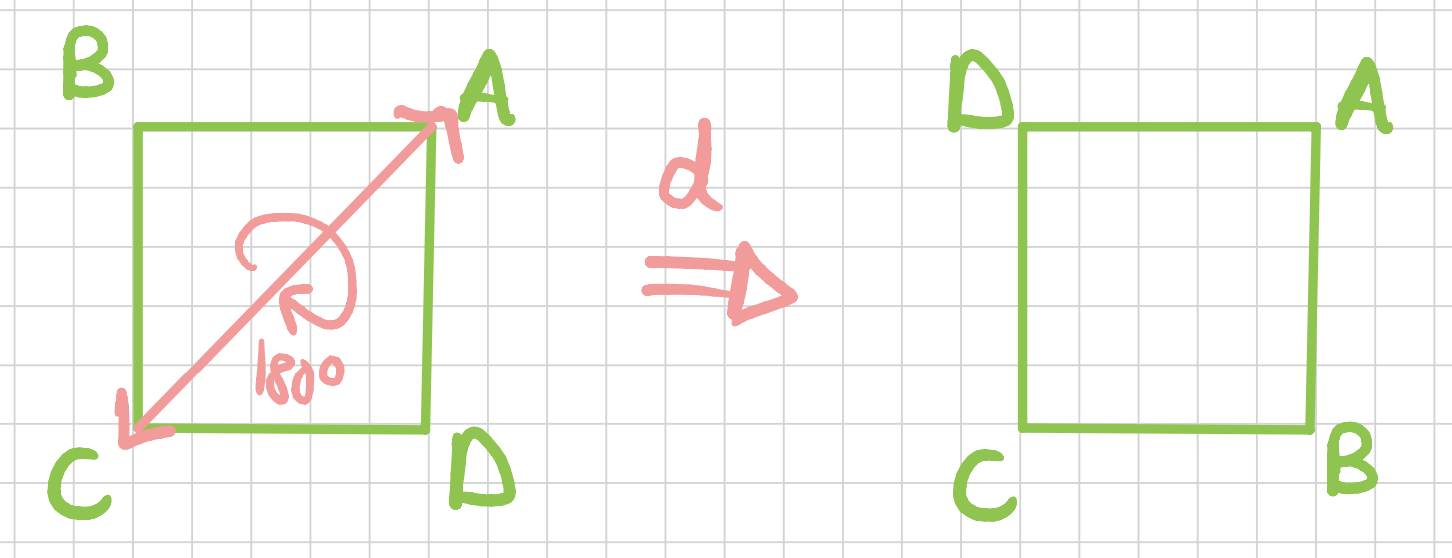
What about the cube? How many symmetries does it have? it has 24 symmetries!


References