My first solution was just to sum the numbers across the diagonals after breaking them into 4 parts.
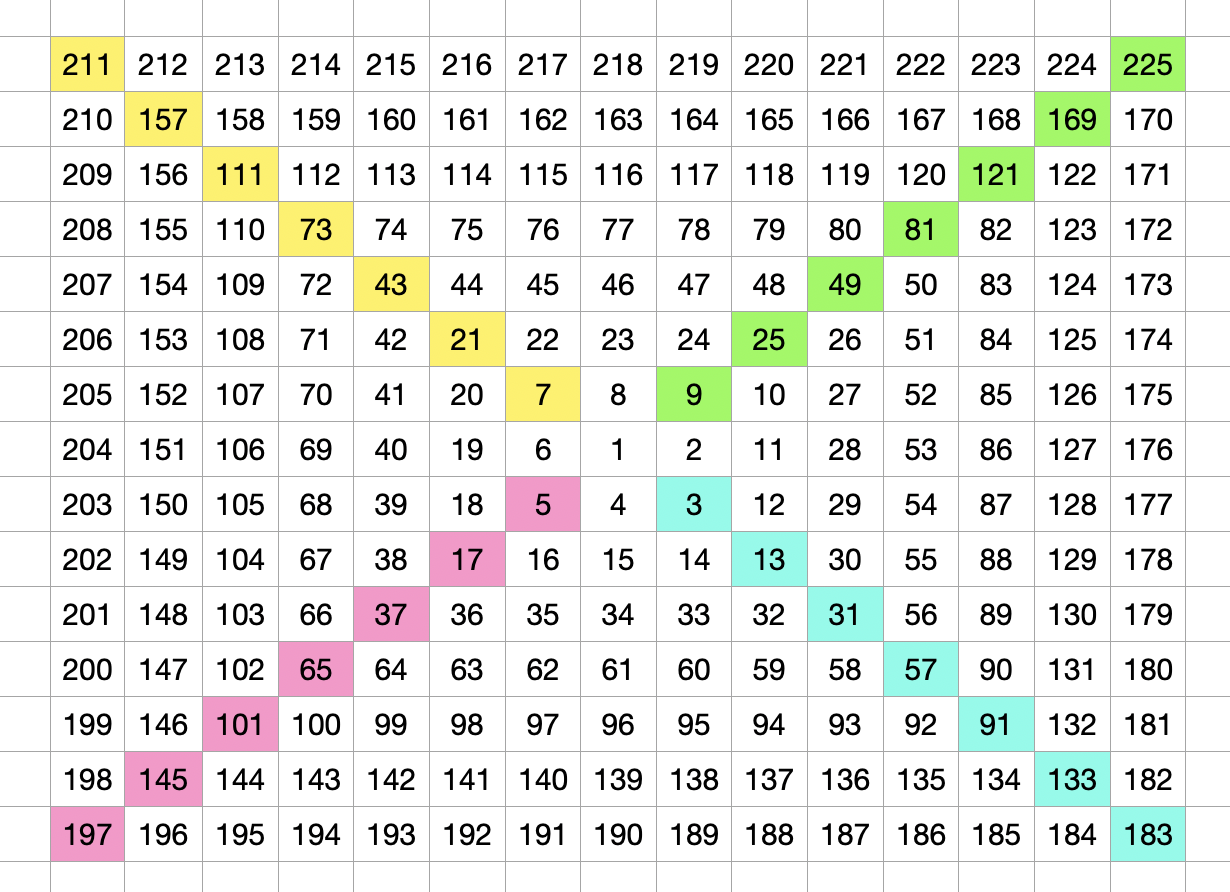
We can come up with a formula for the yellow cells for example by observing that the difference between the cells follow a pattern.
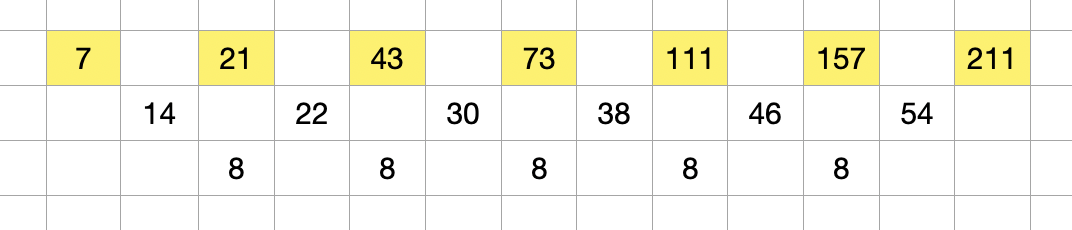
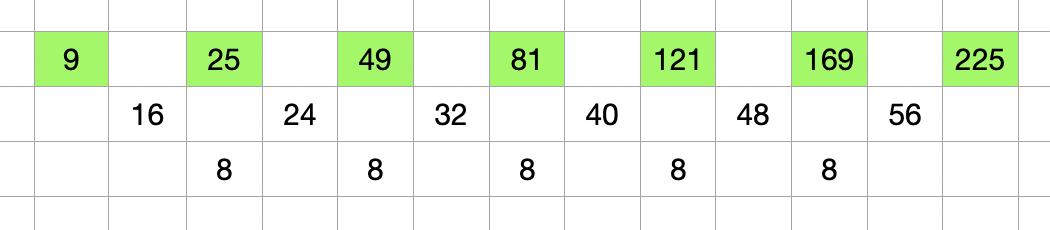
You can see above that the difference between the cells keeps increasing by 8 each time we move up. Similarly, we can find that the other 3 parts follow a similar pattern. For example, we can see that the difference between the cells below also increases by 8. The only difference between the green cells and the yellow cells is that the initial difference here is 9 while it was 7 for the yellow cells.
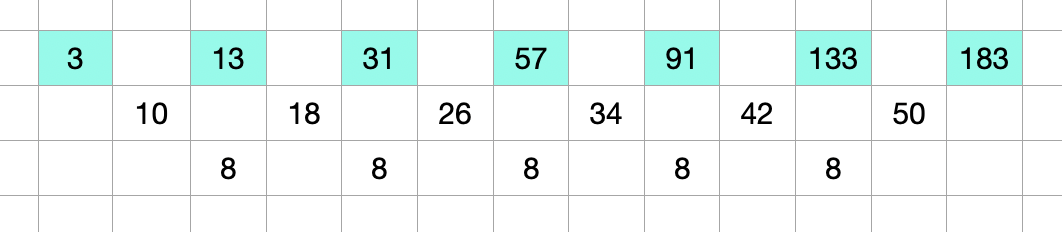
Similarly, the difference between the blue cells also increase by 8 but the initial difference is 3 here.
So we can come up with the following function that takes the initial cell value and the initial difference and then returns the total sum. Since the grid is \(1001 \times 10001\), then each quadrant will contain 500 cells.
int sum_quadrant(int cell, int diff) {
int add = 8, sum = 0;
for (int i = 1; i <= 500; i++) {
sum += cell; // add the cell value
cell += diff; // cell value will increase by the diff
diff += add; // the diff will increase by 8 each iteration
}
return sum;
}
We now can use the above method to print the total.
long total_sum = 0;
total_sum += sum_quadrant(7, 14); // Top Left Diagonal
total_sum += sum_quadrant(9, 16); // Top Right Diagonal
total_sum += sum_quadrant(3, 10); // Bottom Right Diagonal
total_sum += sum_quadrant(5, 12); // Bottom Left Diagonal
printf("%ld\n", total_sum + 1);Closed Formula
Of course my naive solution was too basic and it seems that there is a closed formula for this … I have yet to do it! [TODO]