Notes
Cantor published this proof in 1874! It’s one of the most beautiful proofs I have ever seen.
Proof
Assume for the sake of contradiction that (0,1) is countable. This means that there exists a function \(f: \mathbb{N} \rightarrow (0,1)\) that is 1-1 and onto. So for each \(m \in \mathbb{N}\), \(f(m)\) is a real number between 0 and 1. We’ll represent this number using the decimal notation. So for each \(m, n \in mathbf{N}, a_{mn}\) is the digit from the set {0,1,2,…,9} that represents that \(n\)th digit in the digital representation of \(f(m)\),
We can summarize the 1-1 correspondance between \(\mathbb{N}\) and \((0,1)\) in the following table,
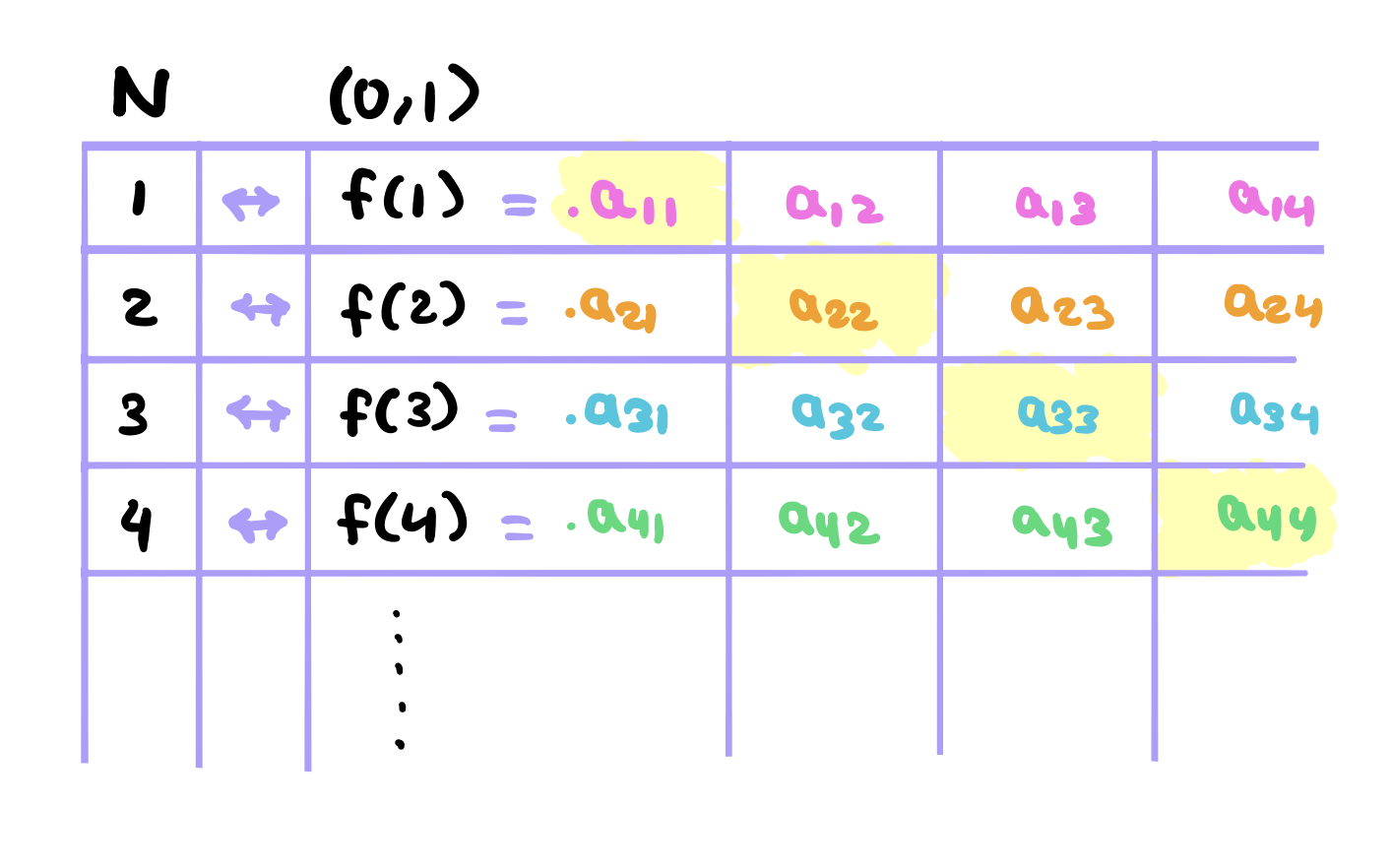
This table by our assumption should have every number in the interval \((0,1)\). Now, we are going to construct construct a real number \(x = .x_1x_2x_3.... \in (0,1)\) by considering only the diagonal digits in the above table.
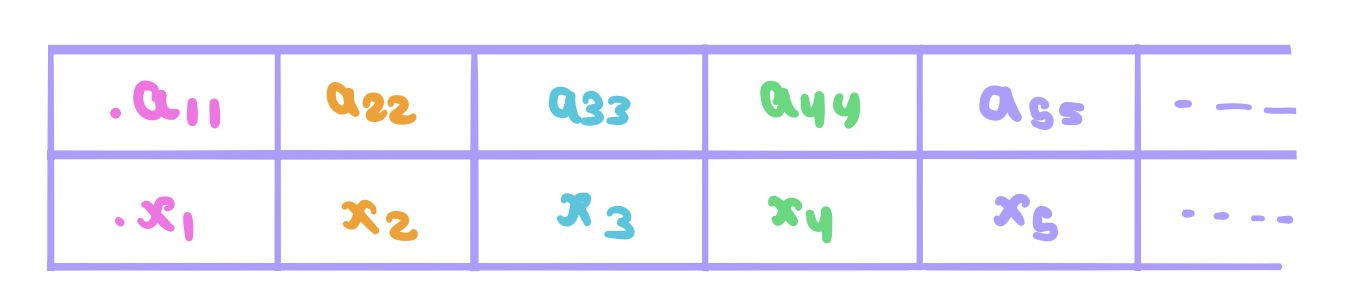
The neat trick though is that we are going to select a different digit for \(x_n\) than what we have in \(a_{nn}\). So, for the digit \(x_1\), we are going to select something different than \(a_{11}\), \(x_2\) will be different than \(a_{22}\) and so on. In particular, we are going to use the following rule:
The choice of the numbers 2 and 3 is made to avoid selecting a number that is equal to 0.999999999. So the selection of 2 and 3 is not really important here. We could make a different selection if we want as long as we don’t select 9. The important point to stress here is that we’re choosing a different digit than what’s on the diagonal. So if the diagonal digits were \(.a_{11}a_{22}a_{33}.... = 0.5242\), the number we select will be \(.x_{11}x_{22}x_{33}....=0.2323\)
The claim is that this number \(x\) is not in the table above! to see why, notice that \(x \neq f(1)\) because the digits \(x_1\) and \(a_{11}\) are not equal by construction. Similarly, \(x \neq f(2)\) because the digits \(x_2\) and \(a_{22}\) are different by construction. In fact, for any number in the table \(f(m)\) it can’t equal \(x\) because the digits \(x_{n}\) and \(a_{nn}\) will never be equal by our construction. Therefore, our assumption is incorrect and \((0,1)\) is uncountable.
\(\blacksquare\)
References: