The Nested Internval Property
For each \(n \in \mathbb{N}\), assume we are given a closed bounded interval \(I_n = [a_n, b_n] = \{x \in \mathbb{R}: a_n \leq x \leq b_n\}\). Also assume that \(I_n\) contains \(I_{n+1}\). That is, we have a nested sequence of closed intervels as follows $$ \begin{align*} I_1 \supseteq I_2 \supseteq I_3 \supseteq I_4 ... \end{align*} $$ Moreover, if the lengths of these intervals satisfy \(|I_n| \rightarrow 0\) as \(n \rightarrow \infty\), then the intersection of all of these sequences is not empty. That is $$ \begin{align*} \bigcap_{n=1}^{\infty} I_n \neq \emptyset. \end{align*} $$ Moreover, the intersection contains only a single point.

Discussion

This result depends on the axiom of completeness (recall that MCT depends on it) and it’s another way of showing that \(\mathbb{R}\) is complete and has no holes because even if we have an infinite number of these nested intervals, their intersection will not be empty. Why another result? Because it might be more intuitive think about a never ending nested intervals without ever being empty than thinking about always having a least upper bound for bounded sets.

Proof (Introduction by Real Analysis by William Wade)

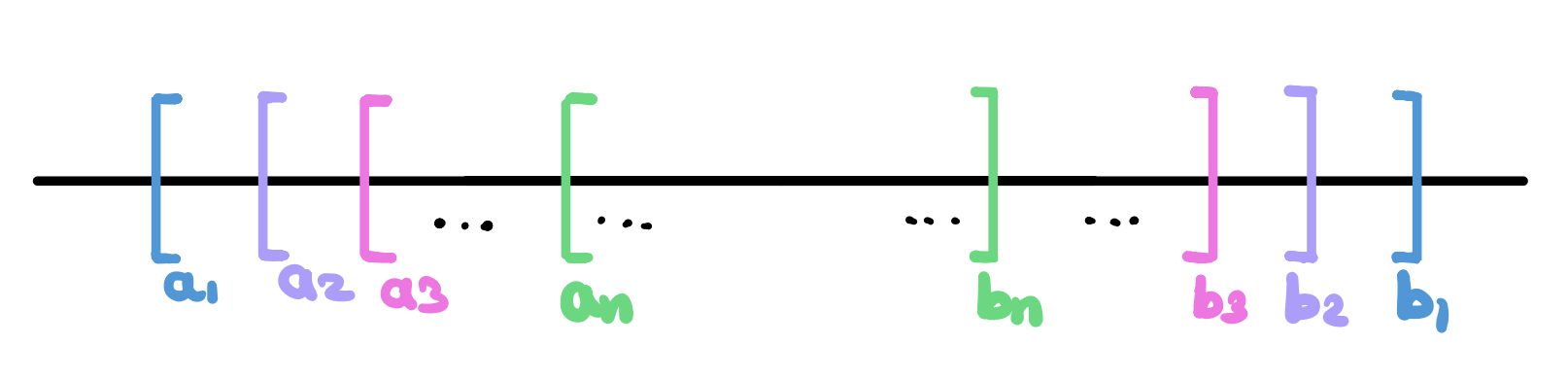
Consider the sequence \((a_n)\) of all left end points of each interval. This sequence is increasing and bounded above by \(b_1\). Therefore, by the Monotone Convergence Theorem, the limit exists and it is equal to the supremum of \((a_n)\). Similarly, consider the sequence \((b_n)\) of all right end points of each interval. This sequence is decreasing and bounded below by \(a_1\). Therefore, by the Monotone Convergence Theorem, the limit exists and it is equal to the infimum of \((b_n)\). Now, let

$$ \begin{align*} \lim\limits_{n\to\infty} a_n = \sup a_n = a \quad \text{ and } \quad \lim\limits_{n\to\infty} a_n = \inf b_n = b \end{align*} $$

But we also know that \(a_n \leq b_n\) for all \(n \in \mathbb{N}\). Then by the Comparison Theorem, we know that \(a \leq b\). But this implies that

$$ \begin{align*} a_n \leq a \leq b \leq b_n. \end{align*} $$

Hence, the intersection

$$ \begin{align*} \bigcap_{n=1}^{\infty} I_n = [a,b]. \end{align*} $$

Moreover, we are given that the length of the interval \(I_n = b_n - a_n \to 0\) as \(n \to \infty\). Then

$$ \begin{align*} \lim_{n\to\infty} b_n - a_n &= 0\\ \lim_{n\to\infty} b_n - \lim_{n\to\infty} a_n &= 0 \quad \text{(By the Algebraic Limit Theorem)} \\ b - a &= 0 \\ b &= a. \end{align*} $$

Therefore, the intersection contains a single point as desired. \(\ \blacksquare\)

References