I thought this was a really cool example so here it goes: Evaluate the following:
To do this, we’ll need to relate a few quantities that are bigger and smaller than \(\sin(x)/x\). Let’s start:
The Area of the Triangle $$ABC$$
Suppose we have the following triangle \(ABC\) inside the unit circle.
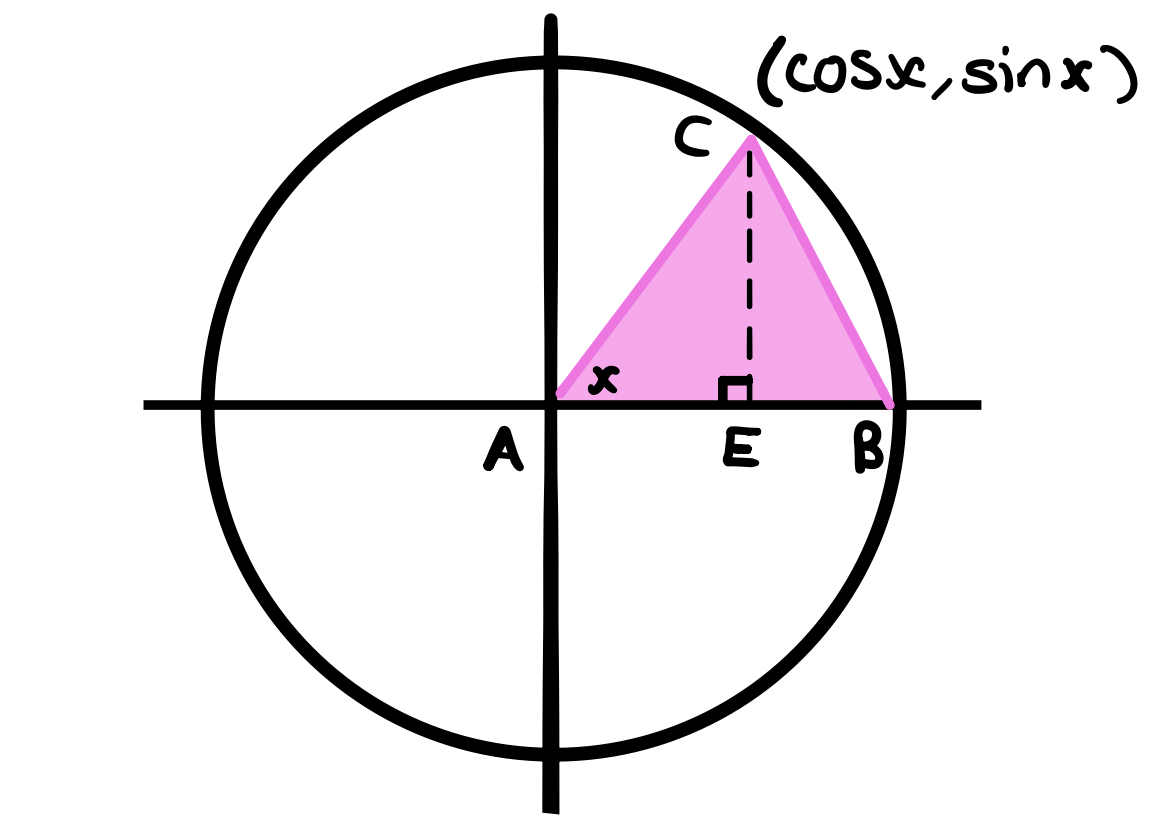
We know the area of a triangle is,
where \(b\) is the length of the base and \(h\) is the height of the triangle. Since this is a unit circle then \(b = AB = 1\) because the radius of the unit circle is 1 by construction.
What about the height? The height is \(CE\). What is \(CE\)? If we look at the smaller triangle, we’ll see \(\sin(x) = \frac{opp}{hyp} = \frac{CE}{1} = CE\). So the height is just \(\sin(x)\).
So the area of the pink triangle \(ABC\) is therefore,
The Area of the Sector $$ABC$$
Now we want to calculate the area of the following shaded sector,
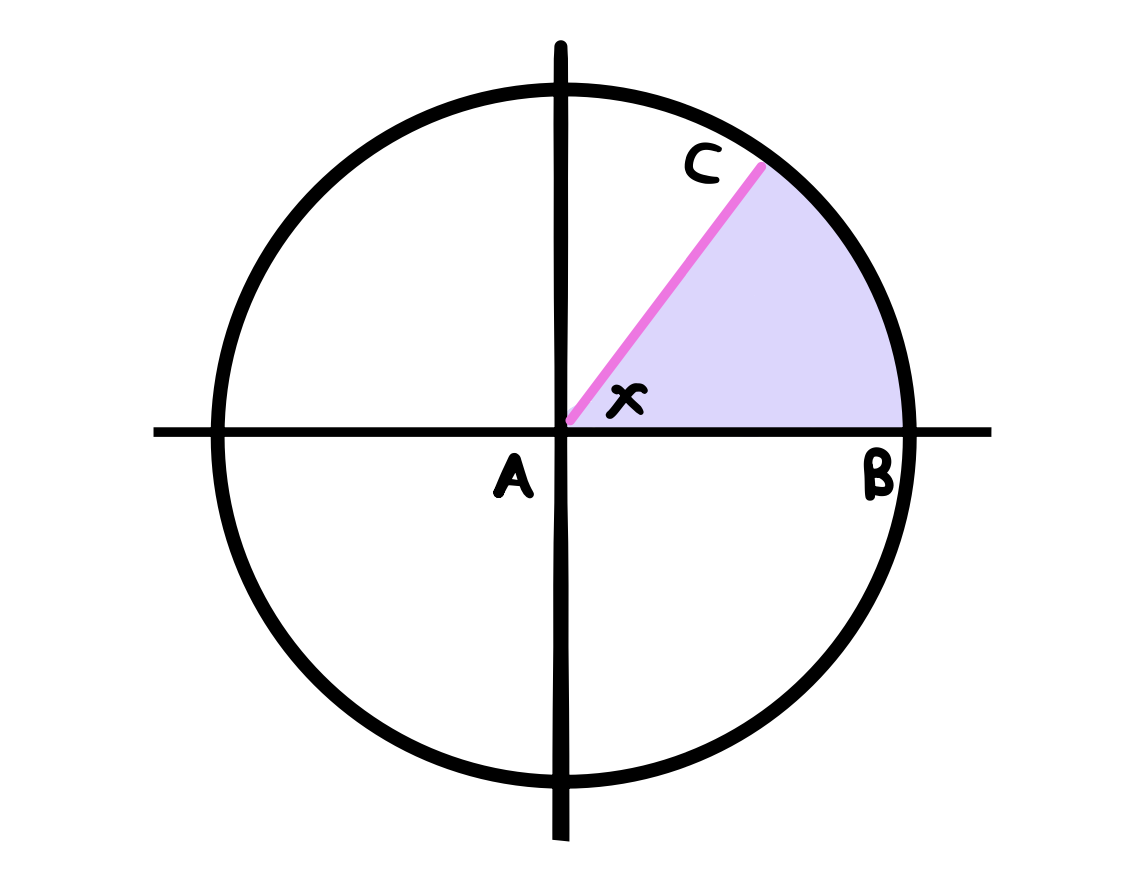
The area of the sector is
The Area of the Triangle $$ABD$$
The last area we’re interested in is the area of the biggest (extended) triangle,
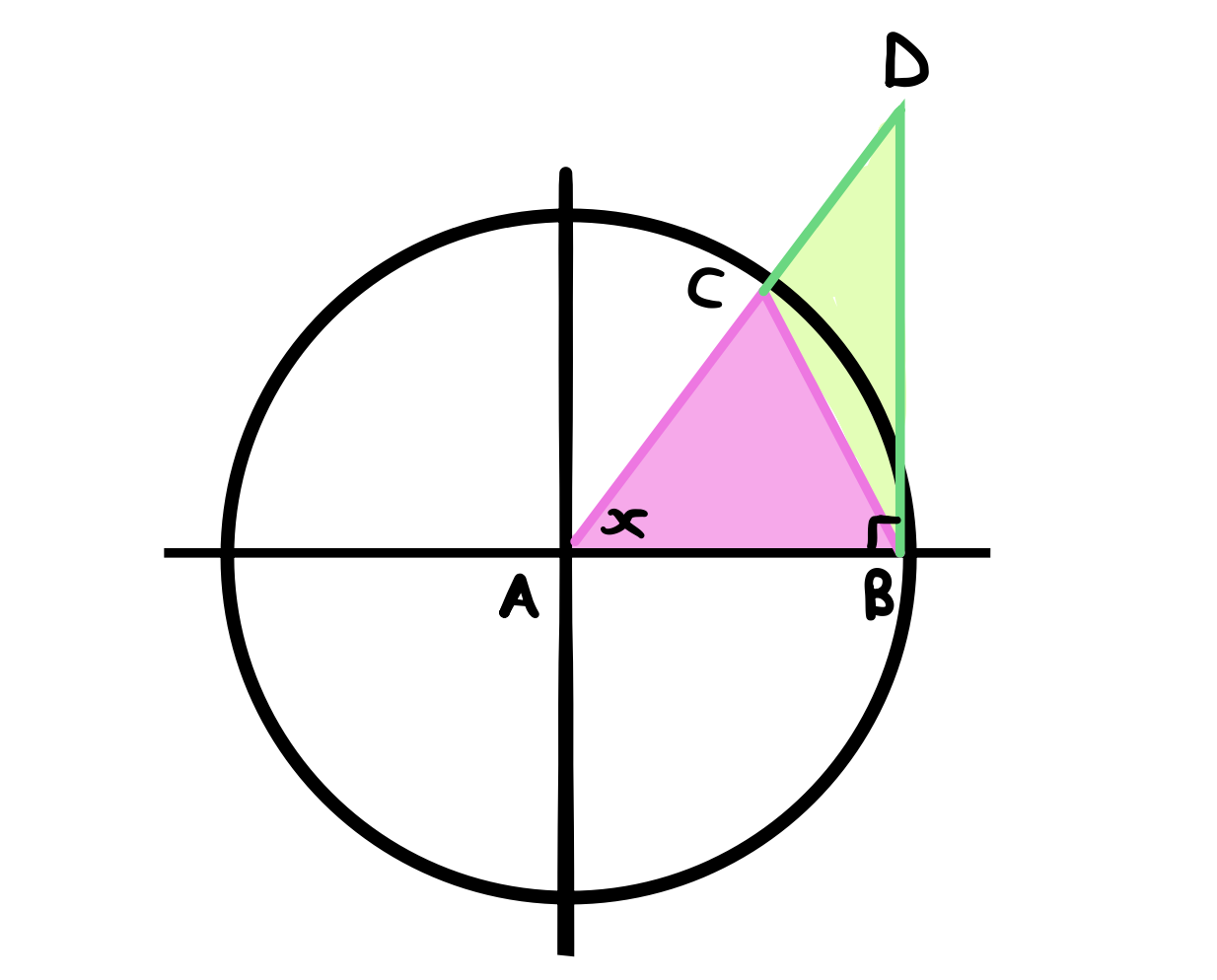
Again, we know the area of a triangle is
We established earlier that the base \(AB\) is 1. What about the height? The angle \(\angle ABD\) is a right angle by construction so \(DB\) is equal to the height of the triangle. What is \(DB\)? We can’t use \(\sin(x)\) like last time because we don’t know anything about the length of \(AD\). However we do know the length of \(AB\) and one way to relate \(AB\) and \(DB\) together is through \(\tan(x)\). So,
The length of the bigger triangle \(ABD\) is therefore,
Finding the Limit

Looking back at the areas of the triangles and sector, we know that the area of the biggest triangle must be greater than the area of the sector and the area of the sector is greater than the area of the smaller triangle (proof?). Using this we can write the following inequality,
We can further simplify and also divide by \(\sin(x)\). Note here that \(sin(x)\) is postive,
If we. try to find the limit as \(x\) goes to 0 of the first and last term we will find that
Similarly we can also find the limit of the last term here
We can now use the Squeeze Theorem to conclude that
And that’s what we wanted to find!
References: