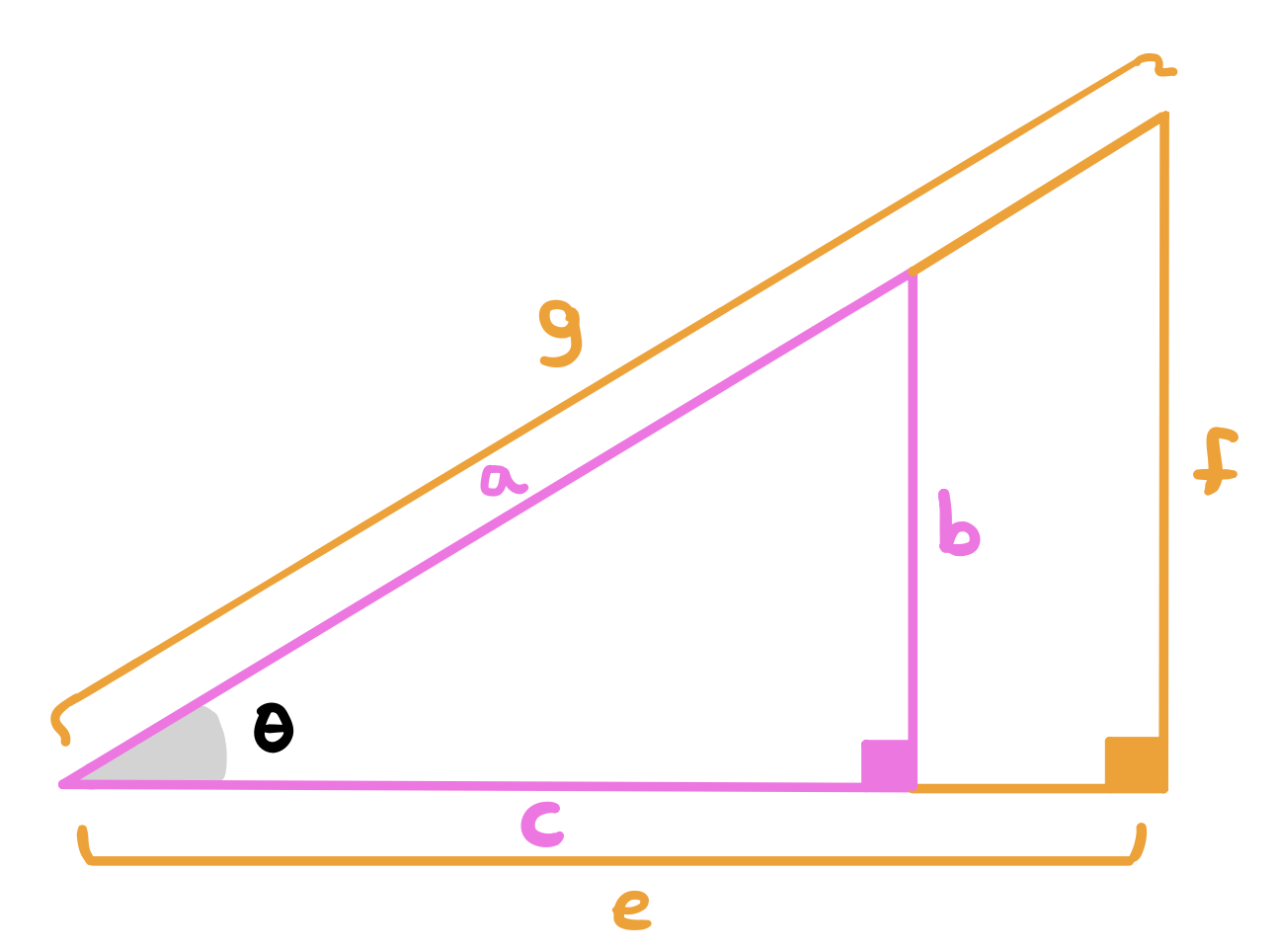
Given the pink right angle triangle above, the sine of \(\theta\) is defined to be the ratio of the length of the side opposite \(\theta\) to the length of the longest side of the triangle (the hypotenuse). The cosine of \(\theta\) is defined as the ratio of the length of the side adjacent to \(\theta\) to the length of the longest side in the triangle (the hypotenuse).
If we extend this triangle to be a bigger similar triangle (keeping \(\theta\) fixed). These two triangles must be similar. Why? Because we fixed \(\theta\) and we have a right triangle in each triangle. Having a pair of equal angles makes the two triangles similar, meaning that the ratios of their corresponding sides will be the same. Therefore, the \(\sin\) and \(\cos\) values will stay the same.
The Unit Circle
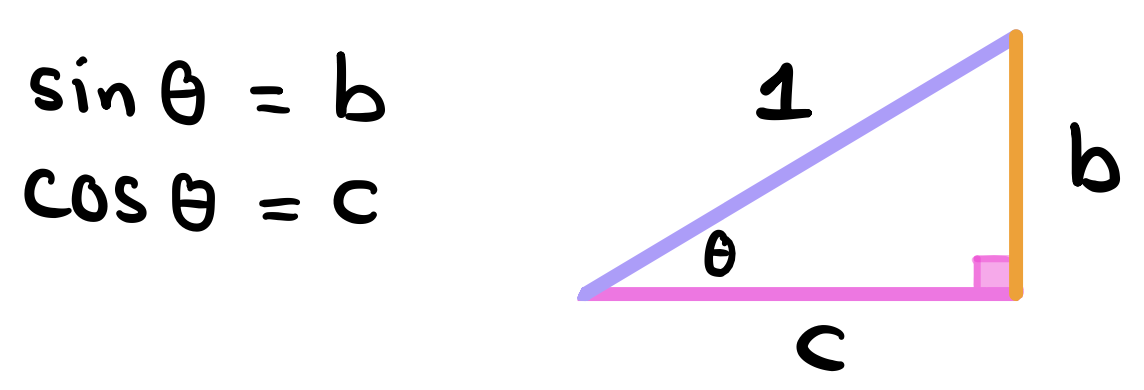
So now we know that if we fix \(\theta\), whatever right triangle we come up with will be similar to the original triangle, meaning that \(\sin(\theta)\) and \(\cos(\theta)\) will always be the same. Since it doesn’t matter how big this triangle is, then why not just let the hypotenuse be 1 to make it easy to calculate these values. Setting the hypotenuse to 1 will lead to having \(\sin(\theta)\) become just \(b\) and \(\cos(\theta)\) become just \(c\) since we don’t need to divide by \(r\) because \(r\) is just 1! Neat!
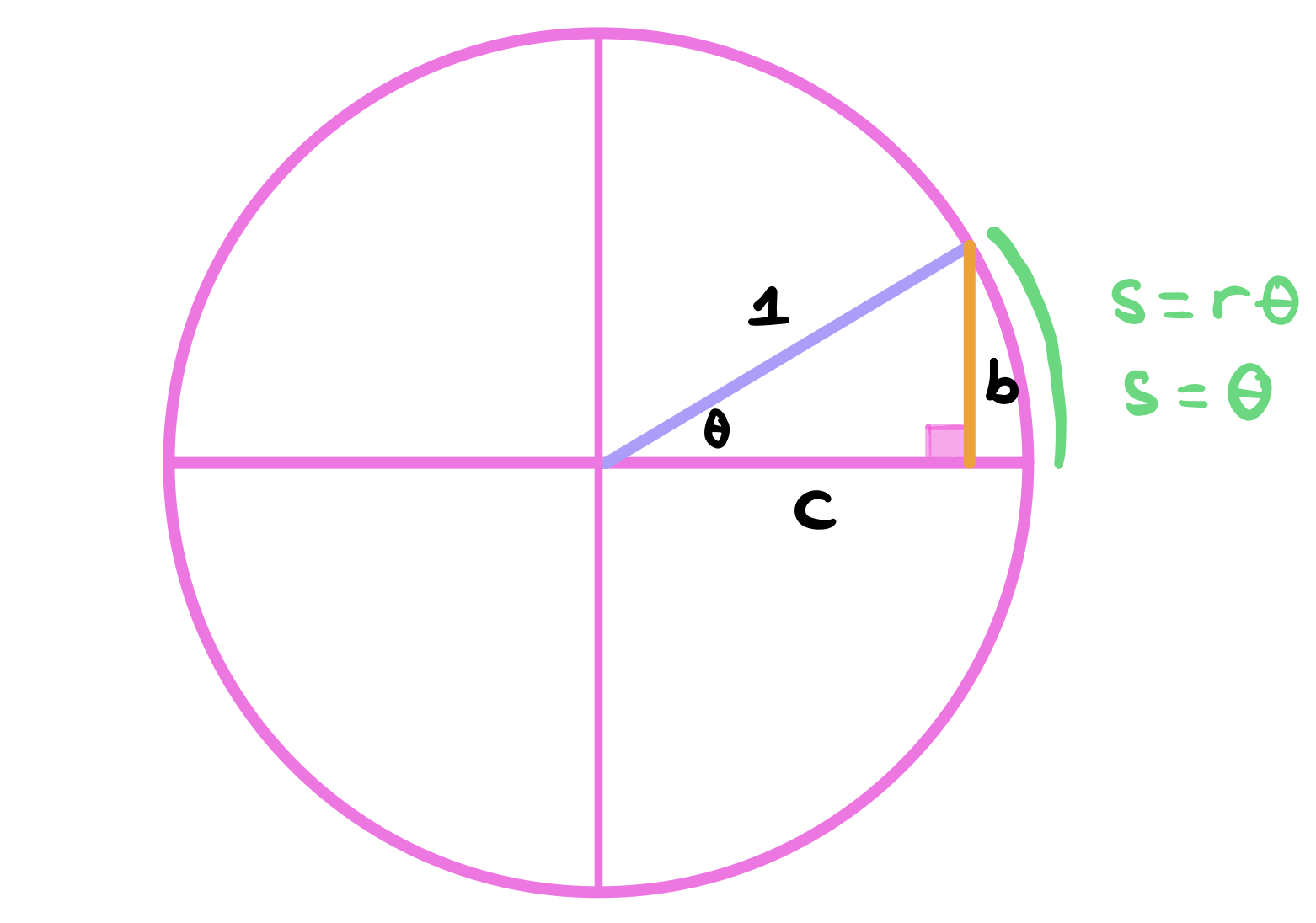
Next, Let’s make the hypotenuse of this triangle be the radius of a circle. This circle is a called a unit circle since the radius is 1. Notice here that the arc length formed by \(\theta\) is now exactly the value of \(\theta\). Another neat thing. This comes from the fact that the arc length is \(\theta\) multiplied by the radius but we know the radius is 1 and so the arc length is just the value of \(\theta\).
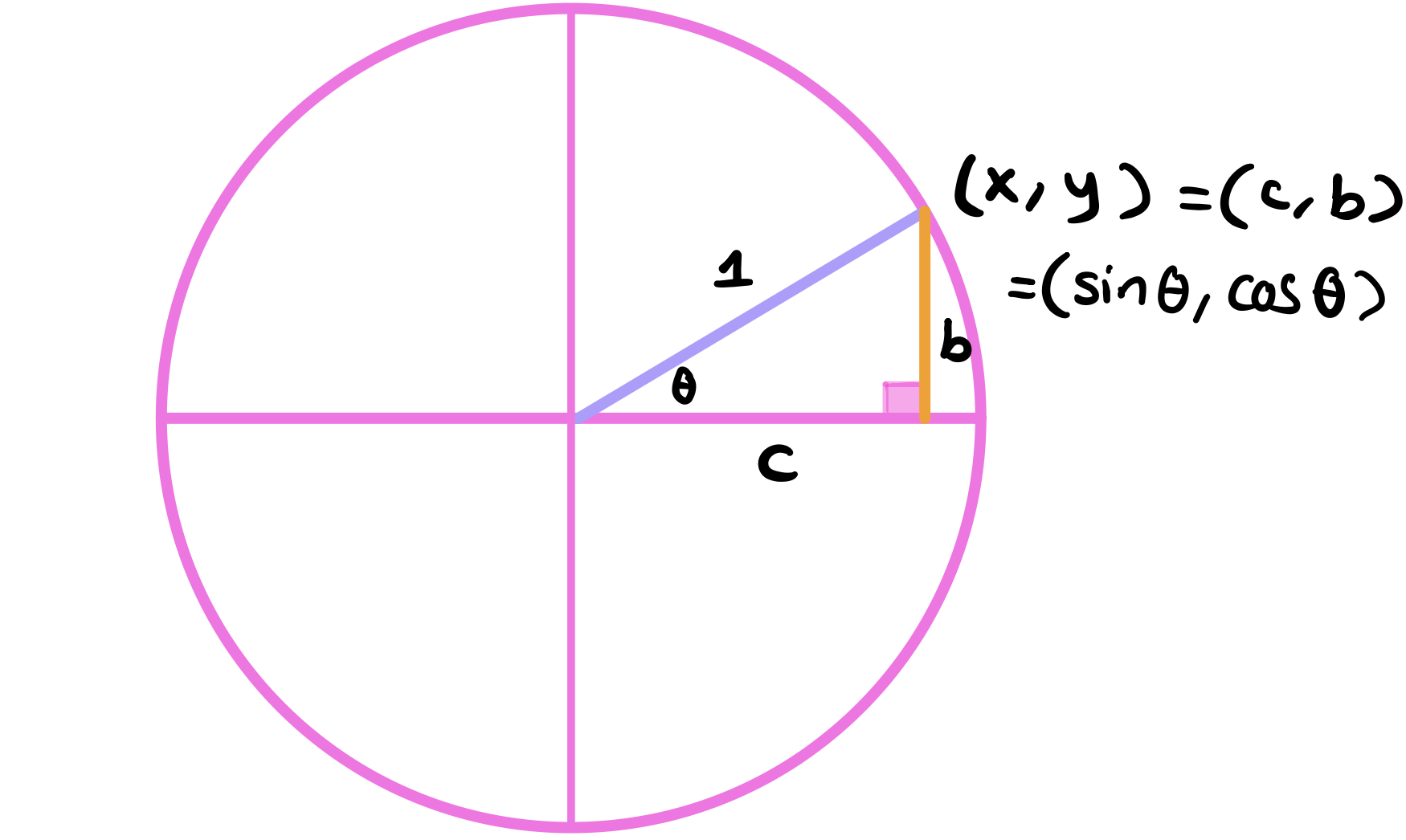
Also, note that the coordinates of that point at the end of the arc is just \((b,c)\) which can also be written as (\(\sin(\theta)\), \(\cos(\theta)\)). Very cool!
The Unit Circle Expanded
So now we know that the coordinates \((x,y)\) on the unit circle are exactly the trigonometric functions \((sin(\theta), cos(\theta))\). We also know that \(\sin(\theta)\) represents the relationship between the opposite side and the hypotenuse. We chose to work with the unit circle because it’s easy to compute these trigonometric functions when the radius is 1 and no matter what radius we choose, these trigonometric functions will be exactly the same so why not just pick a radius that’s easy.
Since we often work with right triangles and need to calculate these trigonometric functions, often you’ll see them pre-computed for a bunch of famous angles. The following is taken from Wikipedia where it shows some of these famous angles and their precomputed coordinates/trigonometric functions.

References: