Suppose we want to graph the following function.

$$ \begin{align*} \frac{x^2-x-1}{x+1} \end{align*} $$

How can we approach this?

Vertical Asymptotes

The first step is finding the asymptotes. For the vertical asymptote, we want to find what makes the denominator equal to zero. none of the factors of the numerator will be \((x+1)\) so we don’t need to worry about simplifying further since nothing will cancel out. We can then just solve,

$$ \begin{align*} x + 1 &= 0 \\ x &= -1 \end{align*} $$

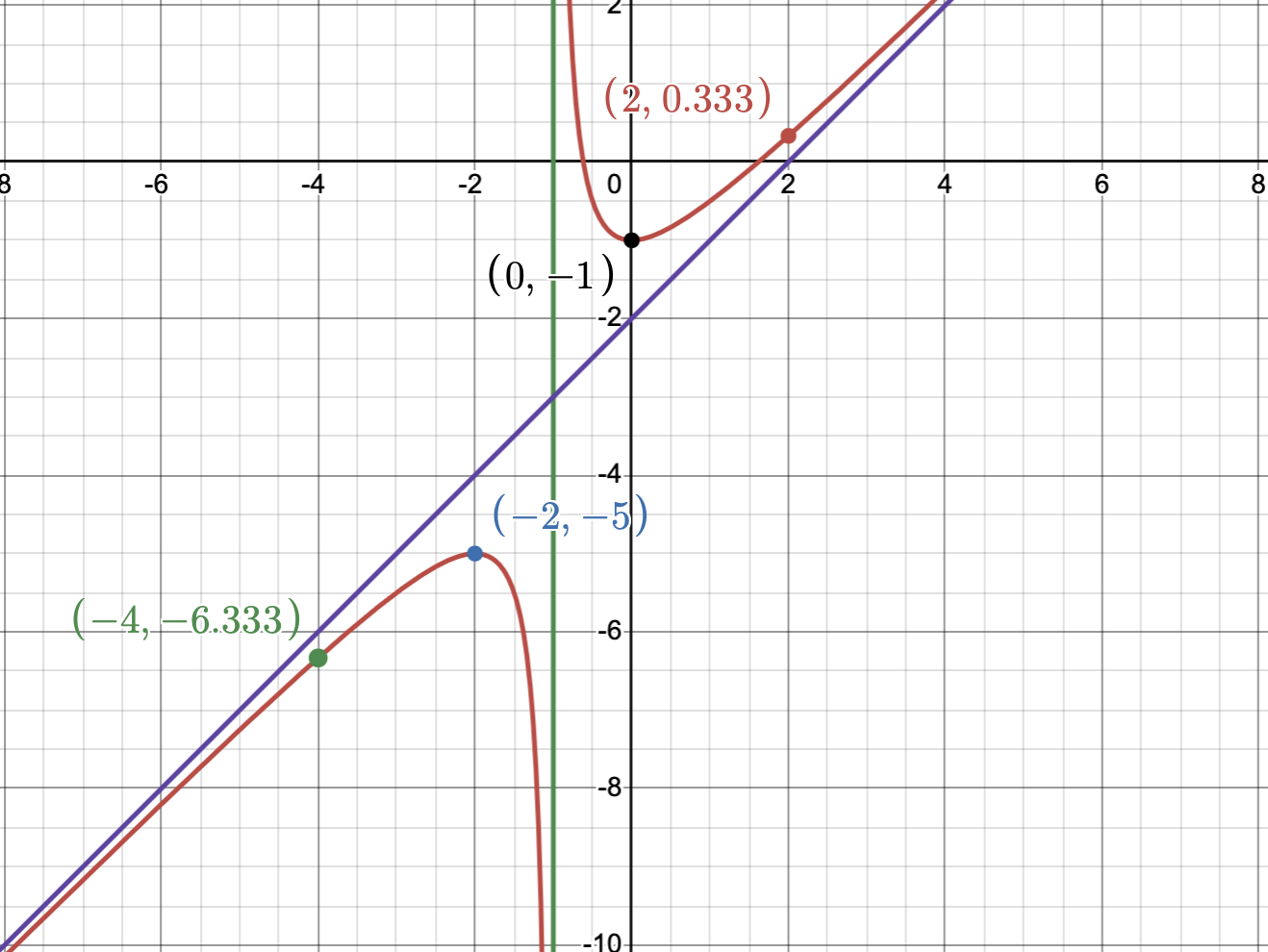
So \(x = -1\) will be our vertical asymptote.


Horizontal Asymptotes

Next, we need to find the horizontal asymptote. Let’s revise the three cases we did before. Suppose we have the function

$$ \begin{align*} \frac{a_m x^m + a_{m-1} x^{m-1} + ...}{a_n x^n + a_{n-1} x^{n-1} + ...} \end{align*} $$

Then,

  • if \(m < n\), then the horizontal asymptote is \(y = 0\).
  • if \(m = n\), then the asymptote is the leading coefficient of the numerator over the leading the coefficient of the denominator. \(\frac{a_m}{a_n}\).
  • if \(m = n + 1\), we will not have any horizontal asymptotes and instead we will have a slanted asymptote.

Here, \(m = n + 1\), therefore, we don’t have a horizontal asymptote and in fact we have a slanted one.

Slanted Asymptotes

To find the slanted asymptote, we divide \(x^2 - x - 1\) by \(x + 1\). We’ll get \(x-2\) plus \(\frac{1}{x+1}\). We don’t care about the remainder since as \(x\) get large numerically (whether negative or positive), this term will be zero. The slanted asymptote therefore will happen at \(x - 2\).


Plotting points for each section of the graph

After graphing the asymptotes, we'll have the following graph,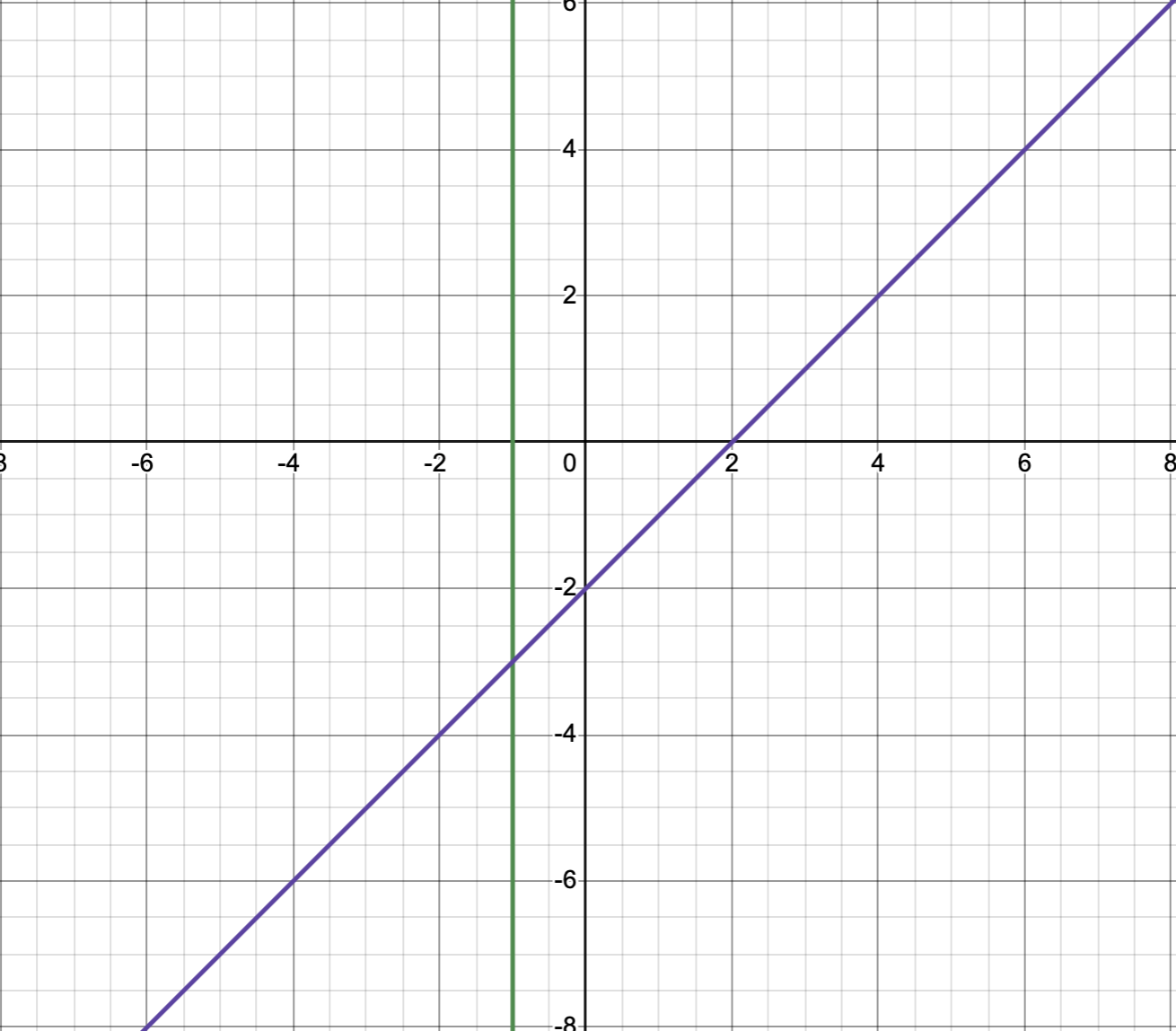

Now, we want to find at least two points to plot for each section of the graph. Let's find the value of \(f\) for example at at 0 and 2. We can see that \(f(0) = \frac{0 - 0 - 1}{0 + 1} = -1\) and \(f(2) = \frac{4 - 2 - 1}{2 + 1} = -5\). For the other side, let's find $$f$$ at values \(-2\) and \(-4\). \(f(3) = \frac{4 + 2 - 1}{-2 + 1} = -5\) and \(f(5) = \frac{16 + 4 - 1}{-4 + 1} = -\frac{19}{3}\). And now we're done!


References: