Suppose we want to graph the following function.
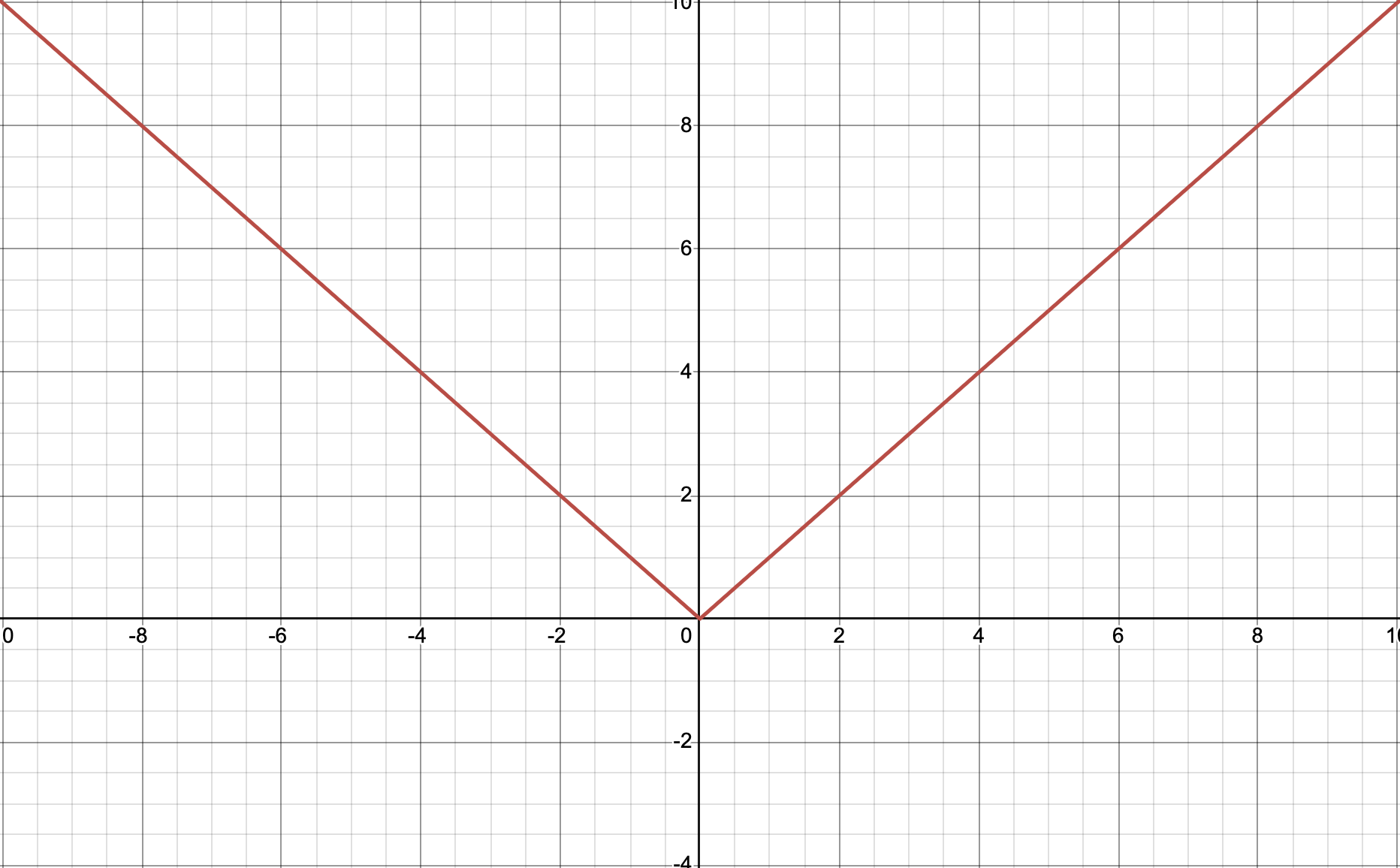
There are a couple of ways to approach this but it’s good to keep in mind what the simplest absolute value function looks like. So \(f(x) = \lvert x \rvert\). We know we can plot a few points and then we’ll get
Finding the New Vertex
If you take a look at the graph of \(\lvert x \rvert\), you’ll notice that all we need to know is really the vertex of that \(v\) shape in the graph we want to plot. Once we figure out this new vertex, then we can just choose a point on each side of the new vertex and draw straight lines. To find the new vertex, we’ll take a look at the standard form which is
The \(x\)-value of the new vertex happens to be the value that would make \(x - b\) above equals to zero. In our case we have \(x + 4\) inside the absolute value.
So the new vertex has an \(x\) value of \(-4\). To find the \(y\)-value of the new vertex, we can just evaluate the function at this \(x\)-value. So for \(x = -4\), we will have,
So now that we have the new vertex at \((-4,-5)\). We can choose points before and after this vertex and plot the new graph. For example \(f(-3) = -3\) and f(-5) = -3$$. We can then draw straight lines and get the following,
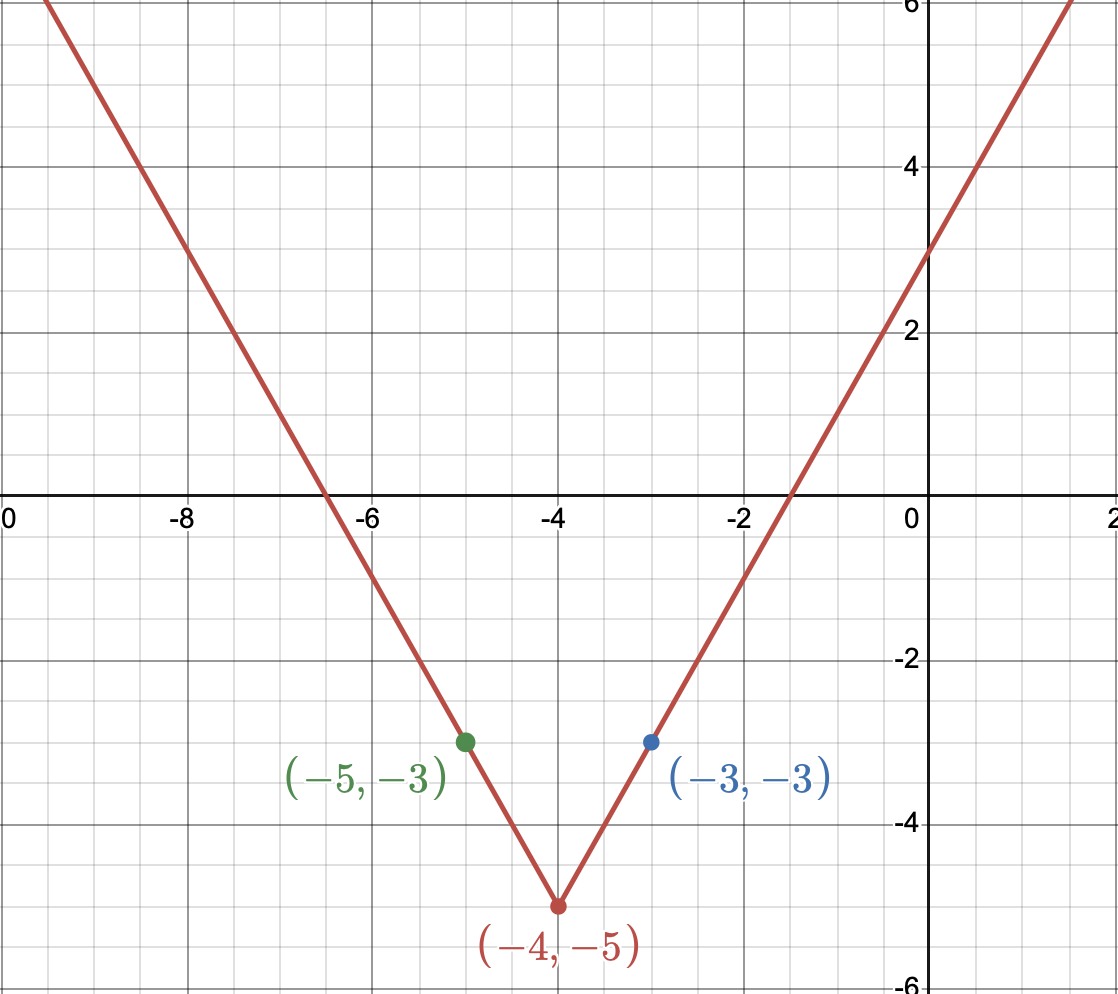
Transforming the simplest function
We can also approach this in a different way. We know the simplest absolute value function is just \(\lvert x \rvert\) and we know we want to graph \(2 \lvert x + 4 \rvert - 5\). So let’s trasform \(\lvert x \rvert\) to \(2 \lvert x + 4 \rvert - 5\).
Starting with \(\lvert x \rvert\), we know the vertex is at \((0,0)\). We also know that we have the points \((1,1)\) and \((-1,1)\) that satisfy the function. Next, we’ll apply the following transformations to transform the points to satisfy the new function instead.
- We introduce the stretching factor $$2\lvert x \rvert$$. This stretching factor will transform the points to $$(0,0), (1,2), (-1,2)$$. Note that the vertex remains unaffected by stretching.
- Next, we introduce the horizontal shift factor $$+4$$ inside the absolute value. So now our function is $$2\lvert x + 4\rvert$$. This factor will shift the graph to the left by 4 points (to the left because the standard form has $$x - b$$). So now the points will transform to $$(-4,0), (-3, 2), (-5, 2)$$.
- Finally, we want to vertically shift the graph by the factor $$-5$$ so 5 steps down. So the previous points will change to $$(-4,-5), (-3, -3), (-5, -3)$$

So we arrived at the same exact function just in a different way.
References: