Suppose we want to graph the function $4\log_2(x-3)+1$. How can we approach this?

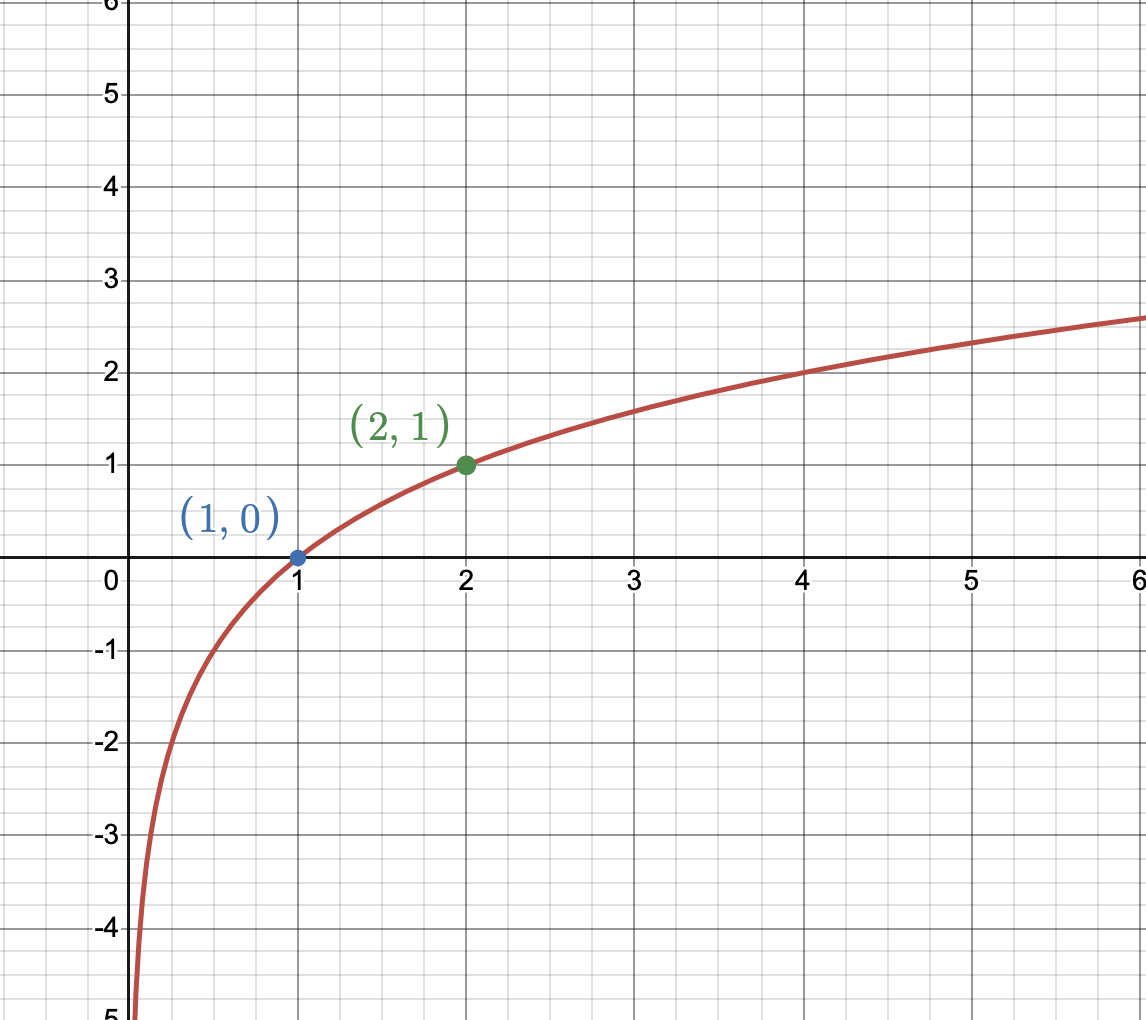
We can first simplify the problem by studying the function $f(x) = log_2(x)$. We know that its domain is all $x$ values where $x \geq 0$. We can also see here that as $x$ approaches $-\infty$, the function $f$ approaches 0 but never really reaches there. There isn’t a value of $x$ that would make $\log_2(x)$ be zero. Therefore $f$ has a vertical asymptote at $x = 0$. This asymptote plus a few other points that we can plug in like $f(1) = 0$ and $f(2) = 1$ can help us graph $f$ below.

But what we want to graph is $g$. Let’s re-write $g$ in terms of $f$ below,

$$ \begin{align*} g(x) &= 4f(x-3) + 1 \end{align*} $$

So taking $f(x) = \log_2(x)$, we just need to apply some transformations to get to $g$.

Stretching or Shrinking Vertically

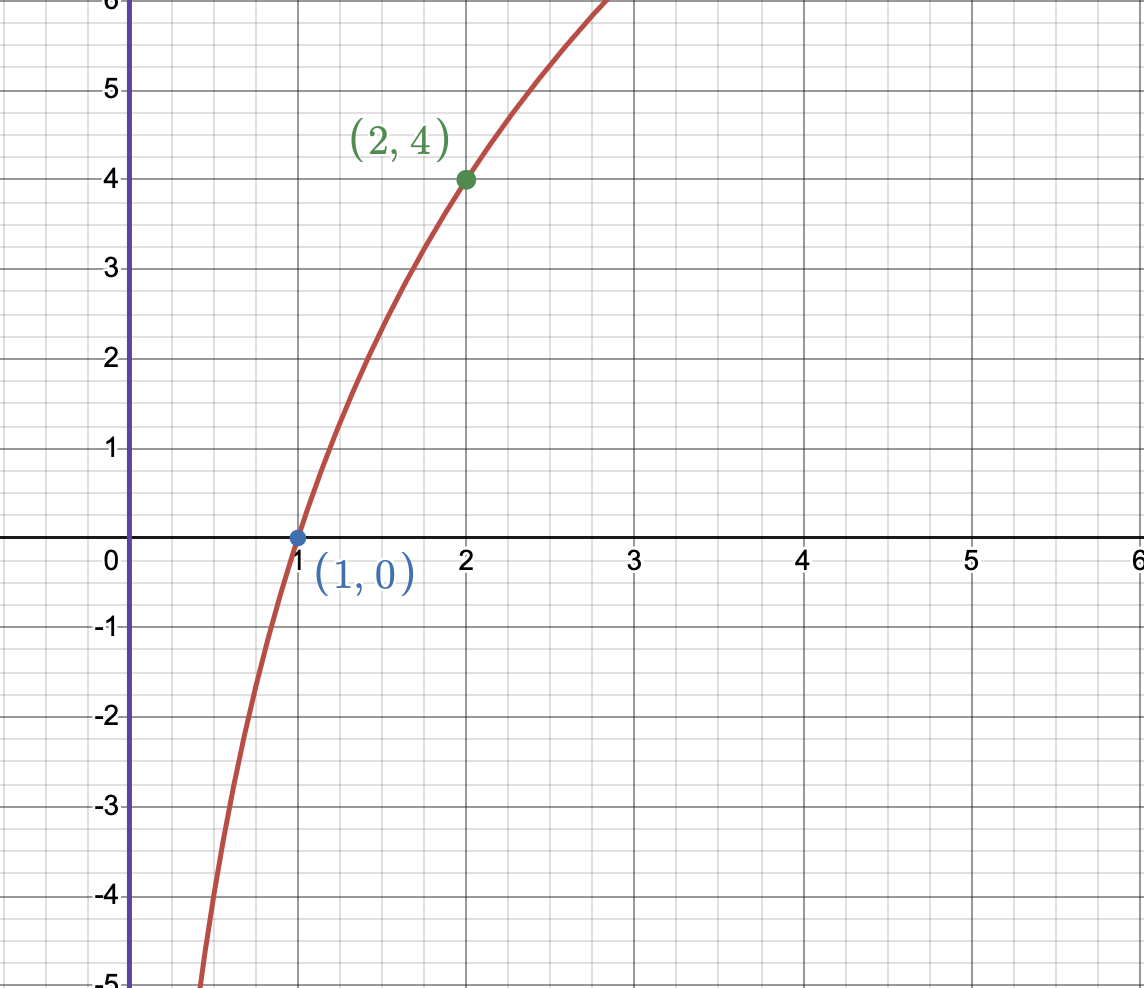
Let’s sketch the $f$ after adding the stretching factor 4 (it will shrink if the factor was negative). So now we have $4f(x)$. This means that $f(1)$ is $0(4) = 0$. and $f(2)$ is $1(4)=4$. The asymptote won’t get affected! Let’s sketch the graph with the new points $(1,0)$ and $(2,4)$ below.

Shifting Left or Right Horizontally

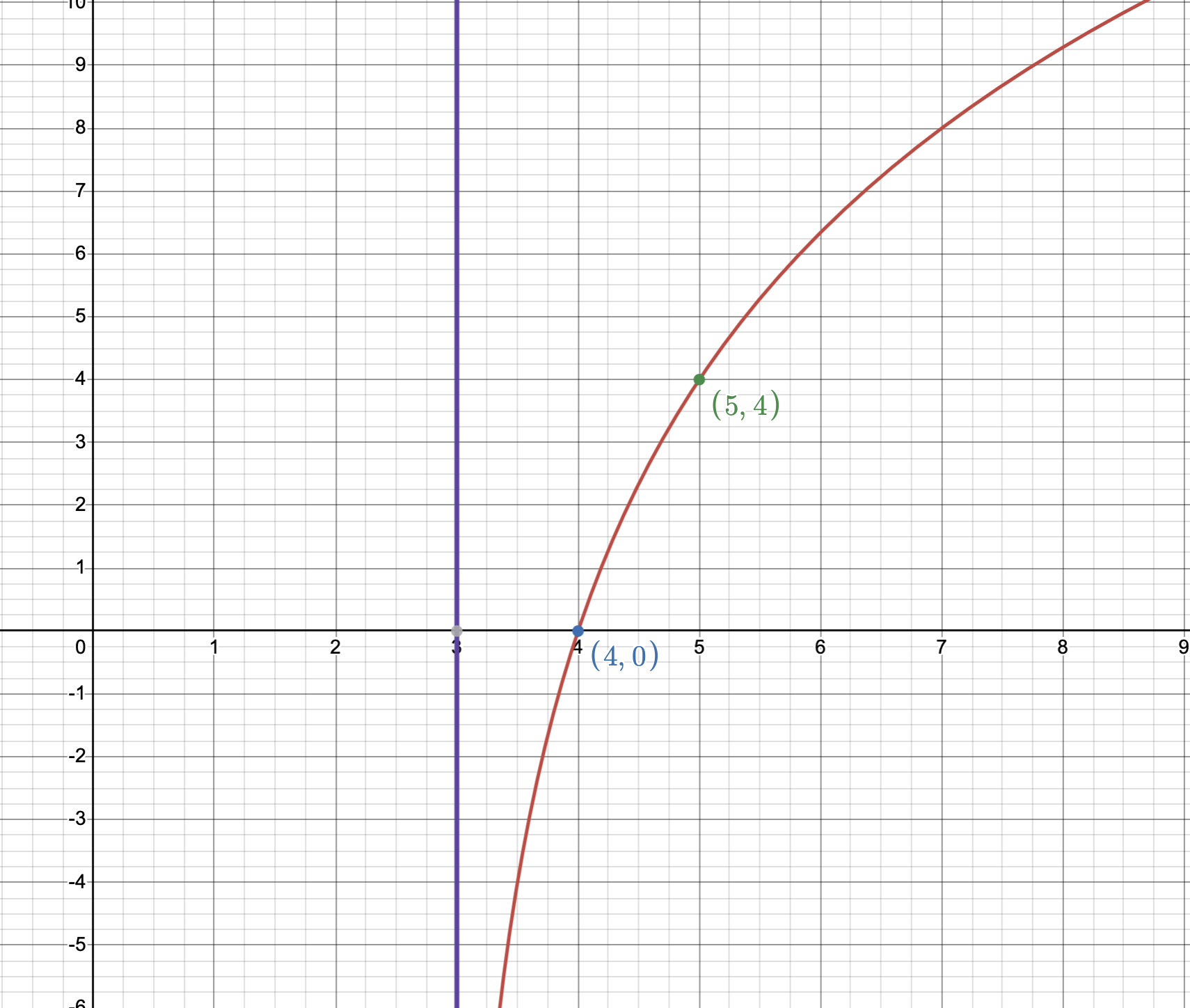
Next, let’s add the inside term -3 so that $f$ is now $4f(x-3)$. This means that we need to shift the graph horizontally to the right by 3 points. So $f(1+3=4) = 0$ and $f(2+4=5) = 4$. Shifting a graph horizontally will translate the asymptote as well so now the asymptote will be at $x = 3$. Let’s sketch the new asymptote along with the new points $(4,0)$ and $(5,4)$.

Shifting Up or Down Vertically

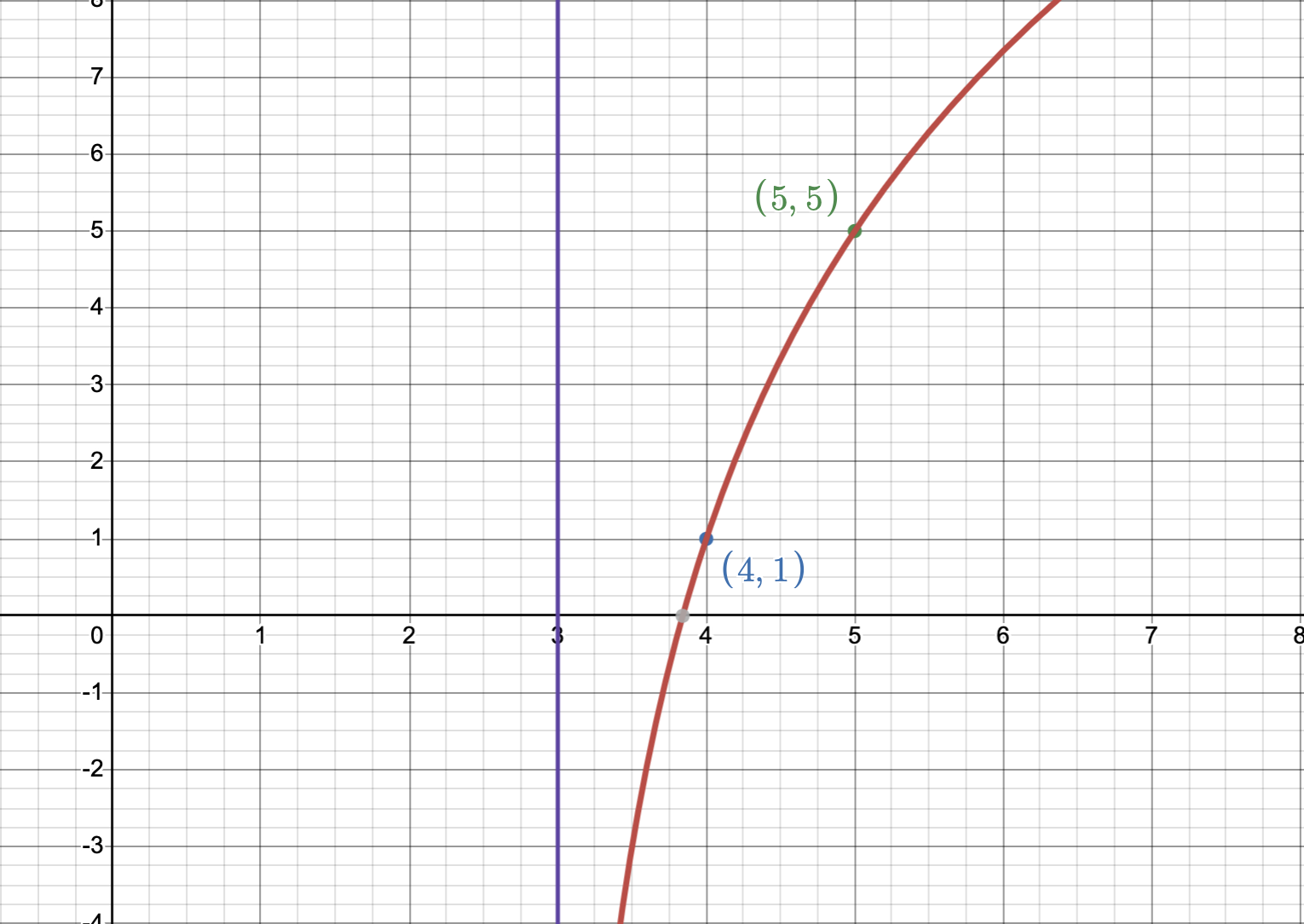
Finally we want to add the term +1 so that $f = 4\log_2(x-3) + 1$. This shifts the function vertically up by 1 point. So the point $(4,0)$ will be $(4,1)$ and the point $(5,4)$ will be $(5,5)$. The asymptote is unaffected since this is a vertical shift. Finally, this will be the final graph!

References: