I really liked this idea from the reference video at the bottom of the page. Basically, if we’re given some angle like \(\theta = \frac{5\pi}{6}\) and we want to find out for example \(\cot(\theta)\), we can approach this by seeing that the denominator is \(6\) and so we can divide the upper half of the unit circle into 6 equal parts. Upper half only because \(\frac{5\pi}{6} < \pi\)!
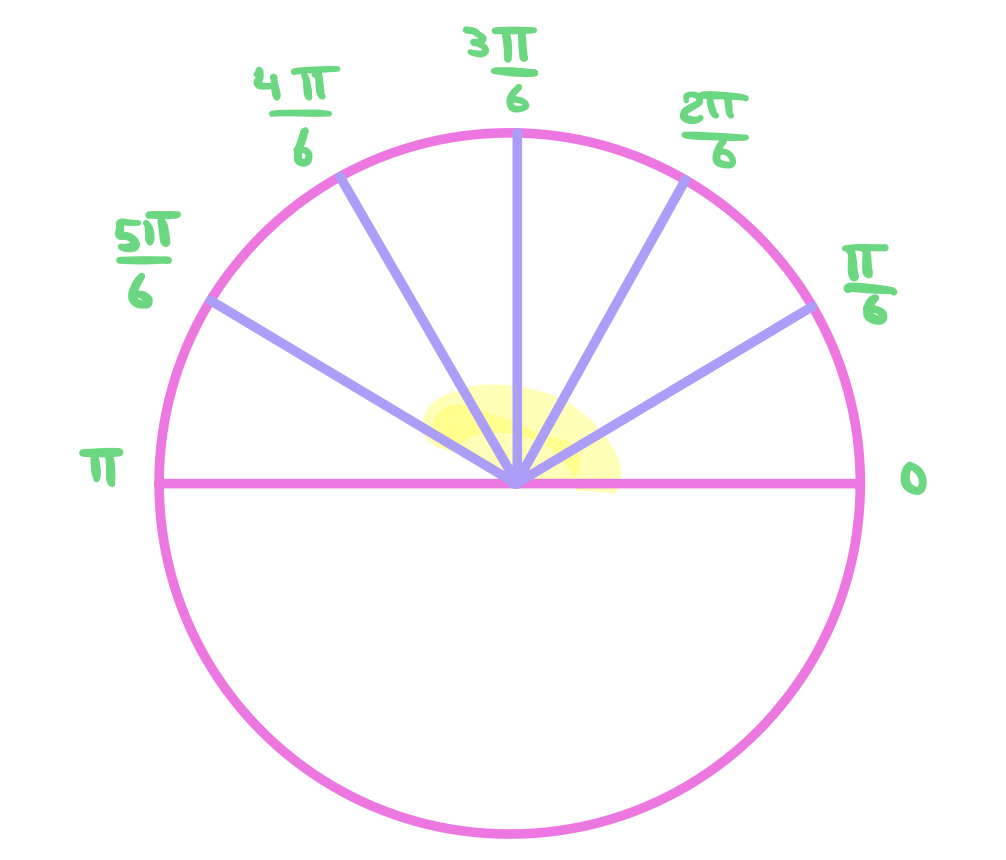
We’re interested in the 5th part since we want \(\frac{5\pi}{6}\). The point corresponding to the angle \(\frac{5\pi}{6}\) has the same y-coordinate of the point corresponding to \(\frac{\pi}{6}\). It also has the same magnitude of the x-coordinate but the sign is negative.
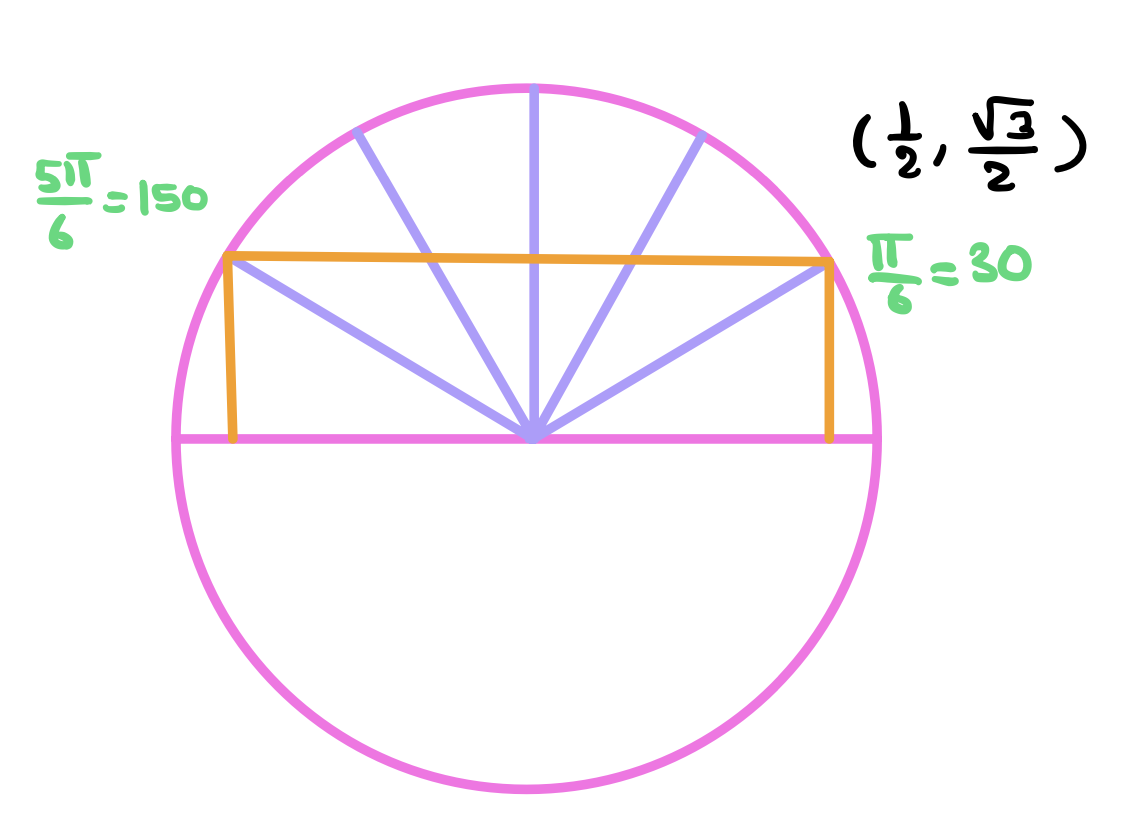
The coordinates of the point at angle \(\frac{\pi}{6}\) are \((\frac{1}{2}, \frac{\sqrt{3}}{2})\) and so the coordinates of the point at \(\frac{5\pi}{6}\) will be \((-\frac{1}{2}, \frac{\sqrt{3}}{2})\).